S P F A —差分约束 \color{0000FF}{SPFA—差分约束} SPFA—差分约束
功能:
- 求不等式的可行解
- 求最大值与最小值(重点)
(一)不等式的可行解 \color{92D050}{(一)不等式的可行解} (一)不等式的可行解
步骤:
- 将每个不等式 x i ≤ x j + c k x_i\le x_j + c_k xi≤xj+ck,转化为一条从 x j x_j xj 到 x i x_i xi 的一条长度为 c k c_k ck 的边
- 找到一个超级源点,使得该源点一定可以遍历到所有边
- 从源点求一遍单源最短路
无解情况: 负环 \color{0000FF}{负环} 负环
(二)最大值与最小值(指每一个变量的最值) \color{92D050}{(二)最大值与最小值(指每一个变量的最值)} (二)最大值与最小值(指每一个变量的最值)
结论:
若求最小值,则选择最长路;若求最大值,则选择最短路
存在性:
满足有至少一个条件 x i ≥ c x_i\ge c xi≥c 或 x i ≤ c x_i\le c xi≤c,其中 c c c 为常数,保证了最值,否则就是相对的大小,无最值
问题1:如何转化 x i ≤ c x_i\le c xi≤c,其中 c c c 为常数
方法:建立一个超级源点( 0 0 0 号点),并创建 x 0 ∼ x i x_0\sim x_i x0∼xi 的一条边,长度为 c c c 即可文章来源:https://www.toymoban.com/news/detail-638098.html
问题2:结论的证明
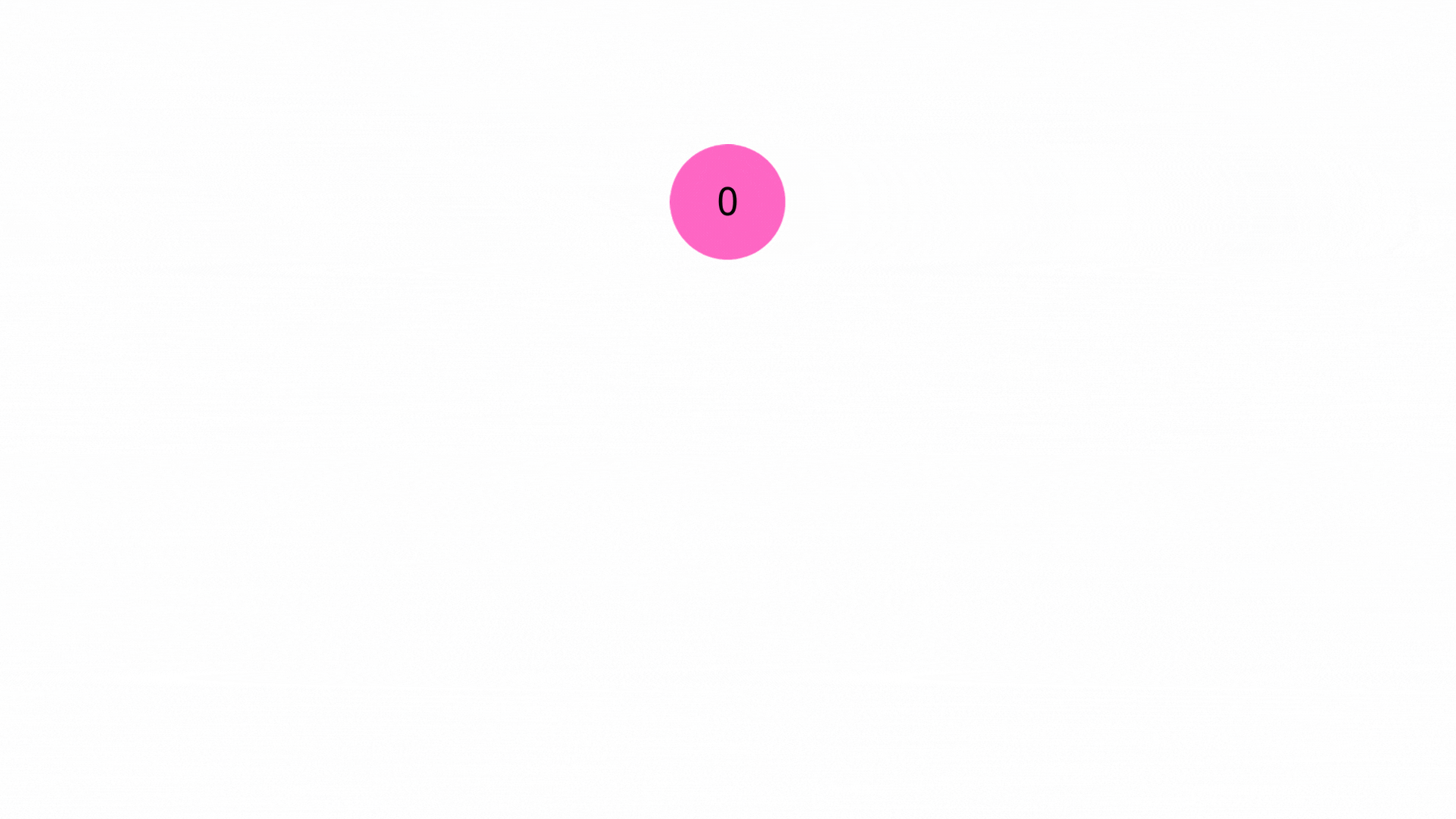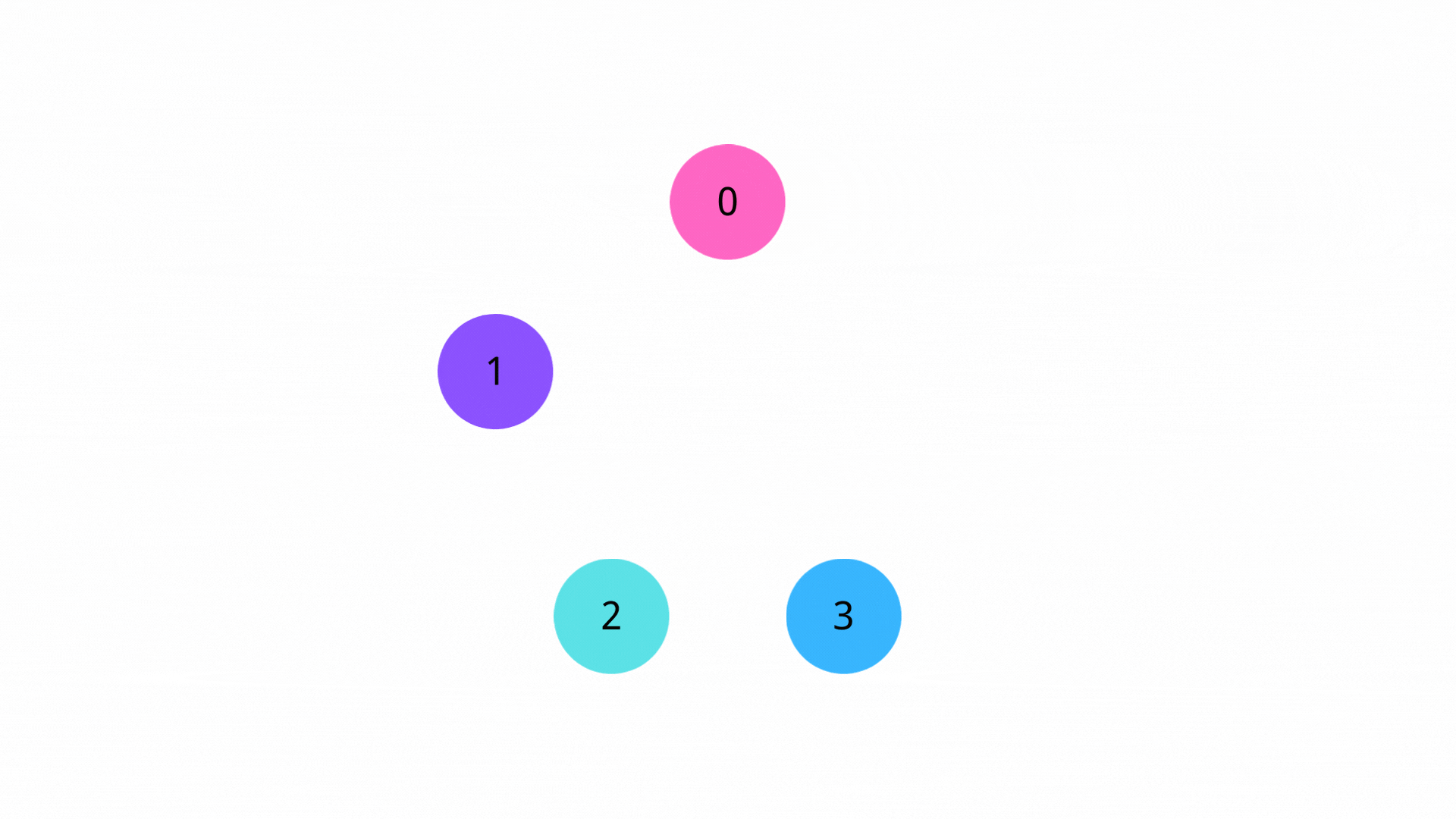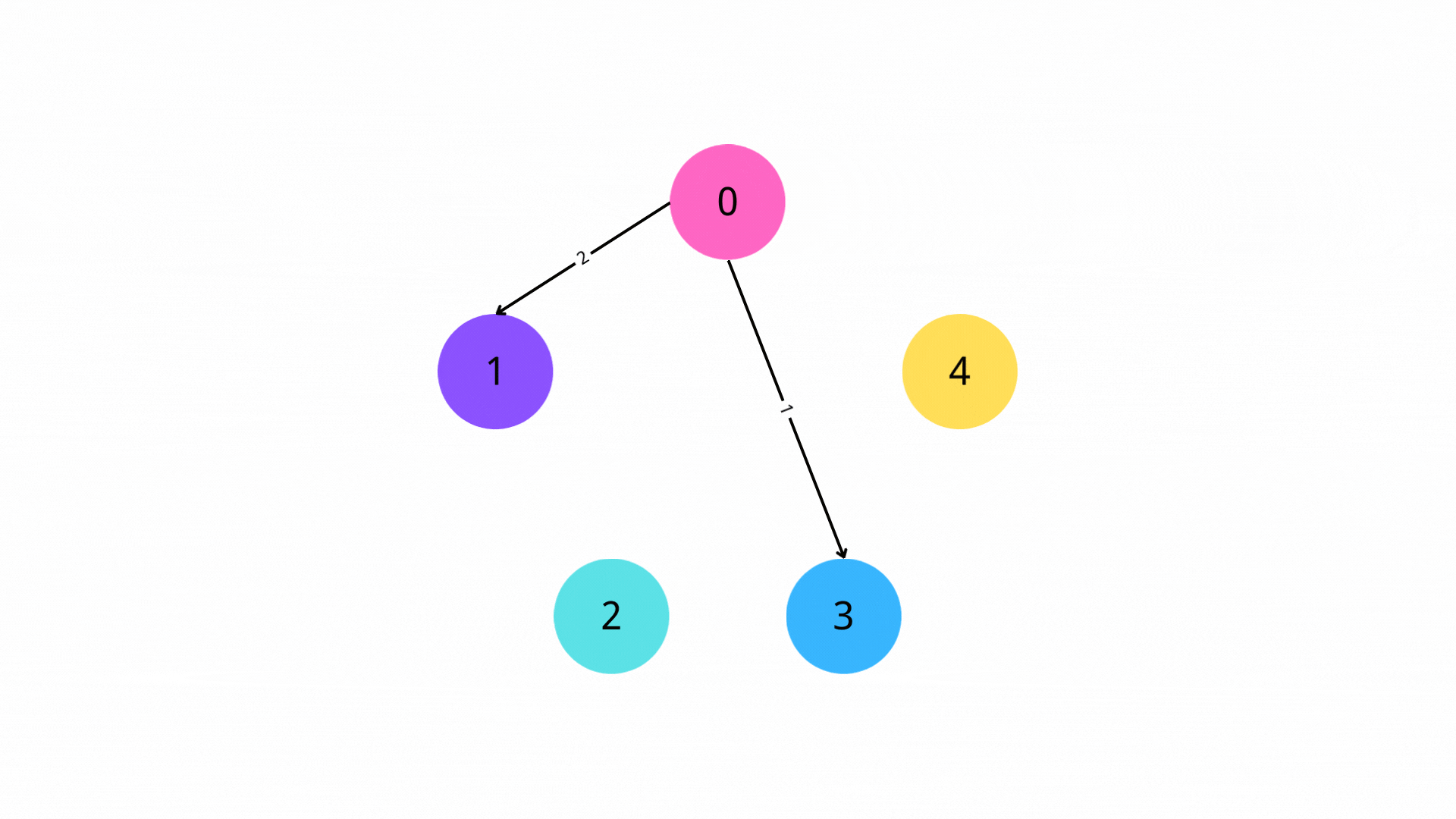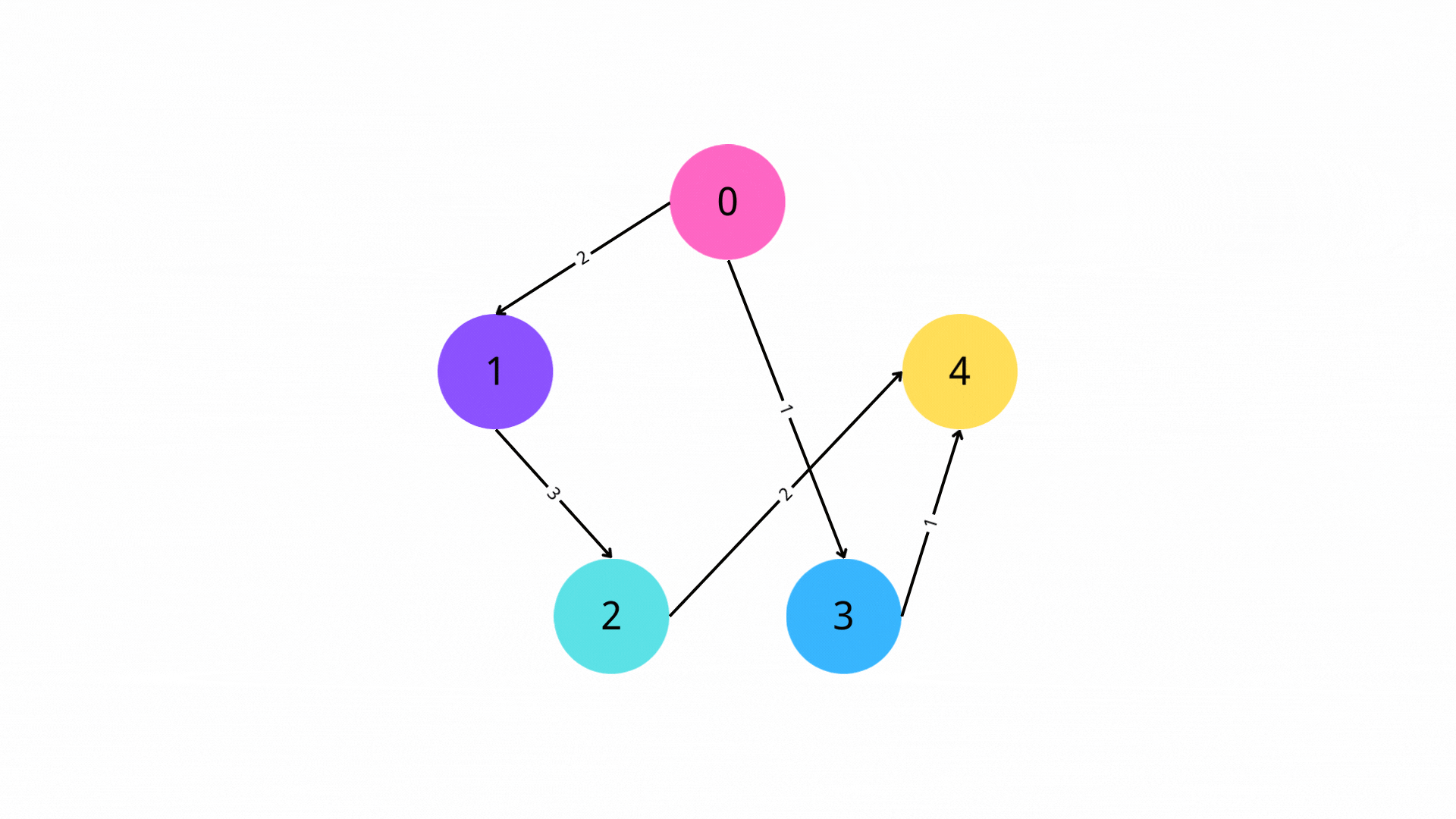
以最大值为例:求出所有从 x i x_i xi 出发,构成的不等式链 x i ≤ x j + c 1 ≤ x k + c 1 + c 2 ≤ ⋯ ≤ c 1 + c 2 + c 3 + … x_i\le x_j + c_1 \le x_k + c_1 + c_2\le\dots\le c_1+c_2 + c_3 + \dots xi≤xj+c1≤xk+c1+c2≤⋯≤c1+c2+c3+…,计算出所有的上界, x i x_i xi 的最大值即为所有上界的最小值,故选用最短路。文章来源地址https://www.toymoban.com/news/detail-638098.html
到了这里,关于SPFA之差分约束的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!