【图的深度优先遍历】输出DFS序列-Toy模板网

这篇具有很好参考价值的文章主要介绍了【图的深度优先遍历】输出DFS序列。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

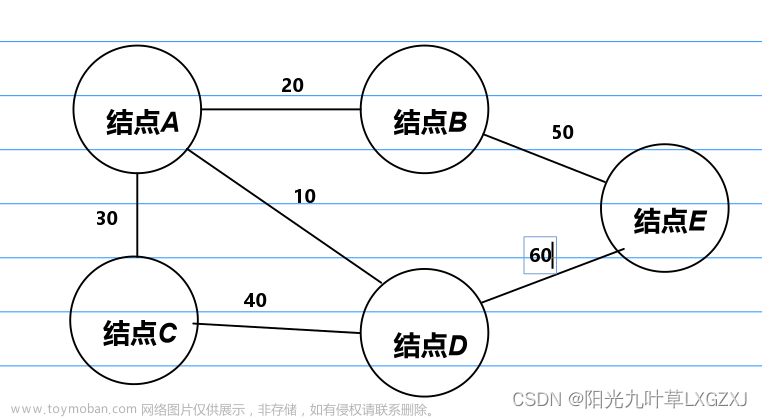
算法思想：

能走就必须走，不撞南墙不回头。
①随便从一个点开始走
②随机选择一条边走，只要这个点还能往下走的话，就一定要往下走不能回头，每个点只能走一次
③当这个点走不动之后再回溯，回溯到之前的点看看还有没有别的边没走

注意：

①判重：
不管是dfs还是bfs，一定要记得判重，即每个点只能走一次，不能重复走
②dfs序列
dfs序列（又叫深度优先遍历序列）：到达（访问），每个点的顺序称为DFS序列
区别：
到达顺序：在递归开头遍历——>dfs序列
回溯顺序：在递归结尾遍历——>拓扑排序
③图的连通性：
dfs要注意图的连通性问题，图可能不连通，所以一定要枚举所有点，如果没搜过的话
而bfs一般不需要考虑图的连通性问题，因为不影响他的答案

画图理解：

dfs代码输出,数据结构,深度优先,算法,图论,数据结构,dfs 文章来源地址https://www.toymoban.com/news/detail-639206.html

代码实现：

#include <iostream>
using namespace std;
const int N=100010;

struct Node{
    int id;//节点编号
    Node *next;//next指针:下一个节点的地址
    
    Node(int _id): id(_id),next(NULL){}
}*head[N];

/*
邻接表：每个点都用一个单链表来存，所以需要开一个n个链表的头结点

*head[maxn]的意思：
这里相当于是一个装头节点的的指针数组.
比如与结点邻近有三个结点2、3、4,那么h[1]表示结点1邻近所有结点的链表，
即h[1]表示结点1周围邻近节点的单链表的表头， 1 -> 2 -> 3 -> 4，其中2、3、4顺序随意。
h[1]到h[n]分别表示了每个结点的邻近结点的情况，即每个h[i]都对应一个链表。
所以需要加星号表示这个数组中存放的是Node* 类型的数据

*/


int n,m; //n个点m条边
bool st[N];//判重数组，标记这条边是否出现过


//头插法邻接表建图
void add(int a,int b)
{
    Node *p=new Node(b);//创建一个点，点的编号是b
    p->next=head[a];
    head[a]=p;
}


void dfs(int u)
{
    st[u]=true;//注意①：dfs需要判重：因为每个点要保证只能走一次，不能重复走
    printf("%d ",u);//注意②：输出dfs序列：dfs序列是指到达每个点的顺序，要在递归开头遍历（即循环前输出）
    for(Node *i=head[u];i!=NULL;i=i->next)//枚举u的所有邻边
    {
        int j=i->id;//邻边的编号
        if(!st[j])//如果这一点没有搜过
            dfs(j);//继续往下搜
    }

}


int main()
{
    scanf("%d %d",&n,&m);
    while (m -- )
    {
        int a,b;
        scanf("%d %d",&a,&b);
        add(a,b);
    }
    
    for(int i=1;i<=n;i++)//注意③：dfs需要注意图的连通性，有的图可能不联通，所以dfs一定要枚举一遍所有点
    {
        if(!st[i])//如果这个点没有搜过的话
            dfs(i);//就从这个点开始在搜一遍
    }
    
    return 0;
}