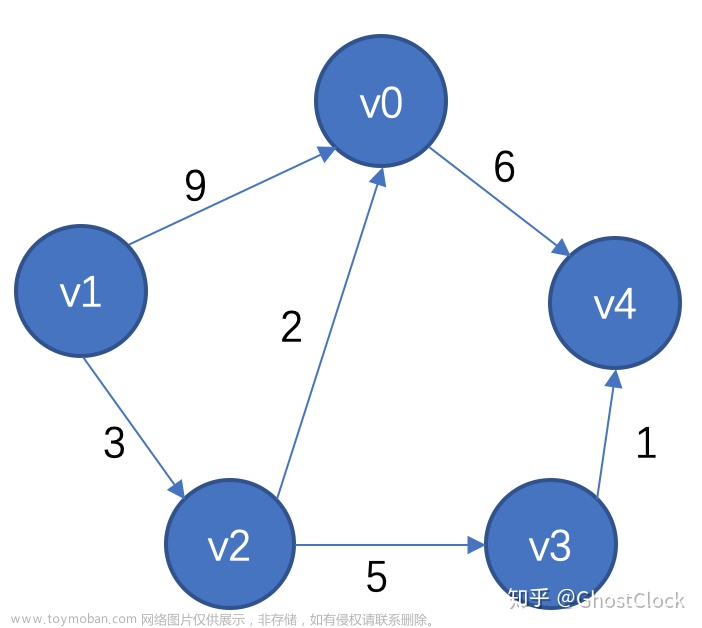
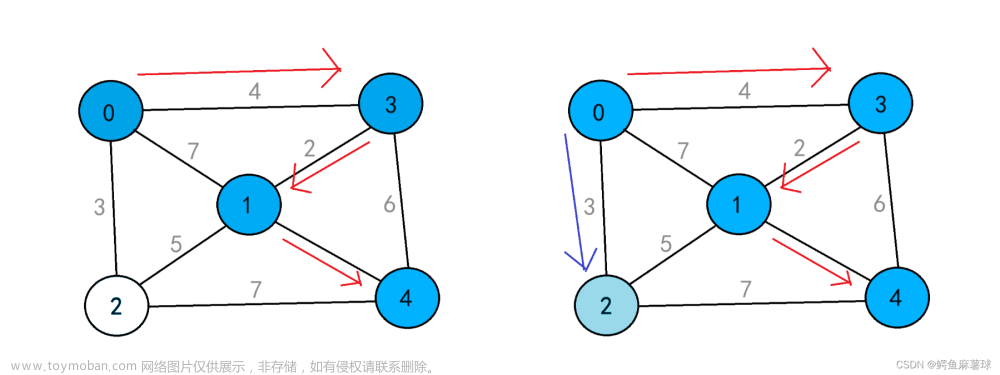
1、BFS和DFS介绍
深度优先搜索(DFS)和广度优先搜索(BFS)是一种用于遍历或搜索树图的一种算法,在这个过程中保证图或数的每个结点被访问且仅被访问一次,再按照每个结点访问的顺序不同分为深搜和广搜。
本文只讨论这两种算法在搜索方面的应用!
1.1深度优先搜索算法
深度优先搜索(Depth-First-Search,DFS)它沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
这个算法可以用递归实现也可以用栈实现。使用递归很容易理解而且代码量较少,当然它也有缺点,就是对规模较大的图或数使用递归思路会导致栈溢出。目前阶段我都会使用递归去实现深搜。
1.2广度优先搜索算法
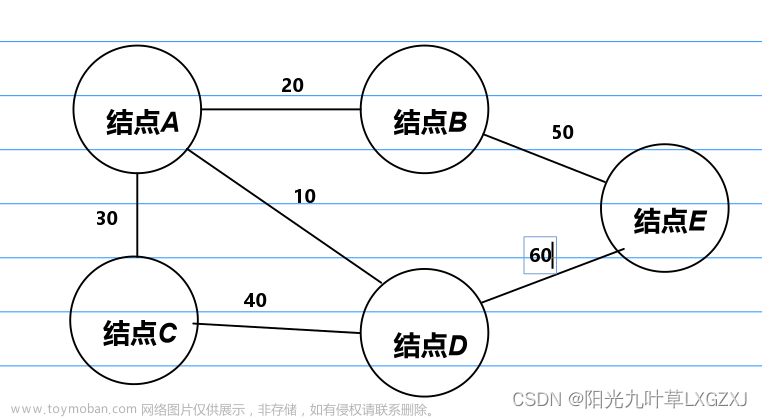
广度优先搜索(Breadth-First-Search,BFS)这个算法很好理解,直观的解释它就像一个炸弹爆炸时那种层层推进的搜索方式,是要当前结点周围的结点符合搜索条件,那么就同步地将当前结点周围的结点作为源节点继续宽搜,直到找到目标结点为止。
这个算法独特的搜索策略就决定了它的最终搜索结果一定是最优解!所以目前只要我看到有最优解要求时,我会毫不犹豫的选择BFS。
1、BFS和DFS的经典应用
起初我认为DFS只有在特定的情况的情况才有最优解,但是if语句确实万能,通过对这个语句的灵活运用,DFS依旧可以实现最优解(虽然意义不大。因为BFS的实现更简单,而且时间复杂度更低!)。
1.1迷宫问题应用
1.1.1原始版
问题描述:现给出一个30*50的迷宫矩阵(见代码),其中标记1为障碍物,0为可以通行的地方。迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这 个它的上、下、左、右四个方向之一。请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中 D<L<R<U。分别代表下、左、右、上。
在这个问题中 首先我们用DFS求解,对于最优解,DFS处理方式如下:
if(pos>best)//如果当前路径已经走的步长pos大于之前最短补偿best
return;//就不需要沿着现有路径继续走下去了,这个剪枝可以加快速度
if(x==row && y==col)
{//已经到达终点
string temp;
for(int i=0;i<pos;i++)
temp+=a[i];
if(pos<best)//将更短的路径记录下来
{
ans=temp;
best=pos;
}
else if(pos==best && temp<ans)
ans=temp;
return;这段代码是递归的终止条件,注意每当我们探索到一个结点时都会有这个方案从起点到这个的步数pos,那么通过比较每个方案的当前pos就可以把路径上所有节点都存储从起点到这个位置的最小步数,那么当有新方案时,若其pos大于已经存储的最小步数best就可以直接抛弃这个方案了。这样当我们所有方案都探索完时,就得到从起点到终点的最小步数了。
对于字典序,我们只需要控制在深搜时优先探索方向顺序为下、左、右、上即可。
DFS解法完整代码如下:
#include <iostream>
#include <cstring>
using namespace std;
//4行6列
const int row =30;
const int col =50;
const int marc=50;
int best; //从起点到终点的最小步数
int mins[marc+5][marc+5];
//以左上角第一个位置为终点,往下x方向,往右y方向
int maze[row+1][col+1]=
{
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
1,0,1,0,1,0,1,0,1,0,0,1,0,1,1,0,0,1,0,0,1,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,1,0,1,0,
1,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,1,0,1,0,0,1,0,1,
1,0,1,1,1,1,0,1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,1,1,0,0,0,0,0,0,0,1,0,0,0,0,
1,0,1,0,0,0,0,0,0,0,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,1,
1,0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,0,1,0,0,0,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0,
1,1,1,0,0,1,0,0,0,1,1,0,1,0,1,0,0,0,0,1,0,1,0,1,1,0,0,0,1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,0,1,1,1,
1,0,0,0,1,1,0,1,1,0,1,0,1,0,1,0,0,1,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,0,0,0,
1,1,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,1,0,0,1,1,0,0,0,0,1,0,0,0,0,1,1,1,0,1,0,
1,0,0,1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,0,0,0,0,1,0,0,1,
1,1,1,0,0,0,1,1,0,1,0,0,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0,
1,0,0,0,1,0,0,0,0,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,1,0,1,0,0,0,1,0,1,0,1,0,1,0,0,0,0,1,0,1,
1,1,1,1,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,0,0,1,0,0,0,1,0,1,0,0,
1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,1,1,0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,0,1,0,1,0,1,0,0,0,1,1,
1,1,0,1,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,1,0,0,1,1,1,1,0,1,1,0,1,0,0,0,0,1,0,0,0,
1,1,0,1,0,1,0,1,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,1,1,0,1,1,1,0,1,0,0,1,
1,1,0,0,0,0,0,0,0,1,0,1,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0,
1,1,0,1,0,1,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1,1,1,1,0,1,0,1,0,0,1,
1,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0,0,1,0,1,0,1,0,0,0,1,1,0,1,0,1,0,1,1,0,1,1,1,0,0,0,0,1,1,0,1,0,1,
1,1,1,0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,1,0,
1,0,0,0,0,1,0,0,0,1,1,0,0,0,0,1,1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,
1,1,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,0,1,1,0,1,0,1,1,0,1,0,1,0,1,0,0,0,0,1,
1,0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,1,0,1,0,1,
1,1,0,1,0,0,0,0,1,0,0,0,1,1,0,0,1,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,1,1,1,1,0,1,0,0,1,0,
1,0,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0,
1,1,1,0,1,0,0,0,0,0,0,1,0,0,1,1,1,0,1,1,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,1,0,1,1,0,1,1,1,0,1,0,0,0,
1,0,0,0,0,0,1,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,1,1,0,1,0,0,0,0,0,0,1,1,0,0,1,1,
1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1,1,1,1,1,0,0,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,
1,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,0,0,0,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,1,0,1,1,1,0,1,0,0,0,
1,0,0,1,1,1,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1,1,
1,1,0,0,0,0,0,0,1,1,0,0,1,1,1,0,1,0,1,1,1,0,1,0,0,0,1,0,0,0,1,1,0,1,1,1,0,1,0,1,0,1,1,0,1,1,1,1,0,0,0,
};
int dirx[4]={1,0,0,-1};
int diry[4]={0,-1,1,0};
const char dir[5]={'D','L','R','U'} ;
char a[row*col+5];
string ans;
bool cheak(int x,int y)
{//判断这个点是否越界,是否可以走
return x>0 && x<row+1 && y>0 && y<col+1 && !maze[x][y];
}
void dfs(int x,int y,int pos)
{
if(pos>best)//如果当前路径已经走的步长pos大于之前最短补偿best
return;//就不需要沿着现有路径继续走下去了,这个剪枝可以加快速度
if(x==row && y==col)
{//已经到达终点
string temp;
for(int i=0;i<pos;i++)
temp+=a[i];
if(pos<best)//将更短的路径记录下来
{
ans=temp;
best=pos;
}
else if(pos==best && temp<ans)
ans=temp;
return;
}
for(int i=0;i<4;i++)
{//四个方向
int tox=x+dirx[i];
int toy=y+diry[i];//走向(tox,toy) 位置
if(cheak(tox,toy) && pos+1<=mins[tox][toy])
{//(tox,toy)符合cheak且当前走法能够使到达 (tox,toy)的步数更小,就进入if内
maze[tox][toy]=1;//已经走过的路就标记一下
mins[tox][toy]=pos+1;//当前的走法到达tox,toy的步数比以前少,就把当前走法的步数更新
a[pos]=dir[i];//记录第pos步的方位
dfs(tox,toy,pos+1);//继续以(tox,toy,pos+1)深搜
maze[tox][toy]=0;//恢复(tox,toy)为0,即可行状态,以便其他走法尝试在这个位置探索
}
}
}
int main()
{
memset(mins,1,sizeof(mins));
best=99999999;
maze[1][1]=1;//标记起点走过了,为障碍物
dfs(1,1,0);
cout<<ans<<endl;
cout<<best<<endl;
return 0;
}
接下来用BFS求解我们就只需要处理字典序的问题即可,完整代码如下:
#include <iostream>
#include <queue>
using namespace std;
#define maxn 50
const int row=30;
const int col=50;
int step=0;
string maze[30]={
"01010101001011001001010110010110100100001000101010",
"00001000100000101010010000100000001001100110100101",
"01111011010010001000001101001011100011000000010000",
"01000000001010100011010000101000001010101011001011",
"00011111000000101000010010100010100000101100000000",
"11001000110101000010101100011010011010101011110111",
"00011011010101001001001010000001000101001110000000",
"10100000101000100110101010111110011000010000111010",
"00111000001010100001100010000001000101001100001001",
"11000110100001110010001001010101010101010001101000",
"00010000100100000101001010101110100010101010000101",
"11100100101001001000010000010101010100100100010100",
"00000010000000101011001111010001100000101010100011",
"10101010011100001000011000010110011110110100001000",
"10101010100001101010100101000010100000111011101001",
"10000000101100010000101100101101001011100000000100",
"10101001000000010100100001000100000100011110101001",
"00101001010101101001010100011010101101110000110101",
"11001010000100001100000010100101000001000111000010",
"00001000110000110101101000000100101001001000011101",
"10100101000101000000001110110010110101101010100001",
"00101000010000110101010000100010001001000100010101",
"10100001000110010001000010101001010101011111010010",
"00000100101000000110010100101001000001000000000010",
"11010000001001110111001001000011101001011011101000",
"00000110100010001000100000001000011101000000110011",
"10101000101000100010001111100010101001010000001000",
"10000010100101001010110000000100101010001011101000",
"00111100001000010000000110111000000001000000001011",
"10000001100111010111010001000110111010101101111000"};
bool vis[maxn][maxn];//标记
const int dirx[4]={1,0,0,-1};
const int diry[4]={0,-1,1,0};
const char dir[5]={'D','L','R','U'};
bool cheak(int x,int y)
{
return x>=0 && x<30 && y>=0 && y<50 && maze[x][y]=='0';
}
struct node
{
int x,y,step;//某个位置的x,y坐标值
//按照某种路径从起点到走到此处的步数为step
char direction;//存储D L R U,怎么走到这个位置的
};
node father[maxn][maxn];//当前结点的父节点
node now,nextpos;//指向当前和下一个位置
void dfs(int x,int y)
{//递归打印
if(x==0&&y==0)//找到起点开始正向打印路径
return;//直到搜到(0,0)位置而终止
else
dfs(father[x][y].x,father[x][y].y) ;//father[x][y]存储了他上一个位置在哪,那么就可以顺藤摸瓜
cout<<father[x][y].direction;//打印出所记录的2=direction方位
}
void bfs(int x,int y)
{
queue<node> q;
now.x=x;
now.y=y;
now.step=0;
q.push(now);
father[x][y].x=10000;
father[x][y].y=10000;
father[x][y].direction=0;
vis[x][y]=true;
while(!q.empty())
{//队列为空就不做了,能达到的位置全都宽搜达到
now=q.front() ;//获得队首元素,作为当前位置
q.pop();//队首元素出队列
for (int i=0;i<4;i++)
{
int tox=now.x+dirx[i];
int toy=now.y+diry[i];
if(cheak(tox,toy) && !vis[tox][toy])
{
vis[tox][toy]=true;
nextpos.x=tox;
nextpos.y=toy;
nextpos.step=now.step+1;
q.push(nextpos);
father[tox][toy].x=now.x;
father[tox][toy].y=now.y;
father[tox][toy].direction=dir[i];
}
}
}
}
int main()
{
bfs(0,0);
dfs(29,49);
return 0;
} 在使用BFS时我们使用queue容器是一个很好的工具,强烈安利!
以上两种方法都可以实现最优解,那么有什么区别呢?我们又该如何选择呢?
其实我们很容易选择,DFS的时间复杂度为O(V^2),而BFS的时间复杂度为O(V),再看如下两张图片:


我们可以很明显的看到DFS用时25ms,而BFS只用时4ms,相同的结果,DFS耗时是BFS的5倍还多!所以该用哪种方法求最优解也就不用多说了!
1.1.2陷阱版
能解决上述简单问题后,我们下面尝试用BFS解决迷宫加入陷阱后的问题:
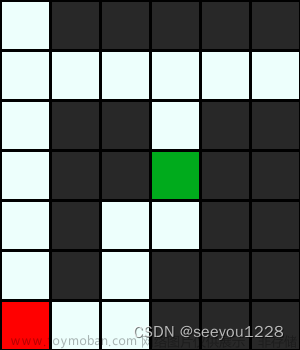
问题描述:迷宫的起始位置在左上角,终点位置在右下角。每一步,可以移动到上下左右相邻的格子中(前提是目标格子可以经过)。迷宫中有些格子可以经过,我们用 '.' 表示。有些格子是墙壁,不能经过,我们用 '#' 表示。此外,有些格子上有陷阱,我们用 'X' 表示。除非我们处于无敌状态,否则不能经过。有些格子上有无敌道具,我们用 '%' 表示。当我们第一次到达该格子时,自动获得无敌状态,无敌状态会持续 K 步。之后如果再次到达该格子不会获得无敌状态了。处于无敌状态时,可以经过有陷阱的格子,但是不会拆除/毁坏陷阱,即陷阱仍会阻止没有无敌状态的我们经过。给定迷宫(有我们自己输入迷宫和无敌步数K),请你最少经过几步可以离开迷宫?
仔细看题我们不难发现其实这个和上一个只是有无陷阱的区别,所以大致是一样的,那么在解题时只是如下while循环内部有差别:
while(!q.empty())
{
node now=q.front();
q.pop();
if(now.x==n-1 && now.y==n-1)//到达终点
return now.step;
//遍历上下左右四个点
for(int i=0;i<4;i++)
{
int tox=now.x+dirx[i];
int toy=now.y+diry[i];
//越界或者为墙壁,不可达
if(!cheak(tox,toy))
continue;
//(tox,tpy)处有一个无敌道具,且此处未访问过
if(mp[tox][toy]=='%' && !vis[tox][toy][k])
{
vis[tox][toy][k]=true;
q.push(node(tox,toy,k,now.step+1));
}
else
{
//当前无敌,无论前方是陷阱还是道路都可以走
if(now.k && !vis[tox][toy][now.k-1])
{
vis[tox][toy][now.k-1]=true;
q.push(node(tox,toy,now.k-1,now.step+1));
}
//当前不无敌,而且前方为道路
else if(!now.k && mp[tox][toy]=='.' && !vis[tox][toy][0])
{
vis[tox][toy][0]=true;
q.push(node(tox,toy,0,now.step+1));
}
}
}
}和上一个问题相比,我们在讨论待探索的下一个节点时只需要额外加上三种情况:1、当前位置不无敌,但下一位置有无敌道具,且此前未访问过;2、当前位置无敌,无论前方是陷阱还是道路都可以走而且前方未访问;3、当前位置不无敌,而且前方是正常道路,且未访问。这样就把复杂的问题简单化了。完整代码如下:文章来源:https://www.toymoban.com/news/detail-639221.html
#include <iostream>
#include <queue>
using namespace std;
const int N = 1e3+10;
int n,k;
char mp[N][N];
bool vis[N][N][99];
int ans;
int dirx[5]={0,1,0,-1};
int diry[5]={1,0,-1,0};
struct node
{
int x,y,k,step;
node(int cx,int cy,int ck,int cs)
{
x=cx,y=cy,k=ck,step=cs;
}
};
bool cheak(int x,int y)
{
return x>=0 && x<n && y>=0 && y<n && mp[x][y]!='#';
}
int bfs()
{
queue<node> q;
//初始化(0,0)点
vis[0][0][0]=true;
q.push(node(0,0,0,0));
while(!q.empty())
{
node now=q.front();
q.pop();
if(now.x==n-1 && now.y==n-1)//到达终点
return now.step;
//遍历上下左右四个点
for(int i=0;i<4;i++)
{
int tox=now.x+dirx[i];
int toy=now.y+diry[i];
//越界或者为墙壁,不可达
if(!cheak(tox,toy))
continue;
//(tox,tpy)处有一个无敌道具,且此处未访问过
if(mp[tox][toy]=='%' && !vis[tox][toy][k])
{
vis[tox][toy][k]=true;
q.push(node(tox,toy,k,now.step+1));
}
else
{
//当前无敌,无论前方是陷阱还是道路都可以走
if(now.k && !vis[tox][toy][now.k-1])
{
vis[tox][toy][now.k-1]=true;
q.push(node(tox,toy,now.k-1,now.step+1));
}
//当前不无敌,而且前方为道路
else if(!now.k && mp[tox][toy]=='.' && !vis[tox][toy][0])
{
vis[tox][toy][0]=true;
q.push(node(tox,toy,0,now.step+1));
}
}
}
}
//可遍历的点遍历完了但是任然没有到达终点,表示不可到达,返回-1
return -1;
}
int main()
{
cin>>n>>k;
for(int i=0;i<n;i++)
cin>>mp[i];
ans=bfs();
cout<<ans<<endl;
return 0;
} 1.2其他问题应用
1.2.1七段码应用
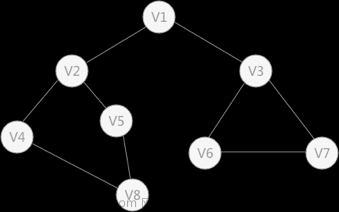
这个问题的关键一步就是通过判断将七个数字是否相连来创建邻接矩阵 ,这样就可以轻而易举地转换成搜索类问题去解决了。完整代码如下:
#include <iostream>
#include <cstring>
using namespace std;
int g[7][7]={
{0,1,0,0,0,1,0},
{1,0,1,0,0,0,1},
{0,1,0,1,0,0,1},
{0,0,1,0,1,0,0},
{0,0,0,1,0,1,1},
{1,0,0,0,1,0,1},
{0,1,1,0,1,1,0}
};
int bright[7];
int vis[7];
void dfs(int stick)
{
for(int i=0;i<7;i++)
{
if(g[stick][i] && bright[i] && !vis[i])
{
vis[i]=1;
dfs(i);
}
}
return;
}
int main()
{
int i,j,stick,x,ans=127;
for(i=1;i<=127;i++)
{
memset(bright,0,sizeof(bright));
memset(vis,0,sizeof(vis));
x=i,j=0;
while(x)
{
if(x%2)
bright[j]=1;
x/=2;
j++;
}
stick=0;
while(!bright[stick])
stick++;
vis[stick]=1;
dfs(stick);//vis
for(int k=0;k<7;k++)
{
if(bright[k] && !vis[k])
{
ans--;
break;
}
}
}
cout<<ans<<endl;
return 0;
} 以上就是我最近学习BFS和DFS解决搜索类问题的心得了,文章如果有不正确的内容还请各位批评指正!文章来源地址https://www.toymoban.com/news/detail-639221.html
到了这里,关于深度优先搜索(DFS)和广度优先搜索(BFS)两种算法c++的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!