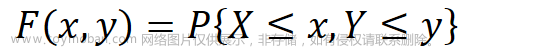多维随机变量及分布
X
X
X为随机变量,
∀
x
∈
R
,
P
{
X
≤
x
}
=
F
(
x
)
\forall x\in R,P\{X\le x\}=F(x)
∀x∈R,P{X≤x}=F(x)
设
F
(
x
)
F(x)
F(x)为
X
X
X的分布函数,则
(1)
0
≤
F
(
x
)
≤
1
0\le F(x)\le1
0≤F(x)≤1
(2)
F
(
x
)
F(x)
F(x)不减
(3)
F
(
x
)
F(x)
F(x)右连续
(4)
F
(
−
∞
)
=
0
,
F
(
+
∞
)
=
1
F(-\infin)=0,F(+\infin)=1
F(−∞)=0,F(+∞)=1
二维随机变量及分布
1.基本概念
二维随机变量,
E
E
E为随机实验,
Ω
\Omega
Ω为样本空间,若
∀
ω
∈
Ω
\forall\omega\in\Omega
∀ω∈Ω,
∃
\exists
∃唯一一对实数
(
X
,
Y
)
(X,Y)
(X,Y)与
ω
\omega
ω对应,称
(
X
,
Y
)
(X,Y)
(X,Y)为二维随机变量
2.分布函数
(1)
∀
x
,
y
∈
R
,
P
{
X
≤
x
,
Y
≤
y
}
=
F
(
x
,
y
)
\forall x,y\in R,P\{X\le x,Y\le y\}=F(x,y)
∀x,y∈R,P{X≤x,Y≤y}=F(x,y)
(2)
(
X
,
Y
)
(X,Y)
(X,Y)为二维随机变量
P
{
X
≤
x
}
=
F
X
(
x
)
P\{X\le x\}=F_X(x)
P{X≤x}=FX(x),
X
X
X的边缘分布函数
P
{
Y
≤
y
}
=
F
Y
(
y
)
P\{Y\le y\}=F_Y(y)
P{Y≤y}=FY(y),
Y
Y
Y的边缘分布函数
(3)
(
X
,
Y
)
(X,Y)
(X,Y)为二维随机变量
设
F
(
x
,
y
)
F(x,y)
F(x,y)为二维随机变量
(
X
,
Y
)
(X,Y)
(X,Y)的联合分布函数,则
(1)
0
≤
F
(
x
,
y
)
≤
1
0\le F(x,y)\le1
0≤F(x,y)≤1
(2)
F
(
x
,
y
)
F(x,y)
F(x,y)关于
x
,
y
x,y
x,y不减
(3)
F
(
x
)
F(x)
F(x)关于
x
,
y
x,y
x,y右连续
(4)
F
(
−
∞
,
−
∞
)
=
0
,
F
(
−
∞
,
+
∞
)
=
0
,
F
(
+
∞
,
−
∞
)
=
0
F(-\infin,-\infin)=0,F(-\infin,+\infin)=0,F(+\infin,-\infin)=0
F(−∞,−∞)=0,F(−∞,+∞)=0,F(+∞,−∞)=0
F
(
+
∞
,
+
∞
)
=
1
F(+\infin,+\infin)=1
F(+∞,+∞)=1
二维离散型变量及分布
1.二维离散型变量
(
X
,
Y
)
(X,Y)
(X,Y)为二维随机变量,若
(
X
,
Y
)
(X,Y)
(X,Y)可能取值为有限个或可列个,称
(
X
,
Y
)
(X,Y)
(X,Y)为二维离散型变量
2.二维离散型变量联合分布律与边缘分布律
(
X
,
Y
)
(X,Y)
(X,Y)为二维联合分布函数为
P
{
X
≤
x
,
Y
≤
y
}
=
F
(
x
,
y
)
P\{X\le x,Y\le y\}=F(x,y)
P{X≤x,Y≤y}=F(x,y)
若
∃
f
(
x
,
y
)
≥
0
\exists f(x,y)\ge 0
∃f(x,y)≥0使得
∫
−
∞
x
d
x
∫
−
∞
y
f
(
x
,
y
)
d
y
=
F
(
x
,
y
)
\int_{-\infin}^{x}dx\int_{-\infin}^yf(x,y)dy=F(x,y)
∫−∞xdx∫−∞yf(x,y)dy=F(x,y)
称
(
X
,
Y
)
(X,Y)
(X,Y)为二维连续型变量,
f
(
x
,
y
)
f(x,y)
f(x,y)称为
(
X
,
Y
)
(X,Y)
(X,Y)的联合密度函数(
f
(
x
,
y
)
≥
0
且
∫
−
∞
∞
d
x
∫
−
∞
∞
f
(
x
,
y
)
d
y
=
1
f(x,y)\ge0且\int_{-\infin}^{\infin}dx\int_{-\infin}^{\infin}f(x,y)dy=1
f(x,y)≥0且∫−∞∞dx∫−∞∞f(x,y)dy=1)
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
=
f
X
(
x
)
\int_{-\infin}^{+\infin}f(x,y)dy=f_X(x)
∫−∞+∞f(x,y)dy=fX(x),
X
X
X的边缘密度函数
∫
−
∞
+
∞
f
(
x
,
y
)
d
x
=
f
Y
(
y
)
\int_{-\infin}^{+\infin}f(x,y)dx=f_Y(y)
∫−∞+∞f(x,y)dx=fY(y),
Y
Y
Y的边缘密度函数
二维连续型变量均匀分布
定义
D
D
D为
x
o
y
xoy
xoy面内有限区域,其面积为
A
A
A。若二维连续型随机变量
(
X
,
Y
)
(X,Y)
(X,Y)的联合密度为
f
(
x
,
y
)
=
{
1
A
,
(
x
,
y
)
∈
D
0
,
(
x
,
y
)
∉
D
f(x,y)=\left\{ \begin{array}{l} \frac 1 A,(x,y)\in D \\0,(x,y)\notin D \end{array} \right.
f(x,y)={A1,(x,y)∈D0,(x,y)∈/D
称
(
X
,
Y
)
(X,Y)
(X,Y)在
D
D
D上服从均匀分布,记
(
X
,
Y
)
∼
U
(
D
)
(X,Y)\sim U(D)
(X,Y)∼U(D)文章来源:https://www.toymoban.com/news/detail-639622.html
二维正太分布
设
(
X
,
Y
)
(X,Y)
(X,Y)为二维连续型随机变量,若
(
X
,
Y
)
(X,Y)
(X,Y)的联合密度函数为
f
(
x
,
y
)
=
1
2
π
σ
1
σ
2
1
−
ρ
2
e
1
−
2
(
1
−
ρ
2
)
[
(
x
−
μ
1
)
2
σ
1
2
−
2
ρ
x
−
μ
1
σ
1
y
−
μ
2
σ
2
+
(
y
−
μ
2
)
2
σ
2
2
]
f(x,y)=\frac 1 {2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{\frac 1 {-2(1-\rho^2)}[\frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{x-\mu_1}{\sigma_1}\frac{y-\mu_2}{\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}]}
f(x,y)=2πσ1σ21−ρ21e−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1x−μ1σ2y−μ2+σ22(y−μ2)2]
称
(
X
,
Y
)
(X,Y)
(X,Y)服从以
μ
1
,
μ
2
,
σ
1
2
,
σ
2
2
,
ρ
\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho
μ1,μ2,σ12,σ22,ρ为参数的二维正太分布,记
(
X
,
Y
)
∼
N
(
μ
1
,
μ
2
,
σ
1
2
,
σ
2
2
,
ρ
)
(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)
(X,Y)∼N(μ1,μ2,σ12,σ22,ρ)文章来源地址https://www.toymoban.com/news/detail-639622.html
到了这里,关于概率论:多维随机变量及分布的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!