常见的数据结构：树Tree-Toy模板网

这篇具有很好参考价值的文章主要介绍了常见的数据结构：树Tree。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.概念

1.1 满二叉树

1.2 完全二叉树

1.3 平衡二叉树

2.遍历方式

2.1 先序遍历

2.2 中序遍历

2.3 后序遍历

2.4 层序遍历

1.概念

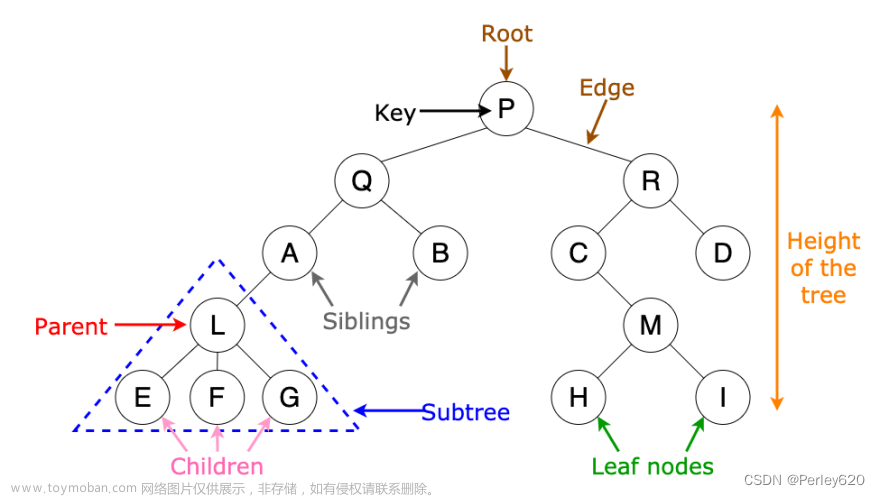
原理：一种特殊的数据结构，每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树

二叉树的分类：满二叉树、完全二叉树、平衡二叉树

存储方式：数组或者链表实现

遍历方式：先序遍历、中序遍历、后序遍历、层序遍历

1.1 满二叉树

二叉树的每一层节点树都达到最大值，就叫做满二叉树

数学表示：层数为 K，结点总数就为(2^k) -1 常见的数据结构：树Tree,数据结构

1.2 完全二叉树

二叉树除了最后一层外，其余层都是满二叉树，且最后一层是满的或者是右边缺少若干节点

常见的数据结构：树Tree,数据结构

1.3 平衡二叉树

树的左右子树的高度差绝对值不超过1，且左右子树也为平衡二叉树

常见的数据结构：树Tree,数据结构

2.遍历方式

2.1 先序遍历

先输出根节点，然后遍历左子树，最后遍历右子树

代码示例：

public void preOrder(TreeNode root){
	if(root == null){
		return;
	}
	system.out.println(root.data);
	preOrder(root.left);
	preOrder(root.right);
}

2.2 中序遍历

先遍历左子树，然后遍历根节点，最后遍历右子树

public void inOrder(TreeNode root){
	if(root == null){
		return;
	}
	inOrder(root.left);
	system.out.println(root.data);
	inOrder(root.right);
}

2.3 后序遍历

先遍历左子树，然后遍历右子树，最后遍历根节点

public void postOrder(TreeNode root){
	if(root == null){
		return;
	}
	postOrder(root.left);
	postOrder(root.right);
	system.out.println(root.data);
}

2.4 层序遍历

按照层级遍历，逐层从左到右访问所有节点文章来源地址https://www.toymoban.com/news/detail-639974.html

public List<List<Integer>> levelOrder(TreeNode root){
    //用一个二维数组存储最终层序遍历出的元素
    List<List<Integer>> result = new ArrayList<>();
    if(null == root){
        return result;
    }
    
    //创建一个队列用来存入树节点
    Queue queue = new LinkedList();
    queue.add(root);

    while(!queue.isEmpty){
        int len = queue.size();
        List<Integer> list= new ArrayList();
        while(len > 0){
            TreeNode temp = queue.poll();
            list.add(temp.val);
            
            //如果节点左右有值就加入队列
            if(temp.left != null){
                queue.add(temp.left);
            }
            if(temp.right!= null){
                queue.add(temp.right);
            }
            len --;
        }
        result.add(list);
    }
    return result;
}

到了这里，关于常见的数据结构：树Tree的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！