CNN卷积神经网络之反向传播过程

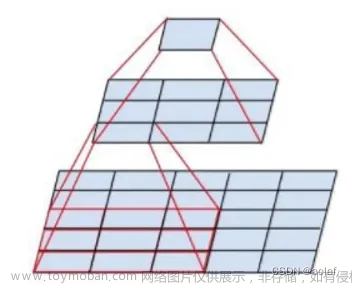
1. 正向传播过程

1.1 卷积层-卷积运算

我们假设卷积运算如下(其中couv代表卷积运算，w是卷集核的数据，卷积核为2*2，b为偏置数)。建设上一层输出的特征图是$3\ast 3$,经过卷积运算以及加上偏置结果如下：
[ a 11 l − 1 a 12 l − 1 a 13 l − 1 a 21 l − 1 a 22 l − 1 a 23 l − 1 a 31 l − 1 a 32 l − 1 a 33 l − 1 ] c o u v [ w 11 l w 12 l w 21 l w 22 l ] + [ b 11 l b 12 l b 21 l b 22 l ] = [ z 11 l z 12 l z 21 l z 22 l ] (1) \begin{bmatrix} a_{11}^{l-1} & a_{12}^{l-1} & a_{13}^{l-1} \\ a_{21}^{l-1} & a_{22}^{l-1} & a_{23}^{l-1} \\ a_{31}^{l-1} & a_{32}^{l-1} & a_{33}^{l-1} \\ \end{bmatrix} couv \begin{bmatrix} w_{11}^{l}& w_{12}^{l}\\ w_{21}^{l}& w_{22}^{l}\\ \end{bmatrix} + \begin{bmatrix} b_{11}^{l}& b_{12}^{l}\\ b_{21}^{l}& b_{22}^{l}\\ \end{bmatrix} =\begin{bmatrix} z_{11}^{l}& z_{12}^{l}\\ z_{21}^{l}& z_{22}^{l}\\ \end{bmatrix} \tag{1} ​a11l−1​a21l−1​a31l−1​​a12l−1​a22l−1​a32l−1​​a13l−1​a23l−1​a33l−1​​ ​couv[w11l​w21l​​w12l​w22l​​]+[b11l​b21l​​b12l​b22l​​]=[z11l​z21l​​z12l​z22l​​](1)

其中$\hat{y}$代表预测值(对输出的值经过激活函数的结果)：
$$\hat{y}=\sigma (z^l)\text{\hspace{1em}(2)}$$

1.2 池化层-向下采样

池化有平均池化和最大池化，这里以平均池化为例子。即将原始矩阵按照指定的大小比例进行缩放。将原始矩阵缩小到一个更小的尺寸，通过将相邻元素的值进行平均来得到新的缩放后的矩阵
m a t r i x = [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ] matrix = \left[\begin {array}{c} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \\ \end{array}\right] matrix= ​15913​261014​371115​481216​ ​
设置池化层大小为$2\ast 2$，则$4\ast 4$的矩阵经过池化层后输出的矩阵大小为$2\ast 2$

• 对于第一行第一列的元素：计算原始矩阵中小区域 {(0, 0), (0, 1), (1, 0), (1, 1)} 内元素的平均值：(1 + 2 + 5 + 6) / 4 = 3.5，将其赋值给 scaledMatrix[0][0]。
• 最终的矩阵
  $$\left[\begin{array}{cc}3.5& 5.5\\ 11.5& 13.5\end{array}\right]$$

2. 输出层误差项

输出层的误差项通过损失函数相对于输出的梯度来计算

2.1 损失函数

• 均方误差(MSE)，适用于回归问题
  $$MSE=\frac{1}{n}\sum _{i=1}^n(\widehat{y_i}-y_i{)}^2$$
  $y_i$是真实的值；$\widehat{y_i}$是预测值
• 交叉熵损失 适用于分类问题
  $$Cross-entropyloss=-\sum _{i=1}^n{y}_i\log (\widehat{y_i})$$

2.2 误差项推导过程

为了方便计算，我们选择的损失函数为MSE,n去2；$y_i$是真实的值；$\widehat{y_i}$是预测值，则损失函数$J$则表示为：
$$J=\frac{1}{2}(\widehat{y_i}-y_i{)}^2\text{\hspace{1em}(3)}$$
我们由(2)知道$\widehat{y_i}$的表达式，所以 计算损失函数对于输出层的加权输入$z^l$的偏导数(这里采用了链式法则)
$$\frac{\partial J}{\partial z^l}=\frac{\partial J}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial z^l}\text{\hspace{1em}(4)}$$
而在这个公式中$\frac{\partial J}{\partial \hat{y}}$可以计算出，我们$J$是用的均方误差函数
$$\frac{\partial J}{\partial \hat{y}}=\hat{y}-y\text{\hspace{1em}(5)}$$
所以输出层的误差项通过损失函数相对于输出的梯度
$${\delta }^l=\frac{\partial J}{\partial z^l}=（\hat{y}-y)\cdot {\sigma }^{\prime }(z^l)\text{\hspace{1em}(6)}$$

假设这里用的激活函数是sigmod函数。
$$\frac{\partial \hat{y}}{\partial z^l}={\sigma }^{\prime }(z^l)=\sigma (z^l)\cdot (1-\sigma (z^l))\text{\hspace{1em}(7)}$$

$$\frac{\partial J}{\partial z^l}=(\hat{y}-y)\cdot {\sigma }^{\prime }(z^l)=(\hat{y}-y)\cdot \sigma (z^l)\cdot (1-\sigma (z^l))\text{\hspace{1em}(8)}$$

3. 已知卷积层的误差，推上一层(反卷积)

3.1 池化层的误差项

假设我们的卷积层为${\delta }^l$，推上一层池化层${\delta }^{l-1}$，我们要结合卷积层误差项${\delta }^l$去推上一层的误差项。

3.1.1 推导过程

在卷积层中，我们卷积计算后还需要进行激活函数处理。例如公式(2)表达式,我们进一步细化这个公式：
$$\hat{y}=a^l=\sigma (z^L)=\sigma (a^{l-1}\ast W^l+b^l)\text{\hspace{1em}(9)}$$
$$\frac{\partial \hat{y}}{\partial z^l}=\frac{\partial a^l}{\partial z^l}={\sigma }^{\prime }(z^L)\text{\hspace{1em}(10)}$$
那${\delta }^{l-1}$的误差项:
$$\begin{array}{c}\begin{array}{rl}{\delta }^{l-1}& =\frac{\partial J}{\partial z^{l-1}}\text{(链式法则去化解)}\\ & =\frac{\partial J}{\partial z^l}\cdot \frac{\partial z^l}{\partial z^{l-1}}\\ & ={\delta }^l\cdot \frac{\partial z^l}{\partial a^{l-1}}\cdot \frac{\partial a^{l-1}}{\partial z^{l-1}}\\ & ={\delta }^l\cdot \frac{\partial z^l}{\partial a^{l-1}}\cdot {\sigma }^{\prime }(z^{l-1})\end{array}\end{array}\text{\hspace{1em}(11)}$$
这是我们来单独看这里面的一些符号：

• $\frac{\partial z^l}{\partial a^{l-1}}$
  我们知道如下公式不难得出：(可以参考卷积层卷积运算公式)
  $$z^l=w^l\cdot a^{l-1}+b^l\text{\hspace{1em}(12)}$$
  那对公式12求导则
  $$\frac{\partial z^l}{\partial a^{l-1}}=w^l\text{\hspace{1em}(13)}$$
• ${\delta }^l\cdot \frac{\partial z^l}{\partial a^{l-1}}$他们之间有啥关联吗？
  $$\begin{array}{c}\begin{array}{rl}\nabla a& ={\delta }^l\cdot \frac{\partial z^l}{\partial a^{l-1}}\text{(链式法则)}\\ & ={\delta }^l\cdot w^l\\ & =\frac{\partial J}{\partial z^l}\cdot \frac{\partial z^l}{\partial a^{l-1}}\\ & =\frac{\partial J}{\partial a^{l-1}}\end{array}\end{array}\text{\hspace{1em}(14)}$$
  从这个公式知道$\nabla a$代表损失函数$J$关于$a^{l-1}$的导数,即我们每个矩阵值的误差项。我们根据损失函数的变化情况来更新网络的参数，从而优化网络的性能。梯度下降算法。
• 结合$\nabla a$来尝试计算卷积层的误差项，会有什么规律。
  我们根据文章上面卷积层-卷积运算的例子来细化每一个z的取值
  $$\begin{gathered} z_{11}=a_{11}\cdot w_{11}+a_{12}\cdot w_{12}+a_{21}\cdot w_{21}+a_{22}\cdot w_{22}+b_{11} \\ {z}_{12}=a_{12}\cdot w_{11}+a_{13}\cdot w_{12}+a_{22}\cdot w_{21}+a_{23}\cdot w_{22}+b_{12} \\ {z}_{21}=a_{21}\cdot w_{11}+a_{22}\cdot w_{12}+a_{31}\cdot w_{21}+a_{32}\cdot w_{22}+b_{21} \\ {z}_{22}=a_{22}\cdot w_{11}+a_{23}\cdot w_{12}+a_{32}\cdot w_{21}+a_{33}\cdot w_{22}+b_{22}\text{\hspace{1em}(15)} \end{gathered}$$
  根据公式(15)得出$\nabla a$他们的每个的具体误差项
  $$\begin{array}{c}\begin{array}{rl}& \nabla a_{11}=\frac{\partial J}{\partial z_{11}}\cdot \frac{\partial z_{11}}{\partial a_{11}}={\delta }_{11}\cdot w_{11}\\ & \nabla a_{12}=\frac{\partial J}{\partial z_{12}}\cdot \frac{\partial z_{12}}{\partial a_{12}}+\frac{\partial J}{\partial z_{11}}\cdot \frac{\partial z_{11}}{\partial a_{12}}={\delta }_{12}\cdot w_{11}+{\delta }_{11}\cdot w_{12}\\ & \nabla a_{13}=\frac{\partial J}{\partial z_{12}}\cdot \frac{\partial z_{12}}{\partial a_{13}}={\delta }_{12}\cdot w_{12}\\ & \nabla a_{21}=\frac{\partial J}{\partial z_{11}}\cdot \frac{\partial z_{11}}{\partial a_{21}}+\frac{\partial J}{\partial z_{21}}\cdot \frac{\partial z_{21}}{\partial a_{21}}={\delta }_{11}\cdot w_{21}+{\delta }_{21}\cdot w_{11}\\ & \nabla a_{22}=\frac{\partial J}{\partial z_{11}}\cdot \frac{\partial z_{11}}{\partial a_{22}}+\frac{\partial J}{\partial z_{12}}\cdot \frac{\partial z_{12}}{\partial a_{22}}+\frac{\partial J}{\partial z_{21}}\cdot \frac{\partial z_{21}}{\partial a_{22}}+\frac{\partial J}{\partial z_{22}}\cdot \frac{\partial z_{22}}{\partial a_{22}}={\delta }_{11}\cdot w_{22}+{\delta }_{12}\cdot w_{21}+{\delta }_{21}\cdot w_{12}+{\delta }_{22}\cdot w_{11}\\ & \nabla a_{23}=\frac{\partial J}{\partial z_{12}}\cdot \frac{\partial z_{12}}{\partial a_{23}}+\frac{\partial J}{\partial z_{22}}\cdot \frac{\partial z_{22}}{\partial a_{23}}={\delta }_{12}\cdot w_{22}+{\delta }_{22}\cdot w_{12}\\ & \nabla a_{31}=\frac{\partial J}{\partial z_{21}}\cdot \frac{\partial z_{21}}{\partial a_{31}}={\delta }_{21}\cdot w_{21}\\ & \nabla a_{32}=\frac{\partial J}{\partial z_{21}}\cdot \frac{\partial z_{21}}{\partial a_{32}}+\frac{\partial J}{\partial z_{22}}\cdot \frac{\partial z_{22}}{\partial a_{32}}={\delta }_{21}\cdot w_{22}+{\delta }_{22}\cdot w_{21}\\ & \nabla a_{33}=\frac{\partial J}{\partial z_{22}}\cdot \frac{\partial z_{22}}{\partial a_{33}}={\delta }_{22}\cdot w_{22}\end{array}\end{array}$$
  把这个转换为卷积运算：
  [ ∇ a 11 ∇ a 12 ∇ a 13 ∇ a 21 ∇ a 22 ∇ a 23 ∇ a 31 ∇ a 32 ∇ a 33 ] = [ δ 11 ⋅ w 11 δ 12 ⋅ w 11 + δ 11 ⋅ w 12 δ 12 ⋅ w 12 δ 11 ⋅ w 21 + δ 21 ⋅ w 11 δ 11 ⋅ w 22 + δ 12 ⋅ w 21 + δ 21 ⋅ w 12 + δ 22 ⋅ w 11 δ 12 ⋅ w 22 + δ 22 ⋅ w 12 δ 21 ⋅ w 21 δ 21 ⋅ w 22 + δ 22 ⋅ w 21 δ 22 ⋅ w 22 ] \begin{bmatrix} \nabla a_{11} & \nabla a_{12} & \nabla a_{13} \\ \nabla a_{21} & \nabla a_{22} & \nabla a_{23} \\ \nabla a_{31} & \nabla a_{32} & \nabla a_{33} \\ \end{bmatrix}=\begin{bmatrix} \delta_{11}\cdot w_{11} & \delta_{12}\cdot w_{11} + \delta_{11}\cdot w_{12} & \delta_{12}\cdot w_{12} \\ \delta_{11}\cdot w_{21} + \delta_{21}\cdot w_{11} & \delta_{11} \cdot w_{22} + \delta_{12}\cdot w_{21} + \delta_{21}\cdot w_{12} + \delta_{22}\cdot w_{11} & \delta_{12}\cdot w_{22} + \delta_{22}\cdot w_{12} \\ \delta_{21}\cdot w_{21} & \delta_{21}\cdot w_{22} + \delta_{22}\cdot w_{21} & \delta_{22}\cdot w_{22} \\ \end{bmatrix} ​∇a11​∇a21​∇a31​​∇a12​∇a22​∇a32​​∇a13​∇a23​∇a33​​ ​= ​δ11​⋅w11​δ11​⋅w21​+δ21​⋅w11​δ21​⋅w21​​δ12​⋅w11​+δ11​⋅w12​δ11​⋅w22​+δ12​⋅w21​+δ21​⋅w12​+δ22​⋅w11​δ21​⋅w22​+δ22​⋅w21​​δ12​⋅w12​δ12​⋅w22​+δ22​⋅w12​δ22​⋅w22​​ ​

[ 0 0 0 0 0 δ 11 δ 12 0 0 δ 21 δ 22 0 0 0 0 0 ] c o n v [ w 22 w 21 w 12 w 11 ] = [ δ 11 ⋅ w 11 δ 12 ⋅ w 11 + δ 11 ⋅ w 12 δ 12 ⋅ w 12 δ 11 ⋅ w 21 + δ 21 ⋅ w 11 δ 11 ⋅ w 22 + δ 12 ⋅ w 21 + δ 21 ⋅ w 12 + δ 22 ⋅ w 11 δ 12 ⋅ w 22 + δ 22 ⋅ w 12 δ 21 ⋅ w 21 δ 21 ⋅ w 22 + δ 22 ⋅ w 21 δ 22 ⋅ w 22 ] \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & \delta_{11} & \delta_{12} & 0 \\ 0 & \delta_{21} & \delta_{22}& 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} conv \begin{bmatrix} w_{22}& w_{21}\\ w_{12}& w_{11}\\ \end{bmatrix}= \begin{bmatrix} \delta_{11}\cdot w_{11} & \delta_{12}\cdot w_{11} + \delta_{11}\cdot w_{12} & \delta_{12}\cdot w_{12} \\ \delta_{11}\cdot w_{21} + \delta_{21}\cdot w_{11} & \delta_{11} \cdot w_{22} + \delta_{12}\cdot w_{21} + \delta_{21}\cdot w_{12} + \delta_{22}\cdot w_{11} & \delta_{12}\cdot w_{22} + \delta_{22}\cdot w_{12} \\ \delta_{21}\cdot w_{21} & \delta_{21}\cdot w_{22} + \delta_{22}\cdot w_{21} & \delta_{22}\cdot w_{22} \\ \end{bmatrix} ​0000​0δ11​δ21​0​0δ12​δ22​0​0000​ ​conv[w22​w12​​w21​w11​​]= ​δ11​⋅w11​δ11​⋅w21​+δ21​⋅w11​δ21​⋅w21​​δ12​⋅w11​+δ11​⋅w12​δ11​⋅w22​+δ12​⋅w21​+δ21​⋅w12​+δ22​⋅w11​δ21​⋅w22​+δ22​⋅w21​​δ12​⋅w12​δ12​⋅w22​+δ22​⋅w12​δ22​⋅w22​​ ​

3.1.2 误差项表示

即卷积层的误差项是上一层池化层的误差项与卷积核大小旋转180度的卷积运算。即进一步蒋公式11化解：（其中池化层没有激活函数，或者可以理解$\delta (x)=x$ 求导就为1）
$${\delta }^{l-1}={\delta }^l\cdot \frac{\partial z^l}{\partial a^{l-1}}\cdot {\sigma }^{\prime }(z^{l-1})={\delta }^{l}conv(rot189(w^l))\cdot {\sigma }^{\prime }(z^{l-1})\text{\hspace{1em}(16)}$$

3.2 推导W和b的梯度

3.2.1 推导过程

我们知道这是对矩阵特征值的误差项，
$${\delta }^{l-1}=\frac{\partial J}{\partial z^{l-1}}$$
同理对$W$的梯度为：
$$\frac{\partial J}{\partial W^l}=\frac{\partial J}{\partial z^l}\cdot \frac{\partial z^l}{\partial W^l}={\delta }^l\frac{\partial z^l}{\partial W^l}\text{\hspace{1em}(17)}$$
同理计算机$\nabla a$，我们也可以计算出W的梯度：$\nabla W$ 如：
$$\nabla W_{11}=\frac{\partial J}{\partial z_{11}}\cdot \frac{\partial z_{11}}{\partial W_{11}}+\frac{\partial J}{\partial z_{12}}\cdot \frac{\partial z_{12}}{\partial W_{11}}+\frac{\partial J}{\partial z_{21}}\cdot \frac{\partial z_{21}}{\partial W_{11}}+\frac{\partial J}{\partial z_{22}}\cdot \frac{\partial z_{22}}{\partial W_{11}}={\delta }_{11}{a}_{11}+{\delta }_{12}{a}_{12}+{\delta }_{21}{a}_{21}+{\delta }_{22}{a}_{22}$$
同理$\nabla W_{12},\nabla W_{21},\nabla W_{22}$
[ ∇ W 11 ∇ W 12 ∇ W 21 ∇ W 22 ] = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] c o n v [ δ 11 δ 12 δ 21 δ 22 ] (18) \begin{bmatrix} \nabla W _{11} & \nabla W _{12} \\ \nabla W _{21} & \nabla W _{22} \\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} conv \begin{bmatrix} \delta _{11} & \delta _{12} \\ \delta _{21} & \delta _{22} \\ \end{bmatrix} \tag{18} [∇W11​∇W21​​∇W12​∇W22​​]= ​a11​a21​a31​​a12​a22​a32​​a13​a23​a33​​ ​conv[δ11​δ21​​δ12​δ22​​](18)

3.2.2 误差项表示

故权重的误差项为：
$$\frac{\partial J}{\partial W^l}=a^{l-1}conv({\delta }^l)\text{\hspace{1em}(19)}$$

3.2.3 偏执项b的误差

$$\frac{\partial J}{\partial b^l}=\sum _{uv}({\delta }^l{)}_{uv}\text{\hspace{1em}(20)}$$

4. 已知卷积层误差，推上一层误差(反池化)

在cnn中，池化层主要是缩放矩阵，在正向传播中，主要进行向下采样，在反向传播中，我们是倒着回去，应该向上采样来填充误差项。
在池化层，没有经过激活函数的，池化层主要有两种方法：最大池化层和平均池化层。假设我们把池化层误差项标记为：${\delta }^l$

4.1 平均池化层的误差项

假设池化层是将88的矩阵进行缩放，输出的特征图是44：
平均池化： [ 1 2 8 4 ] 反向传播 → [ 0.25 0.25 0.5 0.5 0.25 0.25 0.5 0.5 2 2 1 1 2 2 1 1 ] 平均池化：\begin{bmatrix} 1 & 2 \\ 8 & 4 \\ \end{bmatrix}\underrightarrow{反向传播} \begin{bmatrix} 0.25 & 0.25 & 0.5 & 0.5\\ 0.25 & 0.25 & 0.5 & 0.5 \\ 2 & 2 & 1 & 1 \\ 2 & 2 & 1 & 1 \\ \end{bmatrix} 平均池化：[18​24​] 反向传播​ ​0.250.2522​0.250.2522​0.50.511​0.50.511​ ​

4.2 最大池化层的误差项

最大池化在进行反向传播的时候，就需要把最大值放在之前做前向传播算法得到最大值的位置。（这里在进行卷积运算就要记录最大值的原始位置。）
最大池化： [ 1 2 8 4 ] 反向传播 → [ 1 0 0 0 0 0 2 0 0 8 0 0 0 0 4 0 ] 最大池化：\begin{bmatrix} 1 & 2 \\ 8 & 4 \\ \end{bmatrix}\underrightarrow{反向传播} \begin{bmatrix} 1& 0 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 8 & 0 & 0 \\ 0 & 0 & 4 & 0 \\ \end{bmatrix} 最大池化：[18​24​] 反向传播​ ​1000​0080​0204​0000​ ​文章来源地址https://www.toymoban.com/news/detail-640257.html

到了这里，关于CNN卷积神经网络之反向传播过程的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！