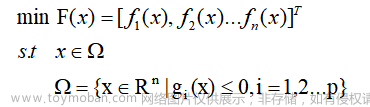NSGA-II算法实战（附MATLAB源码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了NSGA-II算法实战（附MATLAB源码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1、NSGA-II算法原理

NSGA-II算法全称非支配排序遗传算法II（Non-dominated Sorting Genetic Algorithm II， NSGA-II）。该算法是由 NSGA 改进而来的，用于解决复杂的、多目标优化问题。NSGA-II在NSGA的基础上引入了非支配排序、拥挤度、拥挤度比较算子和精英策略。下面将详细介绍非支配排序、拥挤度、拥挤度比较算子和精英策略三种方法。

(1) 非支配排序

非支配排序利用Pareto最优解的概念将种群中的个体进行分级，非支配状态越高的个体层级越靠前，从而能够挑选出个体中较为优异的，使其有较大机会进入下一迭代。

假设对于每个个体都有参数N(i)和S(i),其中N(i)表示种群中支配个体 i 的解个体的数量，S(i)可以支配个体 i 的解的集合。

其算法为：

（a）首先找到种群中N(i)=0的个体，将它存入到当前集合F1;

(b) 然后对于当前集合F1中的每个个体j,考察它所支配的个体集 S(j)，将集合 S(j) 中的每个个体 k 的 n(k) 减去1，即支配个体 k 的解个体数减1(因为支配个体 k 的个体 j 已经存入当前集 F1 )

(c) 如 n(k)-1=0则将个体 k 存入另一个集F2。最后，将 F1 作为第一级非支配个体集合，并赋予该集合内个体一个相同的非支配序 i(rank)，然后继续对 H 作上述分级操作并赋予相应的非支配序，直到所有的个体都被分级。重复步骤（a）-（b），直到所有个体处理完毕。

伪代码如下：

nsga-ii,数学建模,编程学习,算法,matlab,开发语言,Powered by 金山文档

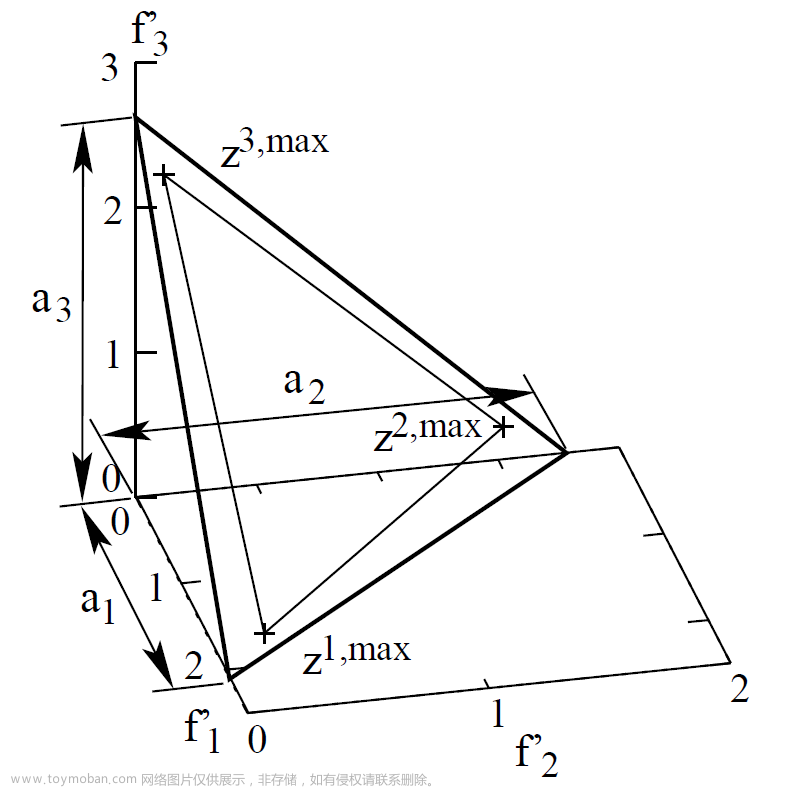
（2）拥挤度和拥挤度比较算子

拥挤度只适用于同一支配层级的个体之间的比较，通过对每个个体的每个目标函数进行计算拥挤度，进而得出每个个体的拥挤度，通过拥挤度比较个体的优异程度。拥挤度距离id定义如下：拥挤距离等于解在各个目标函数的方向上的前后两个解的距离和。在二维时，就等于图像矩形轴周长的一半。

其计算的伪代码如下：

拥挤度比较算子

从图中我们可以看出, 拥挤度距离id值较小时表示该个体周围比较拥挤。为了维持种群的多样性，我们需要一个比较拥挤度的算予以确保算法能够收敛到一个均匀分布的Pareto面上。在进行个体选择时，需要比较个体优劣，对于处于不同支配等级的个体，支配等级越低，则越优；对于处于同一支配等级的个体，则比较拥挤距离：距离越大，表明周围解的密度越小，则分布越均匀，则越优。其比较规则如下：

(3) 精英策略

为了防止当前群体的最优个体在下一代发生丢失，导致遗传算法不能收敛到全局最优解，精英策略被提出。把群体在进化过程中迄今出现最好的个体不进行遗传操作而直接复制到下一代中，一般会将其替换下一代中的最劣个体。精英保留策略改进了标准遗传算法的全局收敛能力。

(4)算法流程图

2、代码实战

%%主函数
%主程序
function Main()
clc;format short;addpath public;


    %算法名称
    Algorithm = {'NSGA-II'};
    %测试问题
    Problem = {'ZDT1'};
    %问题维数
    Objectives =2;


    %程序运行


    Start(Algorithm,Problem,Objectives,1);
end

%NSGA-II
function MAIN(Problem,M,Run)
clc;format compact;tic;
%-----------------------------------------------------------------------------------------
%参数设定
    [Generations,N] = P_settings('NSGA-II',Problem,M);
%-----------------------------------------------------------------------------------------
%算法开始
    %初始化种群
    [Population,Boundary,Coding] = P_objective('init',Problem,M,N);
     FunctionValue = P_objective('value',Problem,M,Population);
     FrontValue = DSort(FunctionValue);
     CrowdDistance = F_distance(FunctionValue,FrontValue);


    %开始迭代
    for Gene = 1 : Generations    
        %产生子代
        MatingPool = F_mating(Population,FrontValue,CrowdDistance);
        Offspring = P_generator(MatingPool,Boundary,Coding,N);
        Population = [Population;Offspring];
        FunctionValue = P_objective('value',Problem,M,Population);
        [FrontValue,MaxFront] = P_sort(FunctionValue,'half');
        CrowdDistance = F_distance(FunctionValue,FrontValue);


        %选出非支配的个体        
        Next = zeros(1,N);
        NoN = numel(FrontValue,FrontValue1:NoN) = find(FrontValue'descend');
        Next(NoN+1:N) = Last(Rank(1:N-NoN));


        %下一代种群
        Population = Population(Next,:);
        FrontValue = FrontValue(Next);
        CrowdDistance = CrowdDistance(Next);


        clc;fprintf('NSGA-II,第%2s轮,%5s问题,第%2s维,已完成%4s%%,耗时%5s秒\n',num2str(Run),Problem,num2str(M),num2str(roundn(Gene/Generations*100,-1)),num2str(roundn(toc,-2)));
    end
%-----------------------------------------------------------------------------------------     
%生成结果
    P_output(Population,toc,'NSGA-II',Problem,M,Run);
end

结果展示：文章来源地址https://www.toymoban.com/news/detail-640356.html