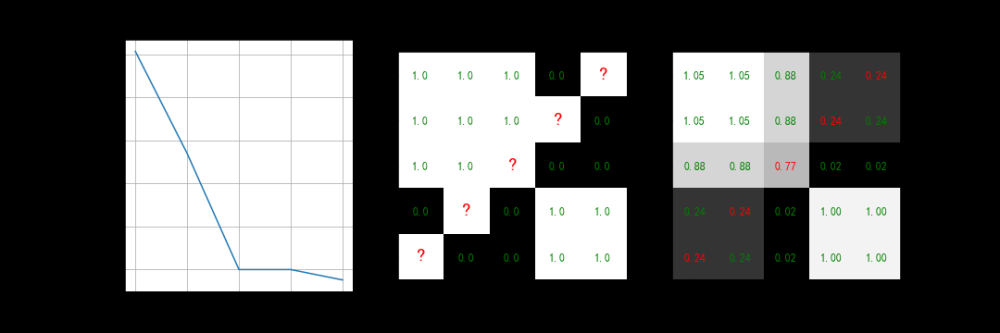
共现和上下文窗口
- 共现（
Co-occurrence）——对于给定的语料库，一对单词（如w1和w2）的共现是指它们在上、下文窗口中同时出现的次数。 - 上下文窗口（
Context Window）——指的是某个单词w的上下文范围的大小，也就是前后多少个单词以内的才算是上下文？一般，上、下文窗口由数字和方向指定。
示例中的上下文窗口为 2
共现矩阵的生成
-
由语料库中所有不重复单词构成矩阵A以存储单词的共现次数。
-
人为指定Context Window大小，计算每个单词在指定大小的上下文窗口中与它周围单词同时出现的次数。
-
依次计算语料库中各单词对的共现次数。
共现矩阵存在的问题及解决方法
- 共现矩阵增加了字典或词汇的大小（Increase in size with dictionary or vocabulary.）
- 对于一个庞大的语料库，这个共现矩阵可能变得非常复杂（高维），后续分类模型面临稀疏性问题，模型的健壮性较差。
奇异值分解（SVD）和主成分分析（PCA）是两种特征值方法，主要用于将高维数据集降维，同时保留重要信息。文章来源：https://www.toymoban.com/news/detail-641862.html
主成分分析 PCA
奇异值分解 SVD
文章来源地址https://www.toymoban.com/news/detail-641862.html
到了这里，关于Co-Occurrence Matrix——共现矩阵原理介绍的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
