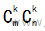GF256 = galois.GF(2**8)
A=GF256(matrix)
np.linalg.matrix_rank(A)
print('np.linalg.matrix_rank(A):',np.linalg.matrix_rank(A))
def is_all_sub_inverse(m, r, k):
subs = combinations(range(k), r)
num_subm=0
for idx in subs:
subm = m[:, idx]
GF4=galois.GF(2**2) # 4
subm=GF4(subm)
matrix_rank=np.linalg.matrix_rank(subm)
print('np.linalg.matrix_rank(subm):',matrix_rank)
if matrix_rank < 3:
print('False subm',subm)
return False
print('num_subm',num_subm)
return True
https://github.com/mhostetter/galois/issues
文章来源：https://www.toymoban.com/news/detail-642184.html
文章来源地址https://www.toymoban.com/news/detail-642184.html
到了这里，关于GF(2)上矩阵秩的快速计算的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
