【数据结构】二叉树常见题目

前言

此乃本人自用版本，用于复习回顾！ 所以部分题目不会有过大详细的解析，不懂的可以评论！笔者将竭力为你解答

二叉树概念

满二叉树

满⼆叉树：如果⼀棵⼆叉树只有度为0的结点和度为2的结点，并且度为0的结点在同⼀层上，则这棵⼆叉树为满⼆叉树

高度为h的满二叉树,共有2^h -1个节点

完全二叉树

完全⼆叉树的定义如下：在完全⼆叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最⼤值，并且最下⾯⼀层的节点都集中在该层最左边的若⼲位置。

完全二叉树的高度为h,则在第h层:包含 1~ 2^h -1个节点

完全二叉树的判断:

最后一层必须从左到右依次变满,如果不连续,就不符合完全二叉树

优先级队列其实是⼀个堆，堆就是⼀棵完全⼆叉树，同时保证⽗⼦节点的顺序关系

二叉搜索树(二叉排序树)

⼆叉搜索树是⼀个有序树

• 若它的左⼦树不空，则左⼦树上所有结点的值均⼩于它的根结点的值；
• 若它的右⼦树不空，则右⼦树上所有结点的值均⼤于它的根结点的值；
• 它的左、右⼦树也分别为⼆叉排序树

平衡⼆叉搜索树

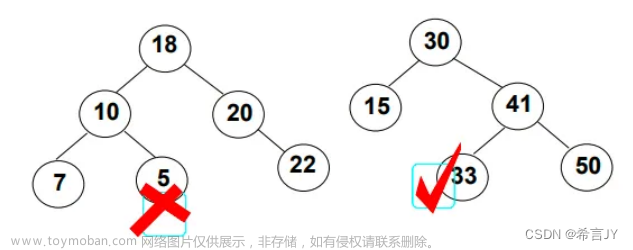
平衡⼆叉搜索树：⼜被称为AVL树

且具有以下性质：它是⼀棵空树或 它的左右两个⼦树的⾼度差的绝对值不超过1，并且左右两个⼦树都是⼀棵平衡⼆叉树

最后⼀棵树不是平衡⼆叉树，因为它的左右两个⼦树的⾼度差的绝对值超过了1

注意:C++中map、set、multimap，multiset的底层实现都是平衡⼆叉搜索树，所以map、set的增删操作
时间时间复杂度是log n 而：unordered_map底层实现是哈希表

存储⽅式

⼆叉树可以链式存储，也可以顺序存储

链式存储⽅式就⽤指针， 顺序存储的⽅式就是⽤数组

顺序存储:

其中我们也可以发现下标的规律:

• parent = (child-1)/2
• left_child = parent*2+1
• right_child = parent*2+2

链式存储:

我们通常使用的是链式存储

二叉树OJ

二叉树创建字符串

给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串,空节点使用一对空括号对 “()” 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对,

https://leetcode-cn.com/problems/construct-string-from-binary-tree/

前序遍历的方式, 先处理根节点:

左树怎么处理? 右树怎么处理? 什么时候需要加括号！

构建左树的括号的时候，如果左树存在 或者 左树不存在，右树存在，那么此时序列化这个左树需要加括号

//左树是否需要加括号:有左 || 无左有右  -> 就需要加括号
if(root->left || root->right)
{
   
    ans += '(';
    _tree2str(root->left,ans);
    ans += ')';
}

构建右树的括号的时候：如果右树存在就需要加

if(root->right)
{
   
    ans += '(';
    _tree2str(root->right,ans);
    ans += ')'; 
}

err:

方法1:

class Solution {
   
    public:
    string tree2str(TreeNode* root)
    {
   
        string ans;
        if(root == nullptr)
        {
   
            return ans;
        }
        ans += to_string(root->val);
        //有左 || 无左有右  -> 就需要加括号
        //root->left || root->right就可以代表上面的描述
        if(root->left || root->right)
        {
   
            ans += '(';
            ans += tree2str(root->left);
            ans += ')';
        }
        //右树只要不为空就加括号,否则不处理右树
        if(root->right)
        {
   
            ans += '(';
            ans += tree2str(root->right);
            ans += ')';
        }

        return ans;
    }
};

缺点: 每一次返回都是传值返回, 由于返回的ans是临时变量,不能使用引用返回, 所以是深拷贝

优化:写子函数,传引用作为参数,减少拷贝

class Solution {
   
    public:
    void _tree2str(TreeNode* root,string& ans)
    {
   
        if(root == nullptr)
        {
   
            return ;
        }
        //前序遍历序列化,需要判断是否需要加括号
        ans += to_string(root->val);
        //左树是否需要加括号:有左 || 无左有右  -> 就需要加括号
        if(root->left || root->right)
        {
   
            ans += '(';
            _tree2str(root->left,ans);
            ans += ')';
        }
        //判断右树是否需要加括号->右树不为空,就需要加
        if(root->right)
        {
   
            ans += '(';
            _tree2str(root->right,ans);
            ans += ')'; 
        }
    }
    string tree2str(TreeNode* root) {
   
        string ans;
        _tree2str(root,ans);
        return ans;
    }
};

二叉树的分层遍历1

https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

d

class Solution {
   
    public:
    vector<vector<int>> levelOrder(TreeNode* root) {
   
        vector<vector<int>> vv;
        if(root == nullptr)
        {
   
            return vv;//返回空容器
        }
        queue<TreeNode* >q;//用于层序遍历的容器
        q.push(root);//先把根节点入队列
        while(!q.empty())
        {
   
            int size = q.size();//这一层有多少个节点
            vector<int> v;
            for(int i =0;i<size;i++)
            {
   
                //对这一层的节点做处理
                TreeNode* node = q.front();
                q.pop();
                v.push_back(node->val);
                //左右孩子不为空,就进队列
                if(node->left)
                {
   
                    q.push(node->left);
                }
                if(node->right)
                {
   
                    q.push(node->right);
                }
            }
            //把这一层的结果放到容器中
            vv.push_back(v);
        }
        return vv;
    }
};

二叉树的分层遍历2

https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/

此题和上面的区别就是,这个是自底向上存放结果,而上一题是自顶向下存放结果,

所以我们处理的方法是：先得到自顶向下的结果,然后翻转容器,得到的就是自底向上的结果

class Solution {
   
public:
  vector<vector<int>> levelOrderBottom(TreeNode* root) {
   
        vector<vector<int>> vv;
        if(root == nullptr)
        {
   
            return vv;//返回空容器
        }
        queue<TreeNode* >q;//用于层序遍历的容器
        q.push(root);//先把根节点入队列
        while(!q.empty())
        {
   
            int size = q.size();//这一层有多少个节点
            vector<int> v;
            for(int i =0;i<size;i++)
            {
   
                //对这一层的节点做处理
                TreeNode* node = q.front();
                q.pop();
                v.push_back(node->val);
                //左右孩子不为空,就进队列
                if(node->left)
                {
   
                    q.push(node->left);
                }
                if(node->right)
                {
   
                    q.push(node->right);
                }
            }
            //把这一层的结果放到容器中
            vv.push_back(v);
        }
        reverse(vv.begin(),vv.end());
        return vv;
    }
};

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

什么叫公共祖先: 沿着自己的路径往上走,最坏就走到根节点, 二者的交点就是祖先

情况分析:该类题目的常见类型:

1.如果是三叉链

即左右孩子指针 + 父亲节点指针

此时可以转化为链表相交问题:

• 两个节点不断往上走到根节点位置,统计二者的长度,然后长链表先走差距步,然后二者再一起走,当二者相遇就是祖先

2.如果是搜索树:

a.如果一个值比当前root节点的值小,一个值比当前root节点的值大 ->我就是最近公共祖先

b.如果两个值都比当前root节点的值小 -> 去左树递归查找

c.如果两个值都比当前root节点的值大-> 去右树递归查找

3.普通的二叉树

相比搜索二叉树,此时不能使用值的大小去判断在左树还是右树！此时要整棵树查找

此时是第三种 普通二叉树的情况:

方法1:

设计一个子函数Find:用于查找x这个节点在不在

对要查找的两个节点的情况分析:

如果其中一个节点是当前根节点,最近公共祖先就是当前节点

如果两个节点不在root这棵树的同一侧:当前root节点就是二者的最近公共祖先

如果两个节点都在root的右树:去root的右树寻找

如果两个节点都在root的左数:去root的左树查找

为了方便,可以设计4个变量分别标志p和q是否在左树/右树

子函数Find:

//查找x这个节点是否在这棵树
bool Find(TreeNode* root,TreeNode* x)
{
   
    //root为空树
    if(root == nullptr) return false;

    //root就是x节点
    if(root == x) return true;

    //去左树和右树查找
    //任意一棵树找到就说明x在这棵树,所以用的是||的逻辑
    return Find(root->left,x) || Find(root->right,x);
}

主函数:

注意返回值的问题:

时间复杂度:O(N^2)

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
{
   
    //root为空树
    if(root == nullptr) return nullptr;

    //如果其中一个节点是当前根节点,最近公共祖先就是当前节点
    if(root == p || root == q)
    {
   
        return root;
    }
    //定义4个变量标志p和q在root的哪一侧
    bool pInLeft,pInRight,qInLeft,qInRight;
    //如果p/q在左树了就不可能在右树
    pInLeft = Find(root->left,p);//调用子函数查找p是否在root的左树
    pInRight = !pInLeft;
    
    qInLeft = Find(root->left,q);//调用子函数查找q是否在root的左树
    qInRight = !qInLeft;

    //对p和q的情况分析
    //1.两个节点不在同一侧:根节点就是祖先
    if((pInLeft&&qInRight) || (pInRight&&qInLeft))
    {
   
        return root;
    }
    //2.两个节点都在左树->去左树找
    else if(pInLeft&&qInLeft)
    {
   
        return lowestCommonAncestor(root->left,p,q);
    }
    //3.两个节点都在右树->去右树找
    else if(pInRight&&qInRight)
    {
   
        return lowestCommonAncestor(root->right,p,q);
    }
    else    //因为p和q都存在,所以不可能走到这里的else
    {
   
        //如果此处不返回,就会报错:不是所有路径都有返回值！
        //这是语法要求的
        return nullptr;
    }
}

方法2:分别求出从根节点到p和q的路径,再找两个路径的交点

这里可以选择把路径加入到栈中,注意栈中最好存放节点指针,如果存的是节点的值,如果存在树中存在相同的值,就会出错(虽然这题说了节点的值不重复)

FindPath函数:把从根节点到x的路径加入到容器中,

注意:要排除节点->回溯 时间复杂度:O(N)

子函数FindPath:查找x节点,并保存沿途的路径节点 返回值为bool类型,用于标志是否发现节点x

不管三七二十一,先把当前节点放到路径容器中

0.如果当前节点为空 ->返回false

1.如果当前节点就是x ->返回true
否则:
2.去左树查找,找到了就返回true,否则就是false
3.去右树查找,找到了就返回true,否则就是false
4.如果走到这一步,说明在当前节点的这颗子树不可能找到x节点,(说明该节点不是从根节点到x节点的路径中的一个节点) 把这个节点从就容器中去掉,然后返回false

• 上述第四步应该是返回false！！！手误

// 返回bool类型是为了判断是否发现x,发现了就不需要往下找了
//因为要修改path容器的内容,所以要传引用
bool FindPath(TreeNode* root,TreeNode* x,stack<TreeNode*>& path)
{
   
    //当前节点为空 ->返回false
    if(root == nullptr) return false;
    path.push(root);//先把当前节点放到路径中
    //当前节点就是x节点->返回true
    if(root == x) return true;
    //如果root不是x -> 去当前节点的左树和右树找x,并保存沿途的路径
    if(FindPath(root->left,x,path))
    {
   
        //在当前节点的左树中找到x了,返回true
        return true;
    }
    if(FindPath(root->right,x,path))
    {
   
        //在当前节点的右树找到x,返回true
        return true;
    }

    //走到这里,说明当前节点的左树和右树都没有找到x节点->把当前节点在路径中去掉,返回false
    path.pop();
    return false;
}

主函数:

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
{
   
    stack<TreeNode*> pPath,qPath;//分别保存到p和q的路径
    FindPath(root,p,pPath);//得到到p节点的路径,保存到pPath
    FindPath(root,q,qPath);//得到到q节点的路径,保存到qPath

    //长的路径容器先走差距步
    while(qPath.size() != pPath.size())
    {
   
        if(qPath.size() > pPath.size())
        {
   
            qPath.pop();
        }
        else
        {
   
            pPath.pop();
        }
    }
    //此时二者得路径长度相同,一起出数据
    //当二者栈顶元素相同,就是祖先
    while(qPath.top() != pPath.top())
    {
   
        qPath.pop();
        pPath.pop();
    }
    return qPath.top();
}

方法3：二叉树递归套路文章来源地址https://www.toymoban.com/news/detail-643046.html

class Solution {
   
public:
    struct Info
    {
   
        bool isFindQ;//是否发现q
        bool isFindP;//是否发现p
        TreeNode* ans;//记录q和p的公共祖先答案
        Info(bool isQ, bool isP,TreeNode* an)
        {
   
            isFindP = isP;
            isFindQ = isQ;
            ans = an;
        }
    };
    Info process(TreeNode* x,TreeNode* p,TreeNode* q)
    {
   
        if(x == nullptr)
        {
   
            return Info(false,false,nullptr);//设置空信息
        }
        Info leftInfo = process(x->left,p,q

到了这里，关于【数据结构】二叉树常见题目的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！