目录
1. 直线、线段和射线
1.1 直线
1.2 射线
2. 球
3. AABB
4. 平面
5. 三角形
6. 多边形
1. 直线、线段和射线
经典定义

书中对射线定义做了修改:有向线段。

1.1 直线
算法定义
Class line3D
{
public:
Vector3D origin; // 直线中的两个点表示该直线,其中这两个点用3d向量表示
Vector3D end;
//成员函数
}1.2 射线

p0是起始点,d是方向向量,单位向量。 自变量是t,可以很大超过1. p(0)=p0. p(2)=p0+2d;
算法实现
Class rayLine3D
{
public:
Vector3D rayOrigin; // p0, 射线起始点,用3d向量表示
Vector3D rayDelta; // d,一般是单位向量。
//成员函数
}2. 球

其中||p - c|| = r是球面公式,D=2r是直径,C是过球心切面的周长,A是切面面积。
S是球面面积,V是球体积。

向量表示的点p到球心c的距离为给定距离r的点的集合,p为球面上点。另一种表示法:

算法实现
class Sphere
{
public:
Vector3D center; // 用一个球心和半径表示球
float radius;
};3. AABB

AABB有8个顶点坐标,AABB内部点坐标都在[xmin,ymin,zmin]和[xmax,ymax,zmax]内部;
Pmin是坐标值最小的, Pmax是坐标值最大的;
c是AABB中心;
s是AABB的大小,使用向量表示;
r是AABB的大小的一半。
算法实现
class AABB3
{
Vector3 min;
Vector3 max;
Vector3 size() const (return max - min;);
float xSize() { return max.x - min.x; };
float xSize() { return max.x - min.x; };
float xSize() { return max.x - min.x; };
Vector3 center() { return (min + max) * 0.5f; };
Vector3 corner(int i) const; // 返回其中一个顶点
};
Vector3 Vector3::corner(int i) const
{
assert(i >= 0);
assert(i <= 7);
if (i == 0) return Vector3(min.x, min.y, min.z); // 左手坐标系
if (i == 1) return Vector3(max.x, min.y, min.z);
if (i == 2) return Vector3(min.x, max.y, min.z);
//...
}4. 平面

定义:点p到空间中的两个点q和r之间的距离相等的点的集合,组成的就是平面;
(1)使用两个向量p和n表示,p·n=d,如下。

其中向量p是平面上的任一点,n是单位向量(平面的法向量),两者向量点乘就是ax+by+cz=d;
d是平面到原点的距离。
平面的正面是法向量的方向。

(2)另一种定义平面常见做法是,使用平面上3个点p1,p2,p3,如下。

方向问题,是使用左手法则,大拇指指向法向量方向,其他指头的弯曲方向就是p1->p2->p3.
(3)多个点拟合一个最佳平面,先求法向量(nx,ny,nz),再求d即可,加上平面上的点p(x,y,z),则表示位pn=d;

(4)点到平面的距离a = qn - d

这样求点到平面的距离,只需要直到该点本身q,单位向量n和d即可。不需要求p.
5. 三角形
使用三个顶点表示三角形。
(1)边长和周长

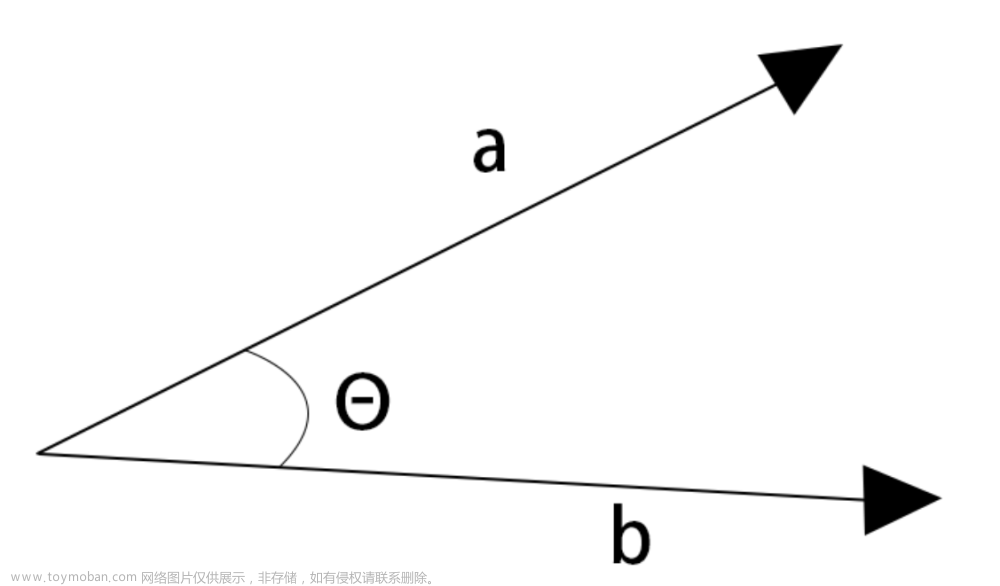
(2)正弦公式,正弦值和对面的边长比例

(3)余弦公式

(4) 面积
(1)已知底b和高h,则A = bh/2;
(2)已知边长,则使用海伦公式;
(3)只是知道三个顶点,则使用任意两条边向量的叉乘/2。

两条边叉乘的模长是平行四边形的面积。
6. 多边形

(1) 简单多边形,是内部没有点,按顺时针将边界点存储即可;
(2)复杂多边形,是内部有洞的,可以插入一个缝隙,使其变成简单多边形,再按顺时针访问边界点即可。

(3)凸多边形和凹多边形

所有的内角都小于180度,则是凸多边形 。文章来源:https://www.toymoban.com/news/detail-643127.html
参考:30.几何图元_哔哩哔哩_bilibili文章来源地址https://www.toymoban.com/news/detail-643127.html
到了这里,关于《3D 数学基础》12 几何图元的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!