算法通关村——透彻理解二分查找-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法通关村——透彻理解二分查找。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

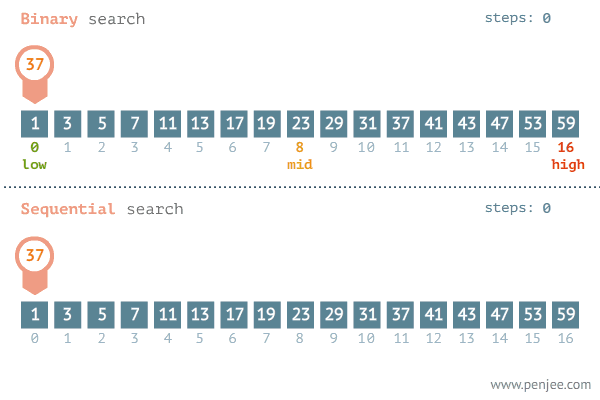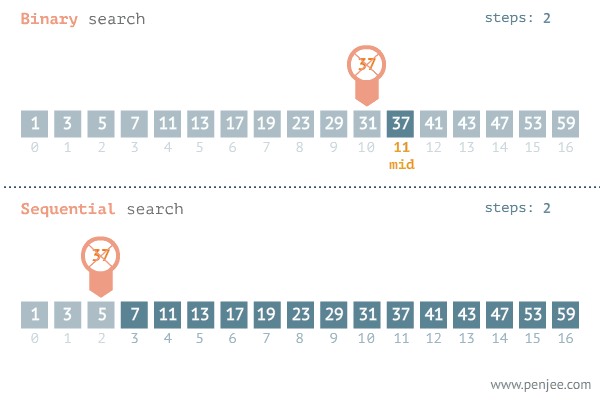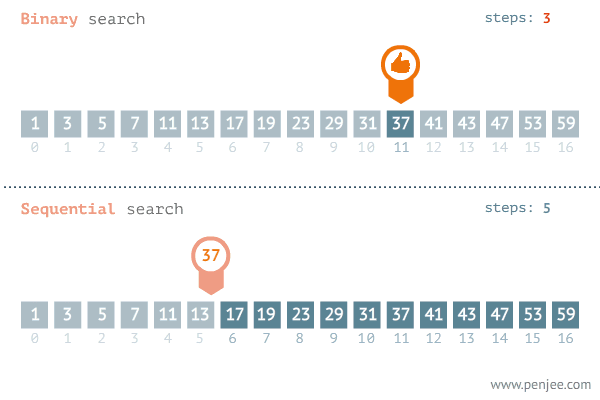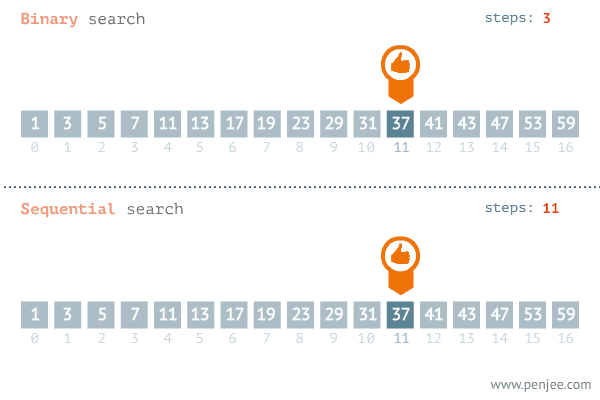
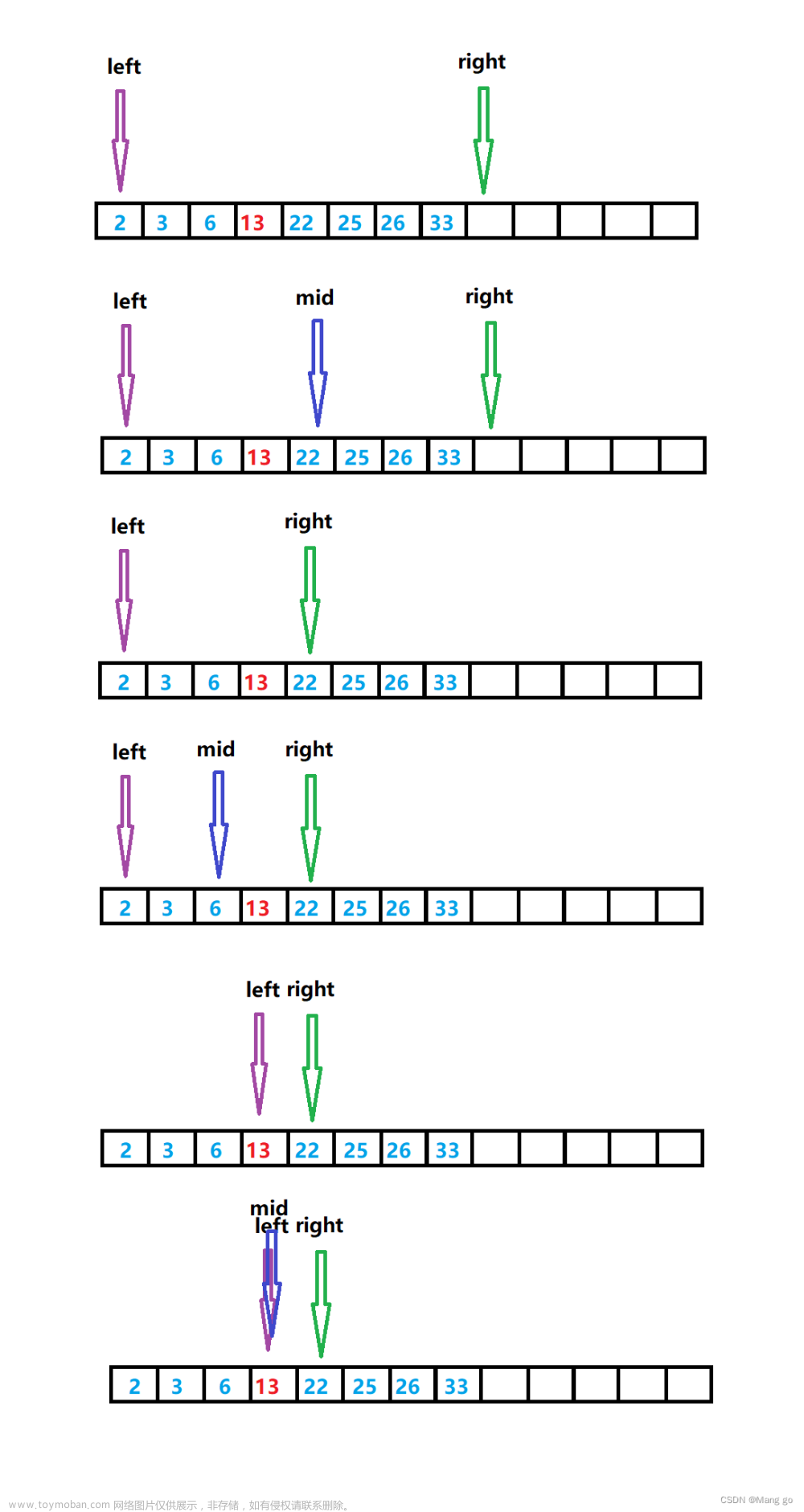
1. 循环法

    public static int binarySearch(int[] arr, int low, int high, int target) {
        while (low <= high) {
            // 这样写主要是避免溢出的情况，以及>>优先级小于+，避免出现死循环
            int mid = low + ((high - low) >> 1);
            if (arr[mid] == target) {
                return mid;
            } else if (arr[mid] < target) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return -1;
    }

2. 递归

    public static int binarySearch1(int[] array, int low, int high, int target) {
        if (low < high) {
            int mid = low + ((high - low) >> 1);
            if (array[mid] == target) {
                return mid;
            } else if (array[mid] > target) {
                return binarySearch(array, low, mid - 1, target);
            } else {
                return binarySearch(array, mid + 1, high, target);
            }
        }
        return -1;
    }

3. 元素中有重复的二分查找

假设现在有个数组里面有重复元素，并且按照增序排列，如果有相同元素，返回最左侧的第一个重复元素的位置。

核心思路也是比较简单了，当找到第一个重复的元素时候，记录位置，然后向左移动，左边的不是目标元素，就意味着左边没有重复的目标元素，然后+1就是目标元素的位置文章来源地址https://www.toymoban.com/news/detail-643569.html

 public static int search(int[] nums, int target) {
        if (nums == null || nums.length == 0)
            return -1;
        int low = 0;
        int high = nums.length - 1;
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            if (nums[mid] < target) {
                low = mid + 1;
            } else if (nums[mid] > target) {
                high = mid - 1;
            } else {
                // 找到了符合目标元素的数据位置,然后一直往左遍历，知道不是目标元素或者索引为0的时候停止
                while (mid != 0 && nums[mid] == target) {
                    mid--;
                }
                if (mid == 0 && nums[mid] == target) {
                    return mid;
                }
                return mid + 1;
            }
        }
        return -1;
    }