高精度除法【c++实现】超详细讲解-Toy模板网

这篇具有很好参考价值的文章主要介绍了高精度除法【c++实现】超详细讲解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

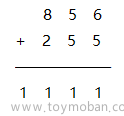
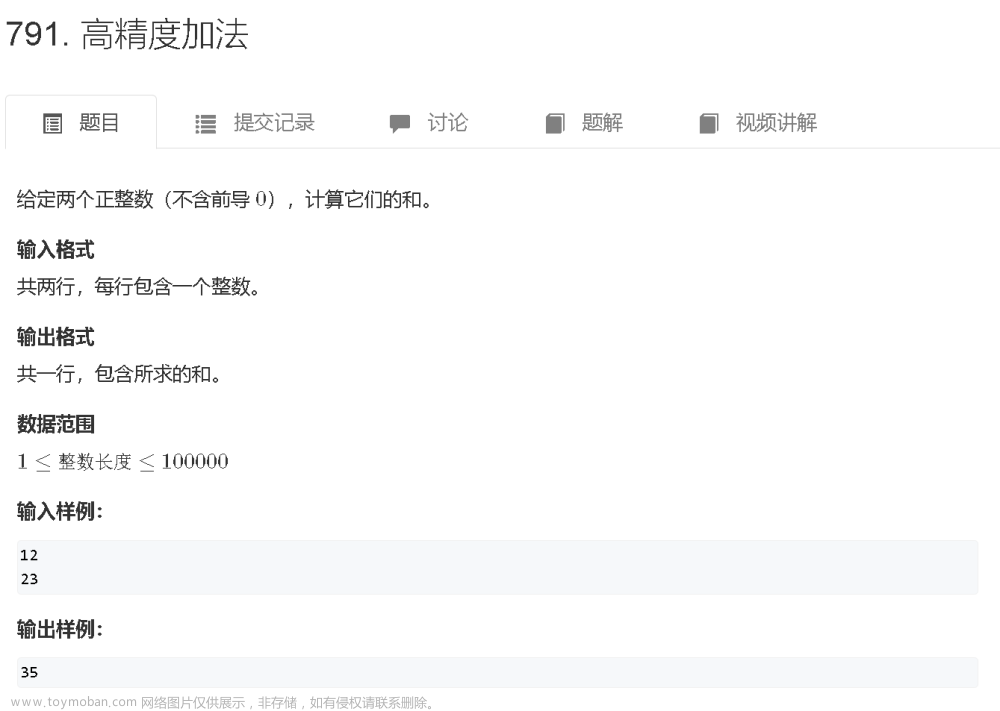
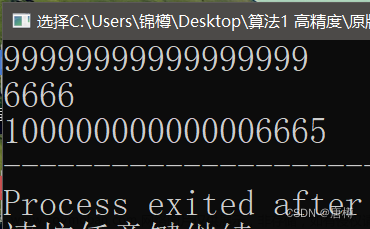
分类

高精度算法分为两种，高精除以低精和高精除以高精。不要看都是除法，就认为原理类似，其实是有很大差距的。让我们一起来学习吧！

有句话说在前面，如果除数等于0，就不要算了，不成立。（~~如果你忘了这个知识，小学数学老师饶不了你~~）

高精除以低精

高精度除低精度，原理是模拟竖式除法，和高精度其他算法一样都可以手动计算来感受一下实现方法。下面来一个较为简单的例子：1532 ÷ 21 = 72......20

步骤

第一步：

yu = 1

ans				1/21 = 0
a	2	3	5	1
b				21

第二步：

yu = 15

ans			15/21 = 0	0
a	2	3	5	1
b			21

第三步：

yu = 153

ans		153/21=7	0	0
a	2	3	5	1
b		21

第四步：

yu = 62

ans	62/21 = 2	7	0	0
a	2	3	5	1
b	21

第五步：

yu = 20文章来源地址https://www.toymoban.com/news/detail-643808.html

ans	2	7	0	0
a	2	3	5	1
b	21

核心代码

	//核心代码 
	for(int i = lena - 1; i >= 0; i--)
	{
		yu = yu * 10 + a[i];//模拟竖式除法中的落位 
		result[i] = yu / b;
		yu %= b;
	}

完整代码

#pragma GCC optimize(3)
#pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
string a1;
int b, yu;//b为除数 
int a[N], result[N];//a为被除数，result为结果 
int main()
{
	cin >> a1 >> b;
	int lena = a1.size();
	//倒序存储 
	for(int i = 0; i < lena; i++)
	{
		a[i] = a1[lena - i - 1] - '0';
	}
	//核心代码 
	for(int i = lena - 1; i >= 0; i--)
	{
		yu = yu * 10 + a[i];//模拟竖式除法中的落位 
		result[i] = yu / b;
		yu %= b;
	}
	//去除前缀多余的0 
	int tmp = lena;
	while(result[tmp] == 0 && tmp > 0) tmp--;
	//倒序输出 
	for(int i = tmp; i >= 0; i--) cout << result[i];
	cout << endl;
	cout << yu << endl; 
    return 0;
}

到了这里，关于高精度除法【c++实现】超详细讲解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！