一、问题的提出
n阶Z形矩阵的特点是按照之(Z)字形的方式排列元素。n阶Z形矩阵是指矩阵的大小为n×n，其中n为正整数。
题目描述
一个 n 行 n 列的螺旋(Z形)矩阵如图1所示，观察并找出填数规律。
图1 7行7列和8行8列的螺旋(Z形)矩阵
现在给出矩阵大小 n，请你输出该矩阵。
输入格式
输入一个整数 n(1≤n≤1000)，表示矩阵大小。
输出格式
输出 n 行 n 列，表示所求的矩阵。
输入输出样例
二、解决的思路
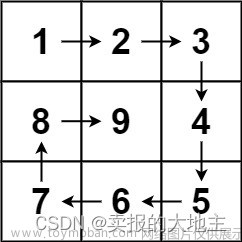
图2 矩阵生成原理图
根据题目描述、样例和图2可知：矩阵为n×n，其中偶数行(第一行为0行)从左向右排列元素；奇数行(第一行为0行)从右向左排列元素。
三、矩阵生成算法
n行n列，偶数行(第一行为0行)从0~n-1生成元素；奇数行(第一行为0行)从n-1~0生成元素。
程序代码如下：
N = 5
def prt(b): # 打印二维列表
for i in range(N):
for j in range(N):
print("%3d" % b[i][j], end='')
print()
def Helix_MatrixII(n):
cnt = 1
for i in range(n): # 生成n行
if i % 2 == 0: # 偶数行
for j in range(n): # 由左向右(j为0~n-1)生成
matrix[i][j] = cnt
cnt += 1
else: # 奇数行
for j in range(n): # 由右向左(j为n-1~0)生成
matrix[i][n-1-j] = cnt
cnt += 1
matrix = [] # 初始化二维矩阵matrix(二维列表)
for i in range(N):
matrix.append([])
for j in range(N):
matrix[i].append(0)
Helix_MatrixII(N)
prt(matrix)执行结果：
| 1 | 2 | 3 | 4 | 5 |
| 10 | 9 | 8 | 7 | 6 |
| 11 | 12 | 13 | 14 | 15 |
| 20 | 19 | 18 | 17 | 16 |
| 21 | 22 | 23 | 24 | 25 |
四、题目求解算法
按题目要求：输入矩阵大小 n，输出该矩阵。
def prt(b): # 打印二维列表
for i in range(N):
for j in range(N):
print("%3d" % b[i][j], end='')
print()
def Helix_MatrixII(n):
cnt = 1
for i in range(n): # 生成n行
if i % 2 == 0: # 偶数行
for j in range(n): # 由左向右(0~n-1)生成
matrix[i][j] = cnt
cnt += 1
else: # 奇数行
for j in range(n): # 由左向右(n-1~0)生成
matrix[i][n-1-j] = cnt
cnt += 1
N = int(input())
matrix = [] # 初始化二维矩阵matrix(二维列表)
for i in range(N):
matrix.append([])
for j in range(N):
matrix[i].append(0)
Helix_MatrixII(N)
prt(matrix)输入8，输出为文章来源：https://www.toymoban.com/news/detail-644400.html
文章来源地址https://www.toymoban.com/news/detail-644400.html
到了这里，关于【算法题】螺旋矩阵II (求解n阶Z形矩阵)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
