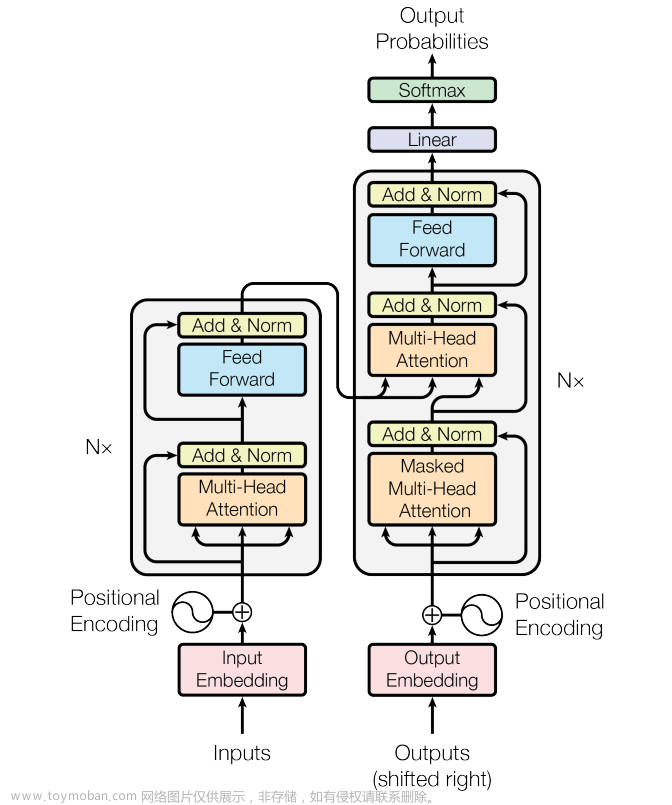
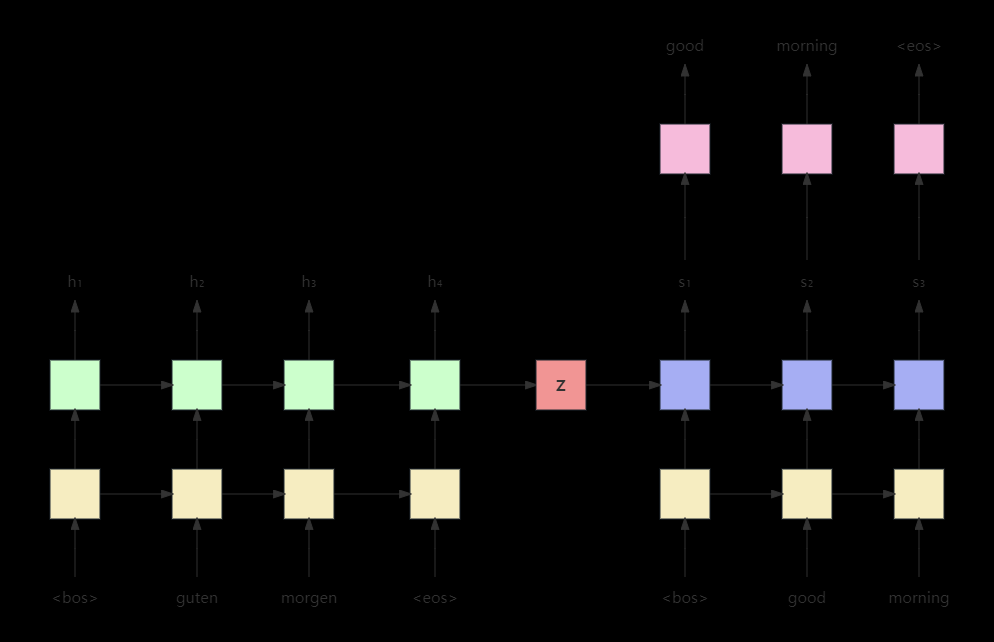
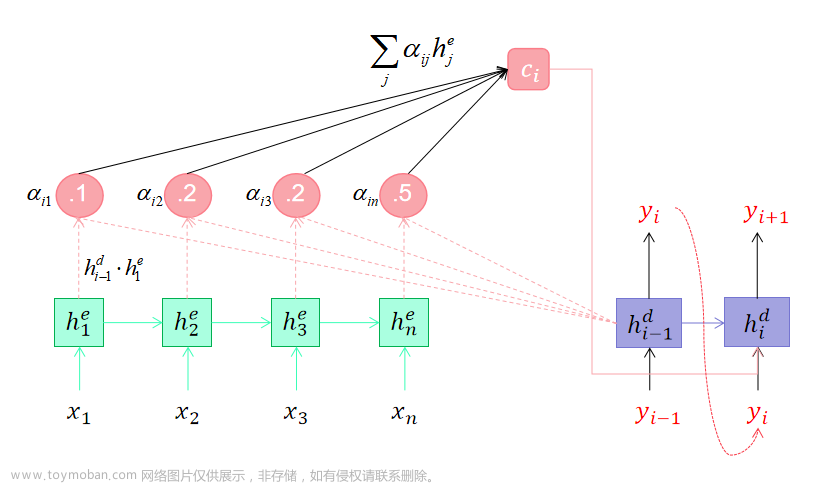
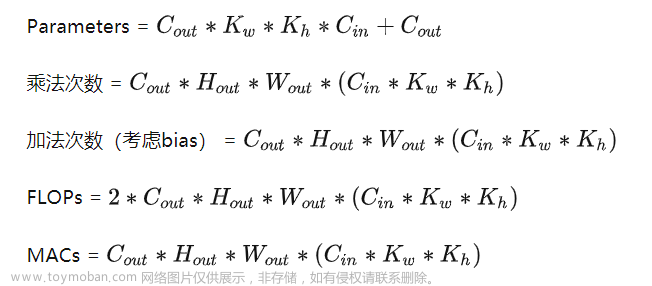从零构建深度学习推理框架-7 计算图的表达式-Toy模板网

这篇具有很好参考价值的文章主要介绍了从零构建深度学习推理框架-7 计算图的表达式。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

什么是表达式

表达式就是一个计算过程,类似于如下：

output_mid = input1 + input2
output = output_mid * input3

用图形来表达就是这样的。

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

但是在PNNX的表达式（Experssion Layer）中不是这个样子，而是以一种抽象得方式，替换掉输入张量改为@1,@2等等

所以上面的计算图也就变成了

add(@0,mul(@1,@2))

我们是希望把这个抽象的表达式变回到一个方便后端执行的计算过程（抽象的语法树来表达，在推理的时候转为逆波兰式）。

其中add和mul表示我们上一节中说到的RuntimeOperator, @0和@1表示我们上一节课中说道的RuntimeOperand. 这个抽象表达式看起来比较简单,但是实际上情况会非常复杂,我们给出一个复杂的例子：

add(add(mul(@0,@1),mul(@2,add(add(add(@0,@2),@3),@4))),@5)

这就要求我们需要一个鲁棒的表达式解析和语法树构建功能。

词法解析：

词法解析的目的就是将add(@0,mul(@1,@2))拆分为多个token,token依次为add ( @0 , mul等.代码如下：

enum class TokenType {
  TokenUnknown = -1,
  TokenInputNumber = 0,
  TokenComma = 1,
  TokenAdd = 2,
  TokenMul = 3,
  TokenLeftBracket = 4,
  TokenRightBracket = 5,
};

struct Token {
  TokenType token_type = TokenType::TokenUnknown;
  int32_t start_pos = 0; //词语开始的位置
  int32_t end_pos = 0; // 词语结束的位置

//比如add就是 start_pos = 0 , end_pos = 2
  
Token(TokenType token_type, int32_t start_pos, int32_t end_pos): token_type(token_type), start_pos(start_pos), end_pos(end_pos) {

  }
};

我们在TokenType中规定了Token的类型,类型有输入、加法、乘法以及左右括号等.Token类中记录了类型以及Token在字符串的起始和结束位置.

这样就把表达式变成了多个token的一个数组。

如下的代码是具体的解析过程,我们将输入（也就是：add(@0,mul(@1,@2))）存放在statement_中,首先是判断statement_是否为空, 随后删除表达式中的所有空格和制表符。

if (!need_retoken && !this->tokens_.empty()) {
    return;
  }

  CHECK(!statement_.empty()) << "The input statement is empty!";
  statement_.erase(std::remove_if(statement_.begin(), statement_.end(), [](char c) {
    return std::isspace(c);
  }), statement_.end());
  CHECK(!statement_.empty()) << "The input statement is empty!";

然后对于statement，我们遍历所有的表达式，要开始将这个statement拆成多个token啦！。



for (int32_t i = 0; i < statement_.size();) {
    char c = statement_.at(i);
    if (c == 'a') {
      CHECK(i + 1 < statement_.size() && statement_.at(i + 1) == 'd')
              << "Parse add token failed, illegal character: " << c;
      CHECK(i + 2 < statement_.size() && statement_.at(i + 2) == 'd')
              << "Parse add token failed, illegal character: " << c;
      Token token(TokenType::TokenAdd, i, i + 3);
      tokens_.push_back(token);
      std::string token_operation = std::string(statement_.begin() + i, statement_.begin() + i + 3);
      token_strs_.push_back(token_operation);
      i = i + 3;
    } 
 }

char c就是当前的字符如果这个等于a的话，那么由于我们的词法规定了以a开头的只有add，所以我们必须判断接下来的两个字符是不是'd','d',如果不是的话就报错，如果是的话就初始化一个新token保存。

同理：

else if (c == 'm') {
      CHECK(i + 1 < statement_.size() && statement_.at(i + 1) == 'u')
              << "Parse add token failed, illegal character: " << c;
      CHECK(i + 2 < statement_.size() && statement_.at(i + 2) == 'l')
              << "Parse add token failed, illegal character: " << c;
      Token token(TokenType::TokenMul, i, i + 3);
      tokens_.push_back(token);
      std::string token_operation = std::string(statement_.begin() + i, statement_.begin() + i + 3);
      token_strs_.push_back(token_operation);
      i = i + 3;
    }

也只有mul这一种可能。

如果是一个操作数的话：

else if (c == '@') {
      CHECK(i + 1 < statement_.size() && std::isdigit(statement_.at(i + 1)))
              << "Parse number token failed, illegal character: " << c;
      int32_t j = i + 1;
      for (; j < statement_.size(); ++j) {
        if (!std::isdigit(statement_.at(j))) {
          break;
        }
      }
      Token token(TokenType::TokenInputNumber, i, j);
      CHECK(token.start_pos < token.end_pos);
      tokens_.push_back(token);
      std::string token_input_number = std::string(statement_.begin() + i, statement_.begin() + j);
      token_strs_.push_back(token_input_number);
      i = j;
    }

那就是在@后只要是数字就一直读。读完之后组成新的token。

else if (c == ',') {
      Token token(TokenType::TokenComma, i, i + 1);
      tokens_.push_back(token);
      std::string token_comma = std::string(statement_.begin() + i, statement_.begin() + i + 1);
      token_strs_.push_back(token_comma);
      i += 1;
    } else if (c == '(') {
      Token token(TokenType::TokenLeftBracket, i, i + 1);
      tokens_.push_back(token);
      std::string token_left_bracket = std::string(statement_.begin() + i, statement_.begin() + i + 1);
      token_strs_.push_back(token_left_bracket);
      i += 1;
    } else if (c == ')') {
      Token token(TokenType::TokenRightBracket, i, i + 1);
      tokens_.push_back(token);
      std::string token_right_bracket = std::string(statement_.begin() + i, statement_.begin() + i + 1);
      token_strs_.push_back(token_right_bracket);
      i += 1;
    } else {
      LOG(FATAL) << "Unknown  illegal character: " << c;
    }

其他输入符也是如此。要是不再我们所列的项当中就报错。

这样我们就可以得到一个抽象的语法树。

语法解析：

语法解析的过程是递归向下的,定义在Generate_函数中.

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

通过这个语法树中序遍历left、right就可以得到具体的一个计算的过程。0 mul 1 add 0 mul 1

我们这里用一个例子来讲解：

add(@0,@1)这个例子.输入到Generate_函数中, 是一个token数组.

Generate_数组首先检查第一个输入是否为add,mul或者是input number中的一种.

CHECK(current_token.token_type == TokenType::TokenInputNumber|| 
current_token.token_type == TokenType::TokenAdd || current_token.token_type == TokenType::TokenMul);

那这里为什么不判断第一个不是left bracket token（左括号）或）（右括号）呢？

因为这个一般只会是以add，mul或者光一个数字@0。

第一个输入add,所以我们需要判断其后是否是left bracket来判断合法性, 如果合法则构建左子树.

else if (current_token.token_type == TokenType::TokenMul || current_token.token_type == TokenType::TokenAdd) {
    std::shared_ptr<TokenNode> current_node = std::make_shared<TokenNode>();//组枝起来一个节点
    current_node->num_index = -int(current_token.token_type);

    index += 1;//到左括号 因为add之后的的token一定到左括号 不对就报错
    CHECK(index < this->tokens_.size());
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenLeftBracket);

    index += 1;//左括号之后一定是一个操作数
    CHECK(index < this->tokens_.size());
    const auto left_token = this->tokens_.at(index);
    //token当前是@0这个token
    if (left_token.token_type == TokenType::TokenInputNumber
        || left_token.token_type == TokenType::TokenAdd || left_token.token_type == TokenType::TokenMul) {
//递归调用
      current_node->left = Generate_(index);
    }

处理下一个token, 构建左子树.

if (current_token.token_type == TokenType::TokenInputNumber) {
    uint32_t start_pos = current_token.start_pos + 1;
    uint32_t end_pos = current_token.end_pos;
    CHECK(end_pos > start_pos);
    CHECK(end_pos <= this->statement_.length());
    const std::string &str_number =
        std::string(this->statement_.begin() + start_pos, this->statement_.begin() + end_pos);
    return std::make_shared<TokenNode>(std::stoi(str_number), nullptr, nullptr);

  }

递归进入左子树后，判断是TokenType::TokenInputNumber则返回一个新的TokenNode到add token成为左子树.

检查下一个token是否为逗号，也就是在add(@0,@1)的@0是否为,

CHECK(this->tokens_.at(index).token_type == TokenType::TokenComma);

    index += 1;
    CHECK(index < this->tokens_.size());

下一步是构建add token的右子树

index += 1;
    CHECK(index < this->tokens_.size());
    const auto right_token = this->tokens_.at(index);
    if (right_token.token_type == TokenType::TokenInputNumber
        || right_token.token_type == TokenType::TokenAdd || right_token.token_type == TokenType::TokenMul) {
      current_node->right = Generate_(index);
    } else {
      LOG(FATAL) << "Unknown token type: " << int(left_token.token_type);
    }

    index += 1;
    CHECK(index < this->tokens_.size());
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenRightBracket);
    return current_node;
current_node->right = Generate_(index); /// 构建add(@0,@1)中的右子树

Generate_(index)递归进入后遇到的token是@1 token,因为是Input Number类型所在构造TokenNode后返回.

if (current_token.token_type == TokenType::TokenInputNumber) {
    uint32_t start_pos = current_token.start_pos + 1;
    uint32_t end_pos = current_token.end_pos;
    CHECK(end_pos > start_pos);
    CHECK(end_pos <= this->statement_.length());
    const std::string &str_number =
        std::string(this->statement_.begin() + start_pos, this->statement_.begin() + end_pos);
    return std::make_shared<TokenNode>(std::stoi(str_number), nullptr, nullptr);

  }

之后检查右括号在不在：

index += 1;
    CHECK(index < this->tokens_.size());
    CHECK(this->tokens_.at(index).token_type == TokenType::TokenRightBracket);
    return current_node;
  } else {
    LOG(FATAL) << "Unknown token type: " << int(current_token.token_type);
  }

至此, add语句的抽象语法树构建完成.

struct TokenNode {
  int32_t num_index = -1;
  std::shared_ptr<TokenNode> left = nullptr;
  std::shared_ptr<TokenNode> right = nullptr;
  TokenNode(int32_t num_index, std::shared_ptr<TokenNode> left, std::shared_ptr<TokenNode> right);
  TokenNode() = default;
};

在上述结构中, left存放的是@0表示的节点, right存放的是@1表示的节点

我们再弄一个更复杂一些的例子：

add(mul(@0,@1),@2)

add

(

mul

(

@0

,

@1

)

,

@2

)

index = 0, 当前遇到的token为add, 调用层为1

index = 1, 根据以上的流程,我们期待add token之后的token为left bracket, 否则就报错. 调用层为1

开始递归调用,构建add的左子树.从层1进入层2

index = 2, 遇到了mul token. 调用层为2.

index = 3, 根据以上的流程,我们期待mul token之后的token是第二个left bracket. 调用层为2.

开始递归调用用来构建mul token的左子树.

index = 4, 遇到@0,进入递归调用,进入层3, 但是因为操作数都是叶子节点,构建好之后就直接返回了,得到mul token的左子节点.放在mul token的left指针上.

index = 5, 我们希望遇到一个逗号,否则就报错mul(@0,@1)中中间的逗号.调用层为2.

index = 6, 遇到@2,进入递归调用,进入层3, 但是因为操作数是叶子节点, 构建好之后就直接返回到2,得到mul token的右子节点.

index = 7, 我们希望遇到一个右括号,就是mul(@1,@2)中的右括号.调用层为2.

到现在为止mul token已经构建完毕,返回形成add token的左子节点,add token的left指针指向构建完毕的mul树. 返回到调用层1.
...

add token开始构建right token,但是因为@2是一个输入操作数,所以直接递归就返回了,至此得到add的右子树,并用right指针指向.

这个东西最厉害的地方就在于，括号里面一定是一个新的节点！

Experssion Layer的实现（如何实现@0 + @1）：

Expression Operator的定义

class ExpressionOp : public Operator {
 public:
  explicit ExpressionOp(const std::string &expr);
  std::vector<std::shared_ptr<TokenNode>> Generate();

 private:
  std::unique_ptr<ExpressionParser> parser_;
  std::vector<std::shared_ptr<TokenNode>> nodes_;
  std::string expr_;
};

其中expr_表示表达式字符串, nodes_表示经过逆波兰变换之后得到的节点.

Expression Layer的定义

class ExpressionLayer : public Layer {
 public:
  explicit ExpressionLayer(const std::shared_ptr<Operator> &op);
  void Forwards(const std::vector<std::shared_ptr<Tensor<float>>> &inputs,
                std::vector<std::shared_ptr<Tensor<float>>> &outputs) override;
 private:
  std::unique_ptr<ExpressionOp> op_;
};

初始化Expression Layer

ExpressionLayer::ExpressionLayer(const std::shared_ptr<Operator> &op) : Layer("Expression") {
  CHECK(op != nullptr && op->op_type_ == OpType::kOperatorExpression);
  ExpressionOp *expression_op = dynamic_cast<ExpressionOp *>(op.get());

  CHECK(expression_op != nullptr) << "Expression operator is empty";
  this->op_ = std::make_unique<ExpressionOp>(*expression_op);
}

Expression Layer中的输入排布

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

在Expression Layer的输入中, 多个输入依次排布. 如果batch_size的大小为4, 则上图中input1中的元素数量为4, input2的元素数量也为4. 换句话说, input1中的数据都来源于操作数1(operand 1), input2中的数据都来源于操作数2(operand 2).

将数据存放到input1和input2的实现如下:

int batch_size = 4;
  for (int i = 0; i < batch_size; ++i) {
    std::shared_ptr<ftensor> input = std::make_shared<ftensor>(3, 224, 224);
    input->Fill(1.f);
    inputs.push_back(input);
  }

  for (int i = 0; i < batch_size; ++i) {
    std::shared_ptr<ftensor> input = std::make_shared<ftensor>(3, 224, 224);
    input->Fill(2.f);
    inputs.push_back(input);
  }

inputs被分为两段, 前半段存放input1, 前半段的长度为4. 后半段存放input2, 后半段的长度为4.

计算的结果存放在outputs, 8个输入数据两两相加, 最后的输出数据大小等于4.

Expression Layer的计算过程

数据排布

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

第一个例子

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

已知有如上的数据存储排布, 在本节中我们将讨论如何根据现有的数据完成add(@0,@1)计算. 可以看到每一次计算的时候, 都以此从input1和input2中取得一个数据进行加法操作, 并存放在对应的输出位置.

第二个例子

下图的例子展示了对于三个输入,mul(add(@0,@1),@2)的情况:

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

每次计算的时候依次从input1, input2和input3中取出数据, 并作出相应的运算, 并将结果数据存放于对应的output中.

操作数处理的代码实现

在ExpressionLayer::Forward函数中, 首先检查输入是否为空, 并初始化outputs数组中的元素.

CHECK(!inputs.empty());

  const uint32_t batch_size = outputs.size();
  CHECK(batch_size != 0);

  for (uint32_t i = 0; i < batch_size; ++i) {
    CHECK(outputs.at(i) != nullptr && !outputs.at(i)->empty());
    outputs.at(i)->Fill(0.f);
  }

  CHECK(this->op_ != nullptr && this->op_->op_type_ == OpType::kOperatorExpression);
  std::stack<std::vector<std::shared_ptr<Tensor<float>>>> op_stack;
  const std::vector<std::shared_ptr<TokenNode>> &token_nodes = this->op_->Generate();

this->op_->Generate(); 获得的是逆波兰表达式.

for (const auto &token_node : token_nodes) {
    if (token_node->num_index >= 0) {
      uint32_t start_pos = token_node->num_index * batch_size;
      std::vector<std::shared_ptr<Tensor<float>>> input_token_nodes;
      for (uint32_t i = 0; i < batch_size; ++i) {
        CHECK(i + start_pos < inputs.size());
        input_token_nodes.push_back(inputs.at(i + start_pos));
      }
      op_stack.push(input_token_nodes);
    }
  }

依次遍历逆波兰表达式, 如果当前的op遇到的是一个操作数, 例如@0或者@1. 就将他们一个批次的数据(input_token_nodes)全部读取出来, 并临时存放到栈op_stack中.

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

举个例子, 对于input1就将input1中所有的数据读取出来并存放到input_token_nodes中, 再将input_token_nodes这一个批次的数据放入到栈中.

根据输入的逆波兰式@0,@1,add,遇到的第一个节点是操作数是@0, 所以栈op_stack内的内存布局如下:

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

当根据顺序遇到第二个节点(op)的时候, 操作数@1的时候, 再将inputs中的操作数读取出来并存放到input_token_nodes中, 再将input_token_nodes这一个批次的数据放入到栈中.

从零构建深度学习推理框架-7 计算图的表达式,Infer,深度学习,人工智能

运算符处理的代码实现

const int32_t op = token_node->num_index;
      CHECK(op_stack.size() >= 2) << "The number of operand is less than two";
      std::vector<std::shared_ptr<Tensor<float>>> input_node1 = op_stack.top();

      CHECK(input_node1.size() == batch_size);
      op_stack.pop();

      std::vector<std::shared_ptr<Tensor<float>>> input_node2 = op_stack.top();
      CHECK(input_node2.size() == batch_size);
      op_stack.pop();

当节点(op)类型为操作符号的时候, 首先弹出栈(op_stack)内的两个批次操作数, 对于如上的情况input_node1分别存放input1...4, input_node2分别存放input5...8.

CHECK(input_node1.size() == input_node2.size());
      std::vector<std::shared_ptr<Tensor<float>>> output_token_nodes(batch_size);
      for (uint32_t i = 0; i < batch_size; ++i) {
        if (op == -int(TokenType::TokenAdd)) {
          output_token_nodes.at(i) = ftensor::ElementAdd(input_node1.at(i), input_node2.at(i));
        } else if (op == -int(TokenType::TokenMul)) {
          output_token_nodes.at(i) = ftensor::ElementMultiply(input_node1.at(i), input_node2.at(i));
        } else {
          LOG(FATAL) << "Unknown operator type: " << op;
        }
      }
      op_stack.push(output_token_nodes);

当获取大小长度为batch_size的input_node1和input_node2后, 流程在for(int i = 0...batch_size)中对两个输入进行两两操作, 操作类型定义于当前的op中. 对于逆波兰式@0,@1,add, 在如上处理完两个输入节点之后,当前的节点类型是add.

文章来源地址https://www.toymoban.com/news/detail-644558.html

到了这里，关于从零构建深度学习推理框架-7 计算图的表达式的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！