前言
约瑟夫环是一个古老而有趣的问题,它涉及人与人之间的生死较量,引发了人们长久以来的思考和探索。这个问题可以通过不同的方式来解决,每种方式都有其独特的优缺点。
使用数组实现约瑟夫环可以简单直观地表示人员的顺序,但受到数组大小静态限制和数据复制的操作效率较低的影响。而使用单链表实现则可以在运行时动态调整约瑟夫环的大小,并通过指针更新来实现删除节点,从而提高效率。
另外,通过数学公式来解决约瑟夫环问题更加高效,无需构建和遍历数据结构,只需通过简单的数学计算就能得到最后幸存者的编号。这种方法适用于规模较大的问题,并且具有极高的效率。
每种实现方式都有其独特的优点,选择合适的方式取决于实际需求。无论使用哪种方式,解决约瑟夫环问题都需要运用数学思维和编程技巧,同时激发人们对数学和算法的兴趣和探索精神。
约瑟夫环的历史背景
约瑟夫环(Josephus problem)是一个古老的数学问题,名字来源于古代犹太历史学家弗拉维奥·约瑟夫斯(Flavius Josephus)。根据传说,约瑟夫斯是一名犹太军事将领,他在一次由罗马人围困的犹太要塞中被困。
根据传统的约瑟夫斯的记载,他和他的39个同胞被困在一个洞穴里。作为最后一人,他们决定宁愿自杀也不愿成为罗马人的俘虏。于是,他们决定站成一个圆圈,从一个人开始数数,每数到一个指定的数字就将该人杀死,然后再从下一个人开始数。这样一直进行下去,直到只剩下一个人,他将成为唯一的幸存者。
这个问题的核心是决定哪一个位置是最后的幸存者。约瑟夫斯根据自己的回忆和经验给出了一个解决方案。根据他的描述,他站在第七个位置,也就是说,在圆圈中数到第七个人时,他将成为最后的幸存者。
数组方法解决
当使用C语言来实现约瑟夫环时,可以利用数组来表示人员的顺序,以及通过循环和条件语句来模拟杀人的过程。下面是一个详细的解释:
#include <stdio.h>
#define MAX_SIZE 100
// 约瑟夫环函数
int josephus(int n, int k)
{
int circle[MAX_SIZE]; // 用数组表示约瑟夫环
int i, index, count;
// 初始化约瑟夫环
for (i = 0; i < n; ++i)
{
circle[i] = i + 1;
}
index = 0; // 从第一个人开始
count = 0; // 计数器
// 开始杀人循环,直到只剩下一个人
while (n > 1)
{
count++;
// 数到第k个人就杀掉他
if (count == k)
{
// 打印被杀的人的编号
printf("杀死第 %d 个人\n", circle[index]);
// 将被杀的人从约瑟夫环中移除
for (i = index; i < n - 1; ++i)
{
circle[i] = circle[i + 1];
}
count = 0; // 重置计数器
n--; // 约瑟夫环的人数减一
}
index++; // 移向下一个人
// 当到达约瑟夫环的末尾时,回到开始位置
if (index == n)
{
index = 0;
}
}
// 返回最后幸存者的编号
return circle[0];
}
int main()
{
int n, k;
int survivor;
printf("请输入约瑟夫环的人数n:");
scanf("%d", &n);
printf("请输入每次数的数字k:");
scanf("%d", &k);
survivor = josephus(n, k);
printf("最后幸存者的编号是:%d\n", survivor);
return 0;
}
在这段代码中,我们首先声明了一个数组circle来表示约瑟夫环,其大小为MAX_SIZE。然后,我们使用循环来初始化约瑟夫环中的人员,将它们从1到n依次排列。
接下来,我们使用index和count变量来模拟杀人的过程。index表示当前数到的人的位置,count表示已经数过的人数。
在杀人循环中,我们首先增加计数器count,然后检查是否数到第k个人。如果数到第k个人,我们将打印出被杀的人的编号,然后将他从约瑟夫环中移除。
移除人员后,我们需要将后面的人向前移动以填补空缺,并将约瑟夫环的人数减一。
最后,当只剩下一个人时,循环结束,我们将返回最后幸存者的编号。
在主函数中,我们接收用户输入的约瑟夫环的人数n和每次数的数字k,并调用josephus函数来计算最后幸存者的编号,并将其打印出来。
C语言单链表解决
当使用C语言来实现约瑟夫环时,也可以利用单链表来表示人员的顺序,以及通过循环和条件语句来模拟杀人的过程。下面是一个详细的解释:
#include <stdio.h>
#include <stdlib.h>
// 定义单链表节点结构
typedef struct Node
{
int data;
struct Node *next;
} Node;
// 创建一个单链表节点
Node *createNode(int data)
{
Node *newNode = (Node *)malloc(sizeof(Node));
newNode->data = data;
newNode->next = NULL;
return newNode;
}
// 创建约瑟夫环
Node *createJosephusCircle(int n)
{
Node *head = createNode(1);
Node *prev = head;
int i;
for (i = 2; i <= n; ++i)
{
Node *newNode = createNode(i);
prev->next = newNode;
prev = newNode;
}
prev->next = head; // 将末尾节点指向头节点形成循环
return head;
}
// 模拟杀人过程
int josephus(int n, int k)
{
Node *head = createJosephusCircle(n);
Node *current = head;
Node *prev = NULL;
int count = 0;
while (head->next != head)
{
count++;
if (count == k)
{
printf("杀死第 %d 个人\n", current->data);
prev->next = current->next;
free(current);
current = prev->next;
count = 0;
}
else
{
prev = current;
current = current->next;
}
}
int survivor = head->data;
free(head);
return survivor;
}
int main()
{
int n, k;
int survivor;
printf("请输入约瑟夫环的人数n:");
scanf("%d", &n);
printf("请输入每次数的数字k:");
scanf("%d", &k);
survivor = josephus(n, k);
printf("最后幸存者的编号是:%d\n", survivor);
return 0;
}
在这段代码中,我们首先定义了一个单链表节点结构Node,包含一个data字段来存储人员编号,以及一个next指针指向下一个节点。
接着,我们定义了一个createNode函数来创建一个新的单链表节点,并返回指向该节点的指针。
然后,我们编写了一个createJosephusCircle函数来创建约瑟夫环。我们从1到n依次创建节点,并使用next指针将它们连接起来。最后,我们将末尾节点的next指针指向头节点,形成循环。
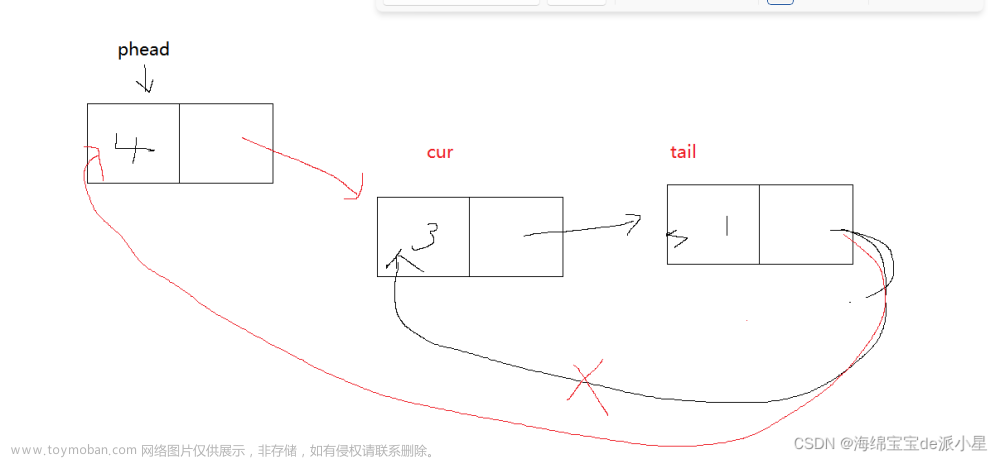
接下来,我们编写了josephus函数来模拟杀人的过程。我们使用current指针来追踪当前数到的人,使用prev指针来记录上一个节点,以便在杀人时更新链表。我们使用count变量来计数,当数到第k个人时,我们将打印出被杀的人的编号,并将其从链表中移除。
最后,我们将头节点的编号作为最后的幸存者,并释放内存。
在主函数中,我们接收用户输入的约瑟夫环的人数n和每次数的数字k,并调用josephus函数来计算最后幸存者的编号,并将其打印出来。
这就是使用单链表来实现约瑟夫环的C语言代码的详细解释。
数学公式(递归方法)
使用数学公式计算约瑟夫环的最后幸存者的编号,可以通过递归或迭代实现。下面是一个使用迭代方式的详细解释:
#include <stdio.h>
int josephus(int n, int k)
{
int survivor = 0;
int i;
// 从n=1的情况开始递推计算
for (i = 2; i <= n; ++i)
{
survivor = (survivor + k) % i;
}
// 因为编号从1开始,所以加1得到幸存者的编号
survivor += 1;
return survivor;
}
int main()
{
int n, k;
int survivor;
printf("请输入约瑟夫环的人数n:");
scanf("%d", &n);
printf("请输入每次数的数字k:");
scanf("%d", &k);
survivor = josephus(n, k);
printf("最后幸存者的编号是:%d\n", survivor);
return 0;
}
在这段代码中,我们定义了一个josephus函数,以参数n和k来表示约瑟夫环的人数和每次数的数字。
通过迭代的方式,我们从n=2开始,依次计算每个人被杀后下一个人的编号。我们使用一个变量survivor来追踪计算过程中的幸存者的编号,初始值为0。
在每一轮迭代中,我们将survivor加上k,然后对总人数i取模,得到下一个被杀的人的编号。这样,我们依次找到下一个被杀的人,直到只剩下最后一个人。
最后,我们将survivor加1,以匹配约瑟夫环的人员编号规则,然后返回最后幸存者的编号。
在主函数中,我们接收用户输入的约瑟夫环的人数n和每次数的数字k,并调用josephus函数来计算最后幸存者的编号,并将其打印出来。
这就是使用数学公式来实现约瑟夫环的C语言代码的详细解释。
总结这三种方式的优缺点以及可优化方案
下面总结了约瑟夫环的三种实现方式的优缺点,以及可能的优化方案:
1. 数组实现:
优点:
- 简单直观,易于理解和实现。
- 存储和访问速度快,由于直接使用数组索引,无需指针操作。
缺点:
- 数组的大小是静态的,需要在编译时确定,限制了约瑟夫环的规模。
- 当删除一个人后,需要将后面的人向前移动,这涉及到数据的大量复制操作,效率较低。
可优化方案:
- 使用动态数组或动态链表,以便在运行时根据需要调整约瑟夫环的大小。
2. 单链表实现:
优点:
- 动态分配内存,可以在运行时动态调整约瑟夫环的大小。
- 删除节点操作只需更新指针,效率较高。
缺点:
- 节点的访问需要通过遍历链表来实现,相比数组的随机访问效率较低。
- 链表节点需要额外的内存空间保存指针信息。
可优化方案:
- 使用双向链表,可以提高节点的访问效率。
3. 数学公式实现:
优点:
- 不需要构建和遍历约瑟夫环的数据结构,计算直接基于数学公式,效率非常高。
- 不受约瑟夫环规模的限制,适用于非常大的问题。
缺点:
- 只能得到最后幸存者的编号,无法得到被杀掉的人的顺序。
- 对于一些特殊的k值,可能会产生周期性的规律。
可优化方案:
- 无法通过简单的优化来改进数学公式的计算过程,因为已经是最优解。
总的来说,选择合适的实现方式取决于具体情况。如果约瑟夫环的规模较小且需求是得到完整的被杀人的顺序,可以选择数组或单链表实现。如果约瑟夫环的规模较大或仅需得到最后幸存者的编号,数学公式是最优解。另外,根据具体需求,还可以结合优化方案来提高实现的效率和灵活性。文章来源:https://www.toymoban.com/news/detail-644625.html
约瑟夫环问题的魅力在于它融合了数学、逻辑和编程,使人们在解题过程中不仅锻炼了思维能力,也体验到了数学和计算机科学的魅力。这个问题既是一种思维训练的机会,也是一次探索数学和算法的奇妙之旅。无论是在学术研究中还是日常生活中,约瑟夫环问题都能给我们带来乐趣和启发。文章来源地址https://www.toymoban.com/news/detail-644625.html
到了这里,关于神奇的约瑟夫环(C语言)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!