基于灰狼优化（GWO）、帝国竞争算法（ICA）和粒子群优化（PSO）对梯度下降法训练的神经网络的权值进行了改进（Matlab代码实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于灰狼优化（GWO）、帝国竞争算法（ICA）和粒子群优化（PSO）对梯度下降法训练的神经网络的权值进行了改进（Matlab代码实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

在神经网络训练中，使用传统的梯度下降法可能会受到局部极值问题的影响，导致训练结果不够稳定或收敛速度较慢。为了改进神经网络的权值训练，考虑结合灰狼优化（GWO）、帝国竞争算法（ICA）和粒子群优化（PSO）等优化算法。下面是方法：

初始化神经网络：首先，根据问题的特点和需求，设计并初始化神经网络的结构，包括神经元层、激活函数等。

梯度下降法训练：使用传统的梯度下降法对神经网络进行初始训练，以获得一个基本的权值设置。

算法集成：将灰狼优化（GWO）、帝国竞争算法（ICA）和粒子群优化（PSO）三种优化算法集成到神经网络的权值调整过程中。

多种算法运行：为了充分利用这些算法的优势，可以采取以下策略：

在每次权值更新之前，使用三种算法分别对神经网络权值进行优化，得到三组不同的权值。

将这三组权值分别代入神经网络进行预测或训练，得到对应的损失函数值。

根据损失函数值的大小，选择其中表现最好的一组权值来更新神经网络。

参数调整：每个优化算法都有一些参数需要调整，如迭代次数、种群大小等。您可以通过实验和交叉验证来选择最佳的参数组合，以达到更好的性能。

终止条件：设置合适的终止条件，如达到一定的迭代次数或损失函数值足够小。

结果分析：最后，比较集成了三种优化算法的权值训练方法与单独使用梯度下降法的效果。分析哪种方法在收敛速度、稳定性和精度方面表现更好。

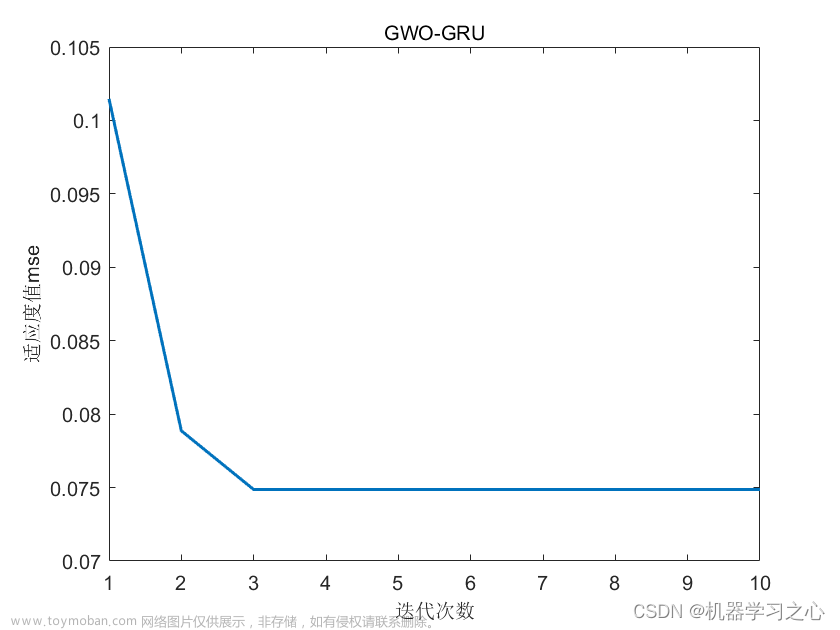
📚2 运行结果

基于灰狼优化（GWO）、帝国竞争算法（ICA）和粒子群优化（PSO）对梯度下降法训练的神经网络的权值进行了改进（Matlab代码实现）,算法,神经网络,matlab

主函数部分代码：

clc;
clear;
close all;

%% Problem Definition
%% loading dataset %%
load('Weight_mat.mat')
load('trainset.mat')
load('testset.mat')

var_num=71;            
VarSize=[1 var_num];  
VarMin=-5;        
VarMax= 5;       
%% PSO Parameters
max_epoch=100;      
ini_pop=50;        

% Constriction Coefficients
phi1=2.1;
phi2=2.1;
phi=phi1+phi2;
khi=2/(phi-2+sqrt(phi^2-4*phi));
w=khi;          % Inertia Weight
wdamp=0.99;        % Inertia Weight Damping Ratio
c1=khi*phi1;    % Personal Learning Coefficient
c2=khi*phi2;    % Global Learning Coefficient

% Velocity Limits
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
%% Initialization

empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];

particle=repmat(empty_particle,ini_pop,1);  
GlobalBest.Cost=inf;
Cost_Test= zeros(50,1);
for i=1:ini_pop
    
    % Initialize Position
    particle(i).Position= WEIGHTS(i ,:);
    
    % Initialize Velocity
    particle(i).Velocity=zeros(VarSize);
    
    % Evaluation
    particle(i).Cost=mape_calc(particle(i).Position,trainset);
    Cost_Test(i)=mape_calc(particle(i).Position,testset);
    % Update Personal Best
    particle(i).Best.Position=particle(i).Position;
    particle(i).Best.Cost=particle(i).Cost;
    
    % Update Global Best
    if particle(i).Best.Cost<GlobalBest.Cost
        
        GlobalBest=particle(i).Best;
        
    end
    
end

BestCost_Train=zeros(max_epoch,1);
BestCost_Test=zeros(max_epoch,1);
[~, SortOrder]=sort(Cost_Test);
Cost_Test =Cost_Test(SortOrder);
%% PSO Main Loop
for it=1:max_epoch
    for i=1:ini_pop
        % Update Velocity
        particle(i).Velocity = w*particle(i).Velocity ...
            +c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ...
            +c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position);
        
        % Apply Velocity Limits
        particle(i).Velocity = max(particle(i).Velocity,VelMin);
        particle(i).Velocity = min(particle(i).Velocity,VelMax);
        
        % Update Position
        particle(i).Position = particle(i).Position + particle(i).Velocity;
        IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
        particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
        
        % Apply Position Limits
        particle(i).Position = max(particle(i).Position,VarMin);
        particle(i).Position = min(particle(i).Position,VarMax);
        
        % Evaluation
        particle(i).Cost = mape_calc(particle(i).Position,trainset);
        for l= 1:ini_pop
          Cost_Test(l)=mape_calc(particle(l).Position,testset);
        end
        [~, SortOrder]=sort(Cost_Test);
        Cost_Test =Cost_Test(SortOrder);
        BestCost_Test(it) = Cost_Test(1);
        % Update Personal Best
        if particle(i).Cost<particle(i).Best.Cost
            
            particle(i).Best.Position=particle(i).Position;
            particle(i).Best.Cost=particle(i).Cost;
            
            % Update Global Best
            if particle(i).Best.Cost<GlobalBest.Cost
                
                GlobalBest=particle(i).Best;
                
            end
            
        end
        
    end