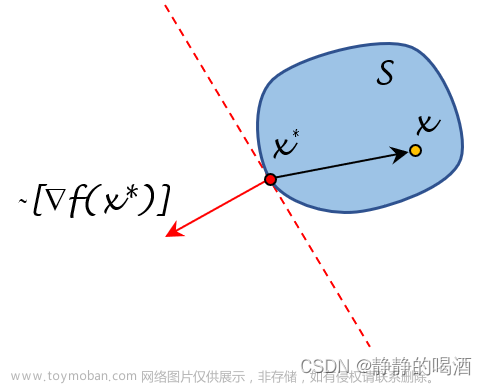
我们知道,若 f ( x ) f(x) f(x)在 R \text{ℝ} R上连续,则 f ( x ) f(x) f(x)有原函数 F ( x ) , x ∈ R F(x),x\in\text{ℝ} F(x),x∈R。因此,解方程 f ( x ) = 0 f(x)=0 f(x)=0,等价于计算 F ( x ) F(x) F(x)的局部最小(大)值。譬如,设 f ( x ) f(x) f(x)在 [ a 0 , b 0 ] [a_0,b_0] [a0,b0]上连续且 f ( a 0 ) ⋅ f ( b 0 ) < 0 f(a_0)\cdot f(b_0)<0 f(a0)⋅f(b0)<0,我们对解决局部优化问题的二分算法稍加修改即可用于在 ( a 0 , b 0 ) (a_0,b_0) (a0,b0)内解方程 f ( x ) = 0 f(x)=0 f(x)=0。
def bisect_solv(fun,bracket,eps=1e-10):
a0,b0=bracket #初始区间端点
a1=(a0+b0)/2 #区间中点
f=fun(a1) #当前函数值
k=1 #迭代次数
while (b0-a0>=eps) and (abs(f)>=eps): #循环迭代
if f*fun(a0)>0: #当前点函数值与左端点同号
a0=a1 #修改左端点
else: #否则
b0=a1 #修改右端点
a1=(a0+b0)/2 #当前中点
f=fun(a1) #当前点函数值
k+=1 #迭代次数
return a1,k
程序的第1~14行定义的函数bisect_solv实现解一元方程
f
(
x
)
=
0
f(x)=0
f(x)=0的二分算法。函数含有三个参数:fun表示连续函数
f
(
x
)
f(x)
f(x)。bracket表示初始区间
[
a
0
,
b
0
]
[a_0,b_0]
[a0,b0],这是一个二元组。要求
f
(
a
0
)
⋅
f
(
b
0
)
<
0
f(a_0)\cdot f(b_0)<0
f(a0)⋅f(b0)<0。eps表示容错误差
ε
\varepsilon
ε,缺省值为
1
0
−
10
10^{-10}
10−10。2~ 5行作初始化操作,第6~13行的while循环进行迭代,取区间中点
a
1
=
a
0
+
b
0
2
a_1=\frac{a_0+b_0}{2}
a1=2a0+b0,计算
f
1
=
f
(
a
1
)
f_1=f(a_1)
f1=f(a1),检测
f
1
f_1
f1是否与
f
(
a
0
)
f(a_0)
f(a0)同号,若是则修改
a
0
a_0
a0为
a
1
a_1
a1,否则修改
b
0
b_0
b0为
a
1
a_1
a1,以保持
f
(
a
0
)
f(a_0)
f(a0)与
f
(
b
0
)
f(b_0)
f(b0)异号。循环往复,直至
∣
f
(
a
1
)
∣
<
ε
|f(a_1)|<\varepsilon
∣f(a1)∣<ε或
∣
b
0
−
a
0
∣
<
ε
|b_0-a_0|<\varepsilon
∣b0−a0∣<ε为止。第14行返回方程解的近似值a1及迭代次数k。
例1:
ln
2
\ln{2}
ln2可视为方程
e
x
−
2
=
0
e^x-2=0
ex−2=0的解。给定初始区间
[
a
0
,
b
0
]
=
[
0
,
1
]
[a_0,b_0]=[0,1]
[a0,b0]=[0,1],容错误差
ε
=
1
0
−
10
\varepsilon=10^{-10}
ε=10−10,用二分法解方程
e
x
−
2
=
0
e^x-2=0
ex−2=0,以算得
ln
2
\ln{2}
ln2的近似值。
解:下列代码完成计算
f=lambda x: np.exp(x)-2 #设置函数f(x)
solution=bisect_solv(f,(0,1)) #求解f(x)=0在区间(0,1)内的根
print(solution)
程序的第1行设置函数 f ( x ) = e x − 2 f(x)=e^x-2 f(x)=ex−2,第2行调用bisect_solv计算 f ( x ) = 0 f(x)=0 f(x)=0在区间 ( 0 , 1 ) (0,1) (0,1)内的根。运行程序,输出:
(0.6931471806019545, 29)
这意味着用二分法在
ε
=
1
0
−
10
\varepsilon=10^{-10}
ε=10−10的容错误差下,迭代29次,算得
e
x
−
2
=
0
e^x-2=0
ex−2=0在
(
0
,
1
)
(0,1)
(0,1)内的根为0.6931,即
ln
2
\ln2
ln2的近似值为0.6931。
scipy的optimize模块提供了函数
root_
scalar(f, method, ...)
\text{root\_{}scalar(f, method, ...)}
root_scalar(f, method, ...)
用于一元方程的求根。参数f表示方程
f
(
x
)
=
0
f(x)=0
f(x)=0中的函数
f
(
x
)
f(x)
f(x)。method表示所用求根方法。返回值是包含收敛信息、函数调用次数、迭代次数及近似根等信息的元组。scipy.minimize为root_{}scalar的method参数提供了如下的可选方法
| 方法 | f的定义域 | 初始区间 | 1阶导数 | 2阶导数 | 收敛 | 收敛率 p p p |
|---|---|---|---|---|---|---|
| bisect | R | 必需 | 不限 | 不限 | 保证 | 1(线性) |
| brentq | R | 必需 | 不限 | 不限 | 保证 | 1 ≤ p ≤ 1.62 1\leq p\leq1.62 1≤p≤1.62 |
| brenth | R | 必需 | 不限 | 不限 | 保证 | 1 ≤ p ≤ 1.62 1\leq p\leq1.62 1≤p≤1.62 |
| ridder | R | 必需 | 不限 | 不限 | 保证 | 1.41 ≤ p ≤ 2.0 1.41\leq p\leq2.0 1.41≤p≤2.0 |
| toms748 | R | 必需 | 不限 | 不限 | 保证 | 1.65 ≤ p ≤ 2.7 1.65\leq p\leq2.7 1.65≤p≤2.7 |
| secant | R/C | 需近似解x0,x1 | 无需 | 无需 | 不保证 | 1.62 |
| newton | R/C | 需近似解x0 | 必需 | 无需 | 不保证 | 1.41 ≤ p ≤ 2.0 1.41\leq p\leq2.0 1.41≤p≤2.0 |
| halley | R/C | 需近似解x0 | 必需 | 必需 | 不保证 | 1.44 ≤ p ≤ 3.0 1.44\leq p\leq3.0 1.44≤p≤3.0 |
method参数的缺省值是系统按所提供的参数使用适用于所呈现情况的最佳方法。如果提供了包含根的区间,它可能会使用区间方法之一(bisect、brentq、brenth、rider、toms748)。如果指定了导数和初始值,它可以选择基于导数的方法之一(secant、newton、halley)。如果没有方法被判定为适用,它将引发异常。
例2:计算函数
f
(
x
)
=
1
+
(
2
−
x
)
2
1
+
x
2
f(x)=\frac{1+(2-x)^2}{1+x^2}
f(x)=1+x21+(2−x)2的最大值点
x
0
x_0
x0。
解:由于
f
(
x
)
f(x)
f(x)二阶连续可微,为计算
f
(
x
)
f(x)
f(x)的最大值点,先求得
f
(
x
)
f(x)
f(x)驻点。令
f
′
(
x
)
=
4
(
(
x
−
1
)
2
−
2
)
(
1
+
x
2
)
2
=
0
f'(x)=\frac{4((x-1)^2-2)}{(1+x^2)^2}=0
f′(x)=(1+x2)24((x−1)2−2)=0
解此方程,得驻点。按二阶可微函数极值点的必要条件,计算
f
(
x
)
f(x)
f(x)的二阶导数
f
′
′
(
x
)
f''(x)
f′′(x)在驻点处的值,通过二阶导数值的正负以判断是极大值点或是极小值点。下列代码完成计算过程。
from scipy.optimize import root_scalar #导入root_scalar
answer={True:'极小点',False:'极大点'} #设置驻点标签字典
f=lambda x: (1+(2-x)**2)/(1+x**2) #设置目标函数
f1=lambda x:4*((x-1)**2-2)/(1+x**2)**2 #设置导函数
x0=root_scalar(f1,bracket=(-2,0)).root #计算区间(-2,0)内驻点
_,f2=der_scalar(f,x0) #计算驻点处二阶导数
print('x0=%.4f为%s,f(x0)=%.4f'%(x0,answer[f2>0],f(x0))) #驻点标签
x0=root_scalar(f1,bracket=(2,3)).root #计算区间(2,3)内驻点
_,f2=der_scalar(f,x0) #计算驻点处二阶导数
print('x0=%.4f为%s,f(x0)=%.4f'%(x0,answer[f2>0],f(x0))) #驻点标签
程序的第2行设置驻点的极值属性标签字典answer:True对应“极小点”,False对应“极大点。第3、4行分别设置目标函数表达式f及其1阶导函数f1。第5行调用root_scalar(第1行导入),传递区间(-2,0)给参数bracket,method参数使用缺省值自动求解方程 f ′ ( x ) = 0 f'(x)=0 f′(x)=0赋予x0。第6行调用der_scalar函数(详见博文《最优化方法Python计算:一元函数导数的数值计算》),计算 f ( x ) f(x) f(x)在驻点x0处的二阶导数赋予f2,第7行以f2是否大于零而确定x0的极值点属性。相仿地,第8~10行计算 f ( x ) f(x) f(x)在区间 ( 2 , 3 ) (2,3) (2,3)内的驻点,并确定其极值点属性。运行程序,输出文章来源:https://www.toymoban.com/news/detail-645399.html
x0=-0.4142为极大点,f(x0)=5.8284
x0=2.4142为极小点,f(x0)=0.1716
这意味着驻点-0.4142,极大值为5.8284。驻点2.4142是函数 f ( x ) f(x) f(x)的极小值点,极小值为0.1716。所以,最大值点为-0.4142。文章来源地址https://www.toymoban.com/news/detail-645399.html
到了这里,关于最优化方法Python计算:解一元方程的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!