【二分图】 二分图上匹配问题 和 匈牙利算法正确性说明
-
本文讨论无权图
-
思维上没什么难度,但是文字量却比自己想的要多……
0. 一些前置
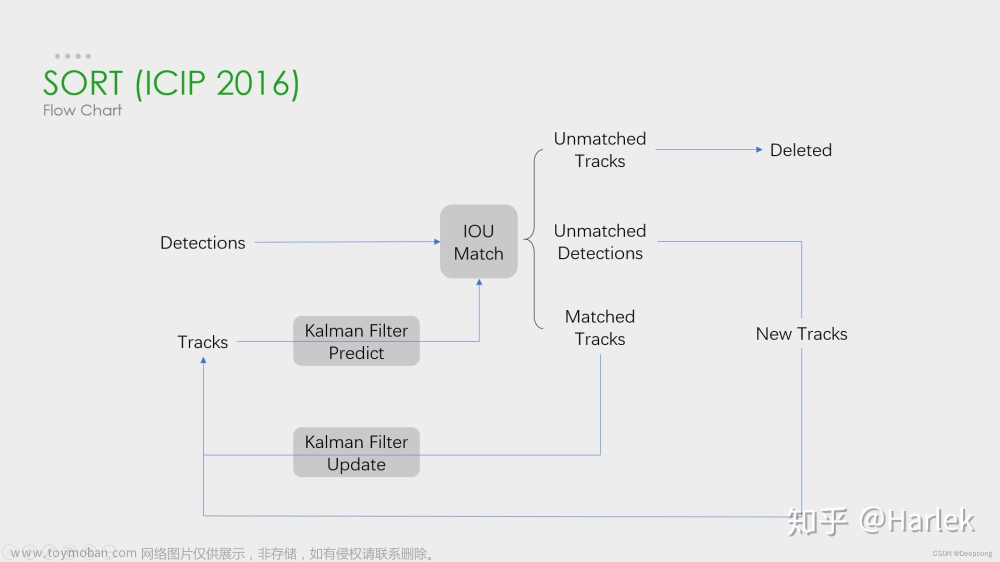
- 什么是二分图上的匹配?什么是匈牙利算法?
“二分图最大匹配概念、匈牙利算法” 这里引用 Pecco 的介绍。这篇文章写的非常通俗易懂,而且揭示了匈牙利算法(或者说增广路)的本质是“朴素的匹配调整”。
- 增广路、交错路是什么?
“增广路、交错路概念” 这里引用 OI-wiki 的内容介绍。
1.匈牙利算法跑完之后,二分图中不存在增广路
我们先强调一下,在二分图上增广路的一些性质。因为增广路一定有偶数个点、奇数条边,因此二分图上增广路的两个端点一定分别在两侧。那么显然,如果从一侧出发找不到增广路,那么从另一侧出发肯定也找不到。以及增广路中除了两端点外所有的点都是匹配点,以及增广路中最左右两条边是未匹配的,剩下的边交替着匹配和未匹配。
因此,只要证明了从一侧的任一点出发都找不到增广路,那么整张二分图就没有增广路。我们不妨假设从左侧出发。
我们归纳地证明一下(通过讨论匈牙利算法进行到左侧的第几个点)。我们要证明的是,匈牙利算法进行完某一个点之后,从这个点出发以及从之前的(左侧的)点出发都找不到增广路,即图中没有增广路。下文的提及的“前xx个点“都是数左侧的点。
首先,当一开始算法进行完 \(0\) 个点的时候,前 \(0\) 个点中没有增广路。如果你不放心,那么我们考虑算法进行第一个点,要么有增广路被增广了 第一个点变成了匹配点 ,从前 \(1\) 个点出发没有增广路;要么就找不到增广路,同样从前 \(1\) 个点出发没有增广路。
现在我们假设前 \(k\) 个点出发没有增广路,我们想证明,在进行完第 \(k + 1\) 个点的搜索、(可能存在的)增广之后,图中不存在增广路。
如果从这个点出发找不到增广路,那么也肯定不会有任何操作,也就不会影响前面的点的结果,因此前 \(k + 1\) 个点中没有增广路。
如果从新加入的这个点出发找到了增广路,那么这条路就要被增广,增广之后就不是增广路了。我们现在唯一要考虑的就是,这条路增广的过程中,会不会影响先前的点,使得先前的点中间出现增广路?
增广完成后,增广的路径上都变成了匹配点。
我们考虑增广完成后的情况。假设,增广完成后,在之前的点中间(只能在之前的点中间出现在增广路,因为新点已经被匹配了),出现了增广路。
(本图中内容涵盖上文和下文,请结合对应部分内容阅读)

加入新的增广路 和 这次被增广的增广路没有交点,那就矛盾了,因为这次增广过程根本不会影响到这条路径,那么这条所谓的“新的”增广路在之前就是增广路,不符合我们的假设。
两条路径相交的时候,一条是我们发现的新的增广路,一条是本轮中经过增广后,整个路径上全部被匹配的路径。那么显然相交点不可能存在于增广路的两端,因为另一条路上的点全匹配了,增广路上没匹配。
(接下来的说明中,涉及到奇偶性的证明和匹配、未匹配冲突的说明,见上图)
我们考虑相交在增广路中间的时候,如果只是点相交但没有边的重合,那么显然是矛盾的,因为这样会产生匹配冲突。
如果有边的重合,那么我们还原到本轮增广之前的情况,肯定可以选取“新增广路”的端点和之前的端点形成增广路,与之前不存在增广路矛盾(画一下就可以知道)。
因此可以证明,本轮增广不会使得之前的点中形成新的增广路,整个图中没有增广路。这种情况也成立。
因此归纳成立。匈牙利算法进行完成后,二分图中不存在增广路。
2. 二分图中不存在增广路 等价于 达到最大匹配
我们把原命题逆否一下(逆否之后肯等等价),二分图没达到最大匹配 等价于 二分图中存在增广路
后推前是明显成立的。因为二分图中如果有增广路,那肯定可以增广一下,匹配数量+1。
前推后在这里引用一个证明:“匈牙利算法匹配即最大匹配的证明” 这里面的证明基于“匈牙利算法跑完后、二分图中不存在增广路”,也就是之前的证明。
3.最大匹配数 等于 最小点覆盖数
“二分图最大匹配的König定理及其证明” 在这里我引用了 Matrix67 的证明。下文关于König定理的证明是参考的这篇文章。
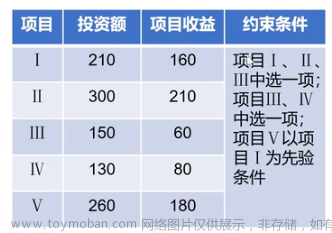
简而言之,最小点覆盖数的“瓶颈”是有多少条不相交的边(因为都得盖上)。所以最小覆盖数 \(\ge\) 最大匹配数(就是最多的不相交的边)。而当达成最大匹配之后,二分图中的匹配边可以分“方向”(和未匹配点的连接方式有关),按照方向在匹配边两个端点中的一个选择覆盖。最终证明可以覆盖所有边。那么最小点覆盖数 \(=\) 最大匹配数。
4.题外话:非二分图上的无权图的匹配
思路:在图上进行 BFS 或者 DFS 进行染色,转化为二分图。那么有:如果存在奇环,那么不能直接转化成二分图,否则是可以的。涉及到奇环的问题需要缩点等技巧,就另见“带花树算法”了。
首先,二分图只可能有偶环,没有奇环。我们假设二分图形成了环状结构,那么存在一条路径以某一点为起点和终点。根据二分图性质,因为起点和终点同一个点,所以一定处于同一侧,那么路径长度就一定为偶数,因此只能有偶环,不能有奇环。
其次,我们考虑对一个无向图进行 dfs 染色,黑白相间。我们考虑搜索树上的情况,因为无向图 dfs 树只有 T 边和 B 边,T边上显然不冲突。考虑 B 边构成环的情况。可以看出,如果颜色染色不冲突,那么根据奇偶性质,一定是偶环,偶环不冲突。奇环一定冲突,所以不可能是奇环。文章来源:https://www.toymoban.com/news/detail-647126.html
于是,有点充要的,二分图和不含奇环的无向图可以相互转化。至于唯一性,那需要考虑连通性的问题了。文章来源地址https://www.toymoban.com/news/detail-647126.html
到了这里,关于【二分图】 二分图上匹配问题 和 匈牙利算法正确性说明的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!