1. Toy模板网首页
  2. > Toy博客

矩阵乘法的三种算法(蛮力嵌套循环法，分治递归法，Strassen法)

9月前 作者：GodFishhh 分类：Toy博客 阅读(32) 违法举报

这篇具有很好参考价值的文章主要介绍了矩阵乘法的三种算法(蛮力嵌套循环法，分治递归法，Strassen法)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

一.矩阵乘法的嵌套循环算法

二.矩阵乘法的递归算法

三.矩阵乘法的Strassen算法

一.矩阵乘法的嵌套循环算法

伪代码：

矩阵乘法算法,算法导论,算法,算法

C++代码：

//1.矩阵乘法的嵌套循环算法
#include<iostream>
using namespace std;

void Square_MA_MU(int a[][3],int b[][3],int c[][3],int n) //传递二维数组参数时必须要确定列数
{
	for (int i = 0; i < n; i++)  //行遍历
	{
		for(int j=0;j<n;j++) //列遍历
		{
			for (int x = 0; x < n; x++)
			{
				c[i][j] += a[x][i] * b[j][x]; //一行一行的元素计算
			}
		}
	}
}

int main()
{
	int a1[3][3]
	{
		1,1,1,
		2,2,2,
		3,3,3
	};
	int b1[3][3]
	{
		2,2,2,
		1,1,1,
		3,3,3
	};
	int c1[3][3] =
	{
		0,0,0,
		0,0,0,
		0,0,0
	};//进行初始化
	cout << "矩阵相乘前的c1： " << endl;
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			cout << c1[i][j] << " ";
		}
		cout << endl;
	}
	Square_MA_MU(a1, b1, c1, 3);
	cout << "a1*b1得到的c1：" << endl;
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			cout << c1[i][j]<<" ";
		}
		cout << endl;
	}

	system("pause");
	return 0;
}

二.矩阵乘法的递归算法

伪代码：

矩阵乘法算法,算法导论,算法,算法

C++代码：

#include<iostream>
using namespace std;

void matrix_multi_recursive(int a[][8], int m, int n, int b[][8], int p, int q, int size, int c[][8]) //m,n是矩阵a的位置参数，p,q是矩阵b
{
	if (size == 1)
	{
		c[m][q] += a[m][n] * b[p][q];
	}
	else
	{
		int half_size = size / 2;
		//分块进行递归运算，分块的基本原则为 half_size 即为 size/2 
		//初始状态下共分八块，再依次递归求得矩阵相乘的结果
		matrix_multi_recursive(a, m, n, b, p, q, half_size, c);
		matrix_multi_recursive(a, m, n + half_size, b, p + half_size, q, half_size, c);
		matrix_multi_recursive(a, m, n, b, p, q + half_size, half_size, c);
		matrix_multi_recursive(a, m, n + half_size, b, p + half_size, q + half_size, half_size, c);
		matrix_multi_recursive(a, m + half_size, n, b, p, q, half_size, c);
		matrix_multi_recursive(a, m + half_size, n + half_size, b, p + half_size, q, half_size, c);
		matrix_multi_recursive(a, m + half_size, n, b, p, q + half_size, half_size, c);
		matrix_multi_recursive(a, m + half_size, n + half_size, b, p + half_size, q + half_size, half_size, c);
	}
}

void print(int c[][8], int size)
{
	int i, j;
	for (i = 0; i < size; i++)
	{
		for (j = 0; j < size; j++)
		{
			cout << c[i][j] << " ";
		}
		cout << endl;
	}
}



int main()
{
	int a[8][8] = 
	{ 
	{1,2,3,4,5,6,7,8},
	{2,3,4,5,6,7,8,9},
	{3,4,5,6,7,8,9,10},
	{4,5,6,7,8,9,10,11},
	{5,6,7,8,9,10,11,12},
	{6,7,8,9,10,11,12,13},
	{7,8,9,10,11,12,13,14},
	{8,9,10,11,12,13,14,15}
	};

	int b[8][8] =
	{
	{10,11,12,13,14,15,16,17},
	{11,12,13,14,15,16,17,18},
	{12,13,14,15,16,17,18,19},
	{13,14,15,16,17,18,19,20},
	{14,15,16,17,18,19,20,21},
	{15,16,17,18,19,20,21,22},
    {16,17,18,19,20,21,22,23},
	{17,18,19,20,21,22,23,24}
	};
	int c[8][8];
	for (int i = 0; i < 8; i++)
	{
		for (int j = 0; j < 8; j++)
		{
			c[i][j] = 0;
		}
	}
	matrix_multi_recursive(a, 0, 0, b, 0, 0, 8, c);
	print(c, 8);
	return 0;
	system("pause");
	return 0;
}

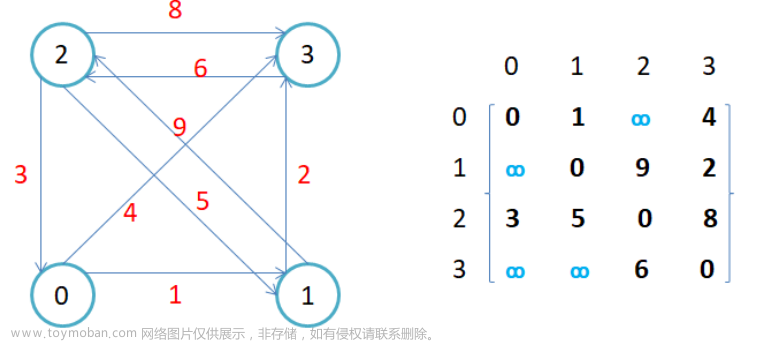
原理：矩阵乘法的分块运算：

【2.5】矩阵分块相乘 - 知乎 (zhihu.com)

复杂度：

矩阵乘法算法,算法导论,算法,算法

三.矩阵乘法的Strassen算法

伪代码：

矩阵乘法算法,算法导论,算法,算法

C++代码：

#include "stdafx.h"
#include <stdio.h>
#include <iostream>
#include <windows.h>
#include <ctime>
using namespace std;
 
 
template <typename T>
class Strassen
{
public:
	void ADD(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size);
	void SUB(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size);
	void NormalMul(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size);
	void StrassenMul(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size);
	void FillMatrix(T **  MatrixA, T ** MatrixB, int size);//给A、B矩阵赋初值
	int   GetMatrixSum(T ** Matrix, int size);
	//用来计算矩阵各个元素的和，如果两种算法得出的矩阵的和相等则认为算法正确。
};
 
template <typename T>
void Strassen<T>::ADD(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size)
{
	for(int i = 0; i < size; i++)
	{
		for(int j = 0; j < size; j++)
		{
			MatrixResult[i][j] = MatrixA[i][j] + MatrixB[i][j];
		}
	}
}
 
template <typename T>
void Strassen<T>::SUB(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size)
{
	for(int i = 0; i < size; i++)
	{
		for(int j = 0; j < size; j++)
		{
			MatrixResult[i][j] = MatrixA[i][j] - MatrixB[i][j];
		}
	}
}

template <typename T>
void Strassen<T>::NormalMul(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size)
{
	for(int i = 0; i < size; i++)
	{
		for(int j = 0; j < size; j++)
		{
			MatrixResult[i][j] = 0;
			for(int k = 0; k < size; k++)
				MatrixResult[i][j] += MatrixA[i][k] * MatrixB[k][j];
		}
	}
}
 
template <typename T>
void Strassen<T>::FillMatrix(T **  MatrixA, T ** MatrixB, int size)//给A、B矩阵赋初值
{
	for(int i = 0; i < size; i++)
	{
		for(int j = 0; j < size; j++)
		{
			MatrixA[i][j] = MatrixB[i][j] = rand() % 5; 
		}
	}	
}
 
template <typename T>
void Strassen<T>::StrassenMul(T **  MatrixA, T ** MatrixB, T ** MatrixResult, int size)
{
	// if ( size <= 64 )    
	//分治门槛，小于这个值时不再进行递归计算，而是采用常规矩阵计算方法
	// {
	// 	NormalMul(MatrixA, MatrixB, MatrixResult, size);
	// }
	if(size == 1)
	{
		MatrixResult[0][0] = MatrixA[0][0] * MatrixB[0][0];
	}
	else
	{
		int half_size = size / 2;
		T ** A11; T ** A12; T ** A21; T ** A22;
		T ** B11; T ** B12; T ** B21; T ** B22;
		T ** C11; T ** C12; T ** C21; T** C22;
		T ** M1; T ** M2; T ** M3; T ** M4; T ** M5; T ** M6; T ** M7;
		T ** MatrixTemp1; T ** MatrixTemp2;
 
		A11 = new int * [half_size];
		A12 = new int * [half_size];
		A21 = new int * [half_size];
		A22 = new int * [half_size];
 
		B11 = new int * [half_size];
		B12 = new int * [half_size];
		B21 = new int * [half_size];
		B22 = new int * [half_size];
 
		C11 = new int * [half_size];
		C12 = new int * [half_size];
		C21 = new int * [half_size];
		C22 = new int * [half_size];
 
		M1 = new int * [half_size];
		M2 = new int * [half_size];
		M3 = new int * [half_size];
		M4 = new int * [half_size];
		M5 = new int * [half_size];
		M6 = new int * [half_size];
		M7 = new int * [half_size];
		MatrixTemp1 = new int * [half_size];
		MatrixTemp2 = new int * [half_size];
 
		for(int i = 0; i < half_size; i++)
		{
			A11[i] = new int[half_size];	
			A12[i] = new int[half_size];	
			A21[i] = new int[half_size];	
			A22[i] = new int[half_size];
			
			B11[i] = new int[half_size];	
			B12[i] = new int[half_size];	
			B21[i] = new int[half_size];	
			B22[i] = new int[half_size];
			
			C11[i] = new int[half_size];	
			C12[i] = new int[half_size];	
			C21[i] = new int[half_size];	
			C22[i] = new int[half_size];
 
			M1[i] = new int[half_size];	
			M2[i] = new int[half_size];	
			M3[i] = new int[half_size];	
			M4[i] = new int[half_size];
			M5[i] = new int[half_size];	
			M6[i] = new int[half_size];	
			M7[i] = new int[half_size];
 
			MatrixTemp1[i] = new int[half_size];	
			MatrixTemp2[i] = new int[half_size];
		}
 
		//赋值
		for(int i = 0; i < half_size; i++)
		{
			for(int j = 0; j < half_size; j++)
			{
				A11[i][j] = MatrixA[i][j];
				A12[i][j] = MatrixA[i][j+half_size];
				A21[i][j] = MatrixA[i+half_size][j];
				A22[i][j] = MatrixA[i+half_size][j+half_size];
 
				B11[i][j] = MatrixB[i][j];
				B12[i][j] = MatrixB[i][j+half_size];
				B21[i][j] = MatrixB[i+half_size][j];
				B22[i][j] = MatrixB[i+half_size][j+half_size];
			}
		}		
 
		//calculate M1
		ADD(A11, A22, MatrixTemp1, half_size);
		ADD(B11, B22, MatrixTemp2, half_size);
		StrassenMul(MatrixTemp1, MatrixTemp2, M1,half_size);
 
		//calculate M2
		ADD(A21, A22, MatrixTemp1, half_size);
		StrassenMul(MatrixTemp1, B11, M2, half_size);
 
		//calculate M3
		SUB(B12, B22, MatrixTemp1, half_size);
		StrassenMul(A11, MatrixTemp1, M3, half_size);
 
 
		//calculate M4
		SUB(B21, B11, MatrixTemp1, half_size);
		StrassenMul(A22, MatrixTemp1, M4, half_size);
 
		//calculate M5
		ADD(A11, A12, MatrixTemp1, half_size);
		StrassenMul(MatrixTemp1, B22, M5, half_size);
 
		//calculate M6
		SUB(A21, A11, MatrixTemp1, half_size);
		ADD(B11, B12, MatrixTemp2, half_size);
		StrassenMul(MatrixTemp1, MatrixTemp2, M6, half_size);
 
		//calculate M7
		SUB(A12, A22, MatrixTemp1, half_size);
		ADD(B21, B22, MatrixTemp2, half_size);
		StrassenMul(MatrixTemp1, MatrixTemp2, M7, half_size);
 
		//C11
		ADD(M1, M4, C11, half_size);
		SUB(C11, M5, C11, half_size);
		ADD(C11, M7, C11, half_size);
 
		//C12
		ADD(M3, M5, C12, half_size);
 
		//C21
		ADD(M2, M4, C21, half_size);
 
		//C22
		SUB(M1, M2, C22, half_size);
		ADD(C22, M3, C22, half_size);
		ADD(C22, M6, C22, half_size);
 
		//赋值
		for(int i = 0; i < half_size; i++)
		{
			for(int j = 0; j < half_size; j++)
			{
				MatrixResult[i][j] = C11[i][j];
				MatrixResult[i][j+half_size] = C12[i][j];
				MatrixResult[i+half_size][j] = C21[i][j];
				MatrixResult[i+half_size][j+half_size] = C22[i][j];
			}
		}
 
		//释放申请的内存
		for(int i = 0; i < half_size; i++)
		{
			delete[] A11[i];	
			delete[] A12[i];	
			delete[] A21[i];	
			delete[] A22[i];
			
			delete[] B11[i];	
			delete[] B12[i];	
			delete[] B21[i];	
			delete[] B22[i];
			
			delete[] C11[i];	
			delete[] C12[i];	
			delete[] C21[i];	
			delete[] C22[i];
 
			delete[] M1[i];	
			delete[] M2[i];	
			delete[] M3[i];	
			delete[] M4[i];	
			delete[] M5[i];	
			delete[] M6[i];	
			delete[] M7[i];
			
			delete[] MatrixTemp1[i];	
			delete[] MatrixTemp2[i];
		}
		delete[] A11;	
		delete[] A12;	
		delete[] A21;	
		delete[] A22;
		
		delete[] B11;	
		delete[] B12;	
		delete[] B21;	
		delete[] B22;
		
		delete[] C11;	
		delete[] C12;	
		delete[] C21;	
		delete[] C22;
 
		delete[] M1;	
		delete[] M2;	
		delete[] M3;	
		delete[] M4;	
		delete[] M5;	
		delete[] M6;	
		delete[] M7;
		
		delete[] MatrixTemp1;	
		delete[] MatrixTemp2;
	}
}
 
template <typename T>
int   Strassen<T>::GetMatrixSum(T ** Matrix, int size)
{
	int sum = 0;
	for(int i = 0; i < size; i++)
	{
		for(int j = 0; j < size; j++)
		{
			sum += Matrix[i][j];
		}
	}	
	return sum;
}
 
int main()
{
	long startTime_normal, endTime_normal;
	long startTime_strasse, endTime_strassen;
 
	//srand(time(0));
 
	Strassen<int> stra;
	int N;
	cout<<"please input the size of Matrix,and the size must be the power of 2:"<<endl;
	cin>>N;
 
	int ** Matrix1 = new int * [N];
	int ** Matrix2 = new int * [N];
	int ** Matrix3 = new int * [N];
	for(int i=0;i<N;i++)
	{
		Matrix1[i] = new int[N];
		Matrix2[i] = new int[N];
		Matrix3[i] = new int[N];
	}
 
	stra.FillMatrix(Matrix1, Matrix2,N);
 
	cout << "朴素算法开始时间：" << (startTime_normal = clock()) << endl;
	stra.NormalMul(Matrix1, Matrix2, Matrix3,N);
	cout << "朴素算法结束时间：" << (endTime_normal = clock()) << endl;
	cout << "总时间:" << endTime_normal-startTime_normal << endl;
	cout << "sum = " << stra.GetMatrixSum(Matrix3,N) << ';' << endl;
 
	cout << "Strassen算法开始时间：" << (startTime_strasse= clock()) << endl;
	stra.StrassenMul(Matrix1,Matrix2,Matrix3,N);
	cout << "Strassen算法结束时间：" << (endTime_strassen = clock()) << endl;
	cout << "总时间:" << endTime_strassen-startTime_strasse << endl;
	cout << "sum = " << stra.GetMatrixSum(Matrix3,N) << ';' << endl;
}

核心思想：令递归树不那么茂盛一点，即只进行七次递归而不是八次。

复杂度：

矩阵乘法算法,算法导论,算法,算法文章来源地址https://www.toymoban.com/news/detail-649370.html

到了这里，关于矩阵乘法的三种算法(蛮力嵌套循环法，分治递归法，Strassen法)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • Java嵌套循环的使用与九九乘法表的输出

    嵌套循环：将一个循环结构A声明在另一个循环结构B的循环体中，就构成了嵌套循环         外层循环：循环结构B         内层循环：循环结构A 说明         ①内层循环结构遍历一遍，只相当于外层循环循环体执行了一次         ②假设外层循环需要执行m次

    2023年04月18日
    浏览(45)
  • Python---练习：使用for循环嵌套实现打印九九乘法表

    Python---练习：使用for循环嵌套实现打印九九乘法表

    思考： 外层 循环主要用于控制循环的 行数 ， 内层 循环用于控制 列数。 基本语法： 序列1  序列2 ，就可以是range(1, 10)   -----也就是从1，到9。 参考while循环： 相关链接Python---练习：使用while嵌套循环打印 9 x 9乘法表-CSDN博客 最终代码：

    2024年02月08日
    浏览(38)
  • 【数据结构】稀疏矩阵存储的三种方法及三元组表示稀疏矩阵转置算法的两种实现 —— C++

    【数据结构】稀疏矩阵存储的三种方法及三元组表示稀疏矩阵转置算法的两种实现 —— C++

    1. 三元组顺序表数据结构 注意：data[]中的元素是按行存储或者按列存储的，所以 在将三元组逆置时，不能简单地将行列下标对换，data[]数组中元素的顺序也需要重新排列 2. 三元组表示稀疏矩阵转置算法1 3. 三元组表示稀疏矩阵转置算法2：快速转置 为了 便于随机存取任意一

    2024年02月05日
    浏览(43)

  • Java的三种循环

    1.1 switch语句结构（掌握） 1. 格式： 复制 2. 执行流程： 首先计算出表达式的值 其次，和case依次比较，一旦有对应的值，就会执行相应的语句，在执行的过程中，遇到break就会结束。 最后，如果所有的case都和表达式的值不匹配，就会执行default语句体部分，然后程序结束掉。

    2024年02月21日
    浏览(33)

  • java跳出for循环的三种常见方法

    这篇文章主要给大家介绍了关于java跳出for循环的三种常见方法,需要的朋友可以参考下 一、 break语句：使用break语句可以结束整个for循环的执行： 当 i 等于5时， break 语句会将控制流程跳出 for 循环从而停止后续代码的执行。 二、 return语句：如果你想要跳出当前方法并且停止

    2024年04月23日
    浏览(35)
  • Python中退出While循环的三种方法举例

    Python中退出While循环的三种方法举例

    在Python学习及编程应用中，常会使用while循环，对while循环条件设置不当可能导致进入死循环，本文将举例说明三种退出while循环的方法。 利用input函数使得输入值传递到while之后的条件判断句中，使while后的结果为False。 举例： 程序1： 运行结果举例 使用input将输入的值，通过

    2024年02月09日
    浏览(42)

  • 生产项目中基于springboot项目解决循环依赖的三种方式

    在生产项目中，可以使用Spring Boot框架来快速开发Spring应用程序。Spring Boot提供了一种方便的方式来创建独立的，基于Spring的应用程序，并且有着高度的自动化配置和开箱即用的特性。 可以使用@Lazy注解来控制Bean的延迟初始化，同时可以使用AOP切面编程来解决循环依赖问题。

    2024年02月11日
    浏览(51)

  • 1.矩阵的三种不变因子

    本文主要介绍多项式矩阵的基本概念和等价，用于为相似标准型进行铺垫 此处将由数组成的矩阵拓展为以多项式为元的矩阵，即多项式矩阵 【定义】多项式矩阵的秩 设 A ( λ ) ∈ F [ λ ] m × n ， A ( λ ) ≠ 0 A(lambda)in F[lambda]^{mtimes n}，A(lambda)neq0 A ( λ ) ∈ F [ λ ] m × n ， A

    2024年01月20日
    浏览(38)
  • 蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题

    蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题

    这两种搜索方法本质上都是基于蛮力法思路 这两种搜索方法对有向图和无向图都适用 1.1 邻接矩阵 邻接矩阵示意图： 1.2 邻接表 注意：边结点代表的是图中的边，而并非图中的结点；头结点才表示图中的结点；头结点身后所连接的为边结点 邻接表示意图：（一般默认为出边

    2024年02月05日
    浏览(65)
  • 矩阵算法之矩阵乘法

    矩阵算法之矩阵乘法

    矩阵算法在图像处理、神经网络、模式识别等领域有着广泛的用途。 在矩阵乘法中，A矩阵和B矩阵可以做乘法运算必须满足A矩阵的列的数量等于B矩阵的行的数量。 运算规则：A的每一行中的数字对应乘以B的每一列的数字把结果相加起来。 1、当矩阵A的列数（column）等于矩阵

    2024年02月11日
    浏览(38)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包