Scalable Diffusion Models with Transformers

Scalable Diffusion Models with Transformers

论文地址：
https://arxiv.org/pdf/2212.09748.pdf

项目地址：
https://github.com/facebookresearch/DiT

论文主页：
https://www.wpeebles.com/DiT

摘要

我们探索了一类新的基于Transformer结构的扩散模型。我们训练图像的潜在扩散模型，用一个对潜在补丁操作的Transformer取代常用的U-Net骨干网。我们通过Gflops测量的前向传递复杂性来分析扩散Transformer(dit)的可伸缩性。我们发现，具有较高gflop的dit(通过增加Transformer深度/宽度或增加输入令牌数量)始终具有较低的FID。除了具有良好的可扩展性属性外，我们最大的DiT-XL/2模型在类条件ImageNet 512×512和256×256基准上优于所有先前的扩散模型，在后者上实现了2.27的最先进的FID

1. 介绍

在Transformer的推动下，机器学习正在经历复兴。在过去的五年中，用于自然语言处理[8,39]、视觉[10]和其他几个领域的神经架构在很大程度上已经被Transformer[57]所包含。许多图像级生成模型仍然不受这一趋势的影响，尽管Transformer在自回归模型中得到了广泛的应用[3,6,40,44]，但它们在其他生成建模框架中应用较少。例如，扩散模型一直处于图像级生成模型最新进展的前沿[9,43];然而，它们都采用卷积U-Net架构作为骨干网的事实上选择。

Ho等人的开创性工作[19]首次为扩散模型引入了U-Net骨干网。设计选择继承自pixelcnn++[49,55]，一个自回归生成模型，有一些架构上的变化。该模型是卷积的，主要由ResNet[15]块组成。与标准U-Net[46]相比，附加的空间自注意块是Transformer中的基本组件，以较低的分辨率散布。Dhariwal和Nichol[9]消除了U-Net的几种架构选择，例如使用自适应归一化层[37]为卷积层注入条件信息和通道计数。然而，Ho等人的U-Net的高级设计在很大程度上保持完整。

通过这项工作，我们的目标是揭开扩散模型中建筑选择的意义，并为未来的生成建模研究提供经验基线。我们表明，U-Net电感偏差对扩散模型的性能不是至关重要的，并且它们可以很容易地用标准设计(如Transformer)取代。因此，扩散模型很好地准备从架构统一的最近趋势中获益。通过继承其他领域的最佳实践和培训方法，以及保留可伸缩性、健壮性和效率等有利属性。标准化的体系结构也将为跨领域研究开辟新的可能性。

本文讨论了一类新的基于Transformer的扩散模型。我们称之为扩散Transformer，简称dit。dit坚持视觉Transformer(ViTs)[10]的最佳实践，它已被证明比传统的卷积网络(例如ResNet[15])更有效地扩展视觉识别。

更具体地说，我们研究了Transformer的标度行为与网络复杂度和样本质量的关系。我们表明，通过在潜伏扩散模型(ldm)[45]框架下构建和对标DiT设计空间，其中扩散模型在V AE的潜伏空间内训练，我们可以成功地用Transformer取代U-Net骨干。我们进一步表明dit是扩散模型的可扩展架构:网络复杂性(由Gflops测量)与样本质量(由FID测量)之间存在很强的相关性。通过简单地扩展DiT并训练具有高容量主干(118.6 Gflops)的LDM，我们能够在256 × 256类条件ImageNet生成基准上实现2.27 FID的最先进结果。

2. 相关工作

Transformer。Transformer[57]已经取代了跨语言、视觉[10]、强化学习[5,23]和元学习[36]的特定领域架构。它们在增加模型大小、训练语言域[24]的计算和数据时表现出了显著的缩放特性，如通用自回归模型[17]和ViTs[60]。除了语言，Transformer已经被训练为自回归预测像素[6,7,35]。它们还在离散码本[56]上进行了训练，作为自回归模型[11,44]和掩模生成模型[4,14];前者在20B参数[59]下表现出优异的缩放性能。最后，在DDPMs中探索了Transformer对非空间数据的综合;例如，在DALL·E 2中生成CLIP图像嵌入[38,43]。本文研究了Transformer作为图像扩散模型主干时的标度特性。

去噪扩散概率模型(DDPM)。扩散[19,51]和基于分数的生成模型[22,53]作为图像的生成模型特别成功[32,43,45,47]，在许多情况下优于以前最先进的生成对抗网络(GANs)[12]。过去两年DDPM的改进主要是由改进的采样技术驱动的[19,25,52]，最显著的是无分类引导[21]，重新定义扩散模型以预测噪声而不是像素[19]，并使用级联DDPM管道，其中低分辨率基础扩散模型与上采样器并行训练[9,20]。对于上面列出的所有扩散模型，卷积U-Nets[46]实际上是骨干架构的选择。

体系结构的复杂性。在图像生成文献中评估体系结构复杂性时，使用参数计数是相当常见的实践。一般来说，参数计数不能很好地代表图像模型的复杂性，因为它们不能说明图像分辨率等显著影响性能的因素[41,42]。相反，本文中的大部分模型复杂性分析都是通过理论Gflops的透镜进行的。这使我们与架构设计文献保持一致，在这些文献中，gflop被广泛用于衡量复杂性。在实践中，黄金复杂度度量仍然存在争议，因为它经常依赖于特定的应用场景。Nichol和Dhariwal改进扩散模型的开创性工作[9,33]与我们最相关，在那里，他们分析了U-Net架构类的可伸缩性和Gflop属性。在本文中，我们主要关注transformer类。

3. Diffusion Transformers

3.1. Preliminaries

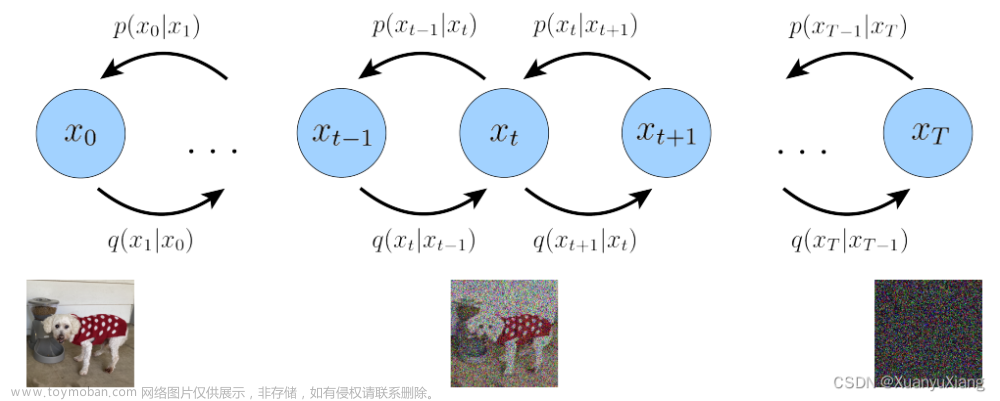
扩散公式。在介绍我们的体系结构之前，我们简要回顾了理解扩散模型(DDPM)所需的一些基本概念[19,51]。高斯扩散模型假设一个前向噪声处理过程，逐步将噪声应用于真实数据$x_0:q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)=N\left({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right)$

其中常量${\bar{\alpha }}_t$是超参数。通过应用重新参数化技巧，我们可以对${\mathrm{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathrm{x}}_0+\sqrt{1-\overline{{\alpha }_l}}ϵ$，其中${\epsilon}{\in} {\mathcal{N}(0,I)} $。

扩散模型被训练来学习反转正向过程破坏的反向过程：$p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};{\mu }_{\theta }\left({\mathbf{x}}_t,t\right),{\Sigma }_{\theta }\left({\mathbf{x}}_t,t\right)\right)$，其中神经网络用于预测$p_{\theta }$的统计量。用$x_0$的对数似然的变分下界[27]来训练逆向过程模型，可简化为：$\mathcal{L}(\theta )=-p(x_0|x_1)+{\sum }_t{\mathrm{D}}_{\mathrm{K}}\mathrm{L}\left(q^{\ast }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,\mathbf{\eta }\right)\Vert p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)\right)$。排除了与训练无关的附加术语。由于$q^{\ast }$和$p_{\theta }$都是高斯分布，$D_{KL}$可以用两个分布的均值和协方差来计算。通过重新参数化${\mu }_{\theta }$作为噪声预测网络${ϵ}_{\theta }$，可以使用预测噪声${ϵ}_{\theta }(x_t)$与地面真理采样高斯噪声${ϵ}_t$之间的简单均方误差来训练模型：$L_{\text{simple }}=E_{t,x_0,ϵ}\left[{\Vert ϵ-{ϵ}_{\theta }\left(x_t,t\right)\Vert }^2\right]$。但是，为了用学习到的反向过程协方差${\Sigma }_{\theta }$训练扩散模型，需要优化完整的$D_{KL}$项。我们遵循Nichol和Dhariwal的方法[33]:用$L_{simple}$训练${ϵ}_{\theta }$，用完整的$L$训练${\Sigma }_{\theta }$。一旦训练$p_{\theta }$，就可以通过初始化$x_{t_{max}}\sim N(0,I)$和通过重新参数化技巧采样$x_{t-1}\sim p_{\theta }(x_{t-1}|x_t)$来对新图像进行采样。

Classifier-free指导。条件扩散模型将额外的信息作为输入，例如类标签c。在这种情况下，相反的过程变成$p_{\theta }(x_{t-1}|x_t,c)$，其中${ϵ}_{\theta }$和${\Sigma }_{\theta }$以$c$为条件。在这种设置下，可以使用无分类器引导来鼓励抽样过程找到x，使$logp(c|x)$高[21]。根据贝叶斯规则，$\log p(c\mid x)\propto \log p(x\mid c)-\log p(x)$，因此${\nabla }_{\sigma }\log p(c\mid x)\propto {\nabla }_{\sigma }\log p(x\mid c)-{\nabla }_{\tau }\log p(x)$。通过将扩散模型的输出解释为得分函数，DDPM抽样程序可以通过以下方法指导$x$到$p(x|c)$高的样本：$p(x\mid c)$ by: ${\widehat{ϵ}}_{\theta }\left(x_t,c\right)={ϵ}_{\theta }\left(x_t,\varnothing \right)+s$. ${\nabla }_x\log p(x\mid c)\propto {ϵ}_{\theta }\left(x_t,\varnothing \right)+s\cdot \left({ϵ}_{\theta }\left(x_t,c\right)-{ϵ}_{\theta }\left(x_t,\varnothing \right)\right)$，其中s > 1为指导尺度(注意s = 1恢复标准抽样)。对c =∅的扩散模型的评估是在训练时随机剔除c，代之以一个习得的“null”嵌入∅。众所周知，与通用抽样技术相比，无分类器指导可以产生显著改善的样本[21,32,43]，而且我们的DiT模型也具有这一趋势。

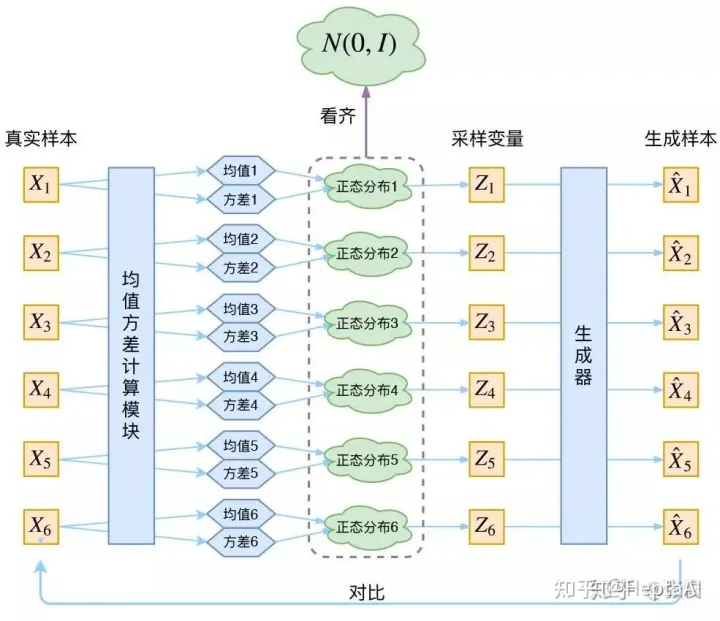
潜在扩散模型。在高分辨率像素空间中直接训练扩散模型在计算上是非常困难的。潜扩散模型(ldm)[45]用两阶段方法解决这个问题:(1)学习一个自编码器，用学习的编码器E将图像压缩成更小的空间表示;(2)训练一个表示$z=E(x)$的扩散模型，而不是图像x (E被冻结)的扩散模型。然后，可以通过从扩散模型中采样表示z来生成新的图像，然后使用学习的解码器$x=D(z)$将其解码为图像。如图2所示，LDM在使用像素空间扩散模型(如ADM)的一小部分gflop的情况下实现了良好的性能。由于我们关心计算效率，这使它们成为架构探索的一个吸引人的起点。在本文中，我们将dit应用于潜在空间，尽管它们也可以应用于像素空间而无需修改。这使得我们的图像生成管道成为一种基于混合的方法；我们使用现成的卷积vav和基于Transformer的DDPM。

3.2. Diffusion Transformer Design Space

我们介绍了扩散Transformer(DiTs)，一种用于扩散模型的新架构。我们的目标是尽可能忠实于标准Transformer架构，以保留其缩放特性。由于我们的重点是训练图像的DDPM(特别是图像的空间表示)，DiT基于视觉转换器(ViT)架构，该架构操作补丁[10]的序列。DiT保留了ViT的许多最佳实践。图3显示了完整DiT体系结构的概述。在本节中，我们将描述DiT的正向传递，以及DiT类的设计空间的组件。

Patchify。DiT的输入是一个空间表示z(对于256 × 256 × 3图像，z的形状为32 × 32 × 4)。DiT的第一层是“patchify”，它通过将每个patch线性嵌入到输入中，将空间输入转换为一个T标记序列，每个标记的维度为d。在patchify之后，我们将标准的基于ViT频率的位置嵌入(sin -cos版本)应用于所有输入令牌。

patchify创建的令牌T的数量由补丁大小超参数p决定。如图4所示，将p减半将使T翻四倍，因此至少使总Transformergflop翻四倍。尽管它对Gflops有重大影响，但请注意，更改p对下游参数计数没有重大影响。

我们将p = 2,4,8添加到DiT设计空间。

DiT块设计。在patchify之后，输入令牌由一系列Transformer块处理。除了有噪声的图像输入外，扩散模型有时还处理附加的条件信息，如噪声时间步长t、类标签c、自然语言等。我们探索了四种不同的Transformer块，它们以不同的方式处理条件输入。该设计对标准ViT块设计进行了微小但重要的修改。各块的设计如图3所示。

​ -情境条件反射。我们简单地将t和c的向量嵌入作为输入序列中的两个附加标记，将它们与图像标记区别对待。这类似于ViT中的cls令牌，它允许我们无需修改就使用标准ViT块。在最后一个块之后，我们从序列中删除条件令牌。这种方法为模型引入了可以忽略不计的新Gflops。

​ -交叉注意模块。我们将t和c的嵌入连接到一个长度为2的序列中，与图像标记序列分开。Transformer块经过修改，在多头自注意块之后增加了一个多头交叉注意层，类似于Vaswani等人的原始设计[57]，也类似于LDM用于类标签的条件调节。交叉注意为模型增加了最多的gflop，大约15%的开销。

​ -Adaptive layer norm (adaLN)块。在GANs中广泛使用自适应归一化层[37][2,26]和使用UNet主干[9]的扩散模型之后，我们探索用自适应层范数(adaLN)取代Transformer块中的标准层范数层。我们不是直接学习量维尺度和移位参数γ和β，而是从t和c的嵌入向量的和中回归它们。在我们探索的三个块设计中，adaLN添加的Gflops最少，因此计算效率最高。它也是唯一限制将相同函数应用于所有令牌的调节机制。

​ -adaln -零块。先前关于ResNets的工作已经发现，将每个剩余块初始化为恒等函数是有益的。例如，Goyal等人发现，在每个块中对最后一批范数尺度因子γ进行零初始化可以加速监督学习设置[13]下的大规模训练。扩散U-Net模型使用类似的初始化策略，在任何剩余连接之前对每个块中的最终卷积层进行零初始化。我们将探索adaLN DiT块的修改，它具有相同的功能。除了回归γ和β，我们还回归在DiT块内任何剩余连接之前立即应用的维度缩放参数α。我们初始化MLP以输出所有α的零向量；这将整个DiT块初始化为恒等函数。与vanilla adaLN块一样，adaLNZero为模型添加了可以忽略不计的gflop。

我们在DiT设计空间中包括上下文内、交叉注意、自适应层规范和adaLN-Zero块。

模型的尺寸。我们应用了N个DiT块序列，每个块的隐藏维度大小为d。在ViT之后，我们使用标准Transformer配置，共同缩放N, d和注意头[10,60]。具体来说，我们使用四种配置:DiT-S, DiT-B, DiT-L和DiT-XL。它们涵盖了广泛的模型大小和触发器分配，从0.3到118.6 gflop，允许我们衡量缩放性能。表1给出了配置的详细信息。我们将B、S、L和XL配置添加到DiT设计空间。

Transformer解码器。在最后一个DiT块之后，我们需要将我们的图像标记序列解码为输出噪声预测和输出对角线协方差预测。这两个输出的形状都等于原始的空间输入。我们使用标准的线性解码器来做到这一点;我们应用最后一层范数(如果使用adaLN则自适应)，并将每个令牌线性解码为p×p×2C张量，其中C是DiT空间输入中的通道数。最后，我们将解码后的标记重新排列到原始的空间布局中，得到预测的噪声和协方差。我们探索的完整DiT设计空间是补丁大小、Transformer块架构和模型大小。

4. 实验设置

我们探索了DiT设计空间，并研究了模型类的缩放属性。我们的模型是根据它们的配置和潜在补丁大小p命名的;例如，DiT-XL/2指的是XLarge配置，p = 2。

训练。我们在ImageNet数据集[28]上训练256 × 256和512 × 512图像分辨率的类条件潜在DiT模型，这是一个高度竞争的生成建模基准。我们用零初始化最后的线性层，否则使用ViT的标准权重初始化技术。我们用AdamW[27,30]训练所有模型。我们使用1 × 10−4的恒定学习速率，没有权重衰减，批处理大小为256。我们使用的唯一数据增强是水平翻转。与之前对vit的许多工作不同[54,58]，我们没有发现学习率热身或正则化对训练dit达到高性能是必要的。即使没有这些技术，训练在所有模型配置中都是高度稳定的，我们没有观察到训练Transformer时常见的任何损失峰值。根据生成建模文献中的常见做法，我们在训练中保持DiT权重的指数移动平均(EMA)，衰减为0.9999。所有报告的结果均使用EMA模型。我们在所有DiT模型大小和补丁大小上使用相同的训练超参数。我们的训练超参数几乎完全从adm中保留下来。我们没有调整学习率、衰减/热身计划、Adam β1/β2或权重衰减。

扩散。我们使用来自稳定扩散[45]的现成的预训练变分自编码器(VAE)模型[27]。给定形状为256 × 256 × 3, z = E(x)形状为32 × 32 × 4的RGB图像x, VAE编码器的下采样因子为8。在本节的所有实验中，我们的扩散模型都在这个z空间中运行。在从我们的扩散模型中采样一个新的潜伏后，我们使用VAE解码器x = D(z)将其解码为像素。我们保留ADM[9]的扩散超参数：具体来说，我们使用$t_{max}=1000$线性方差表，范围为1×10⁻⁴到2 ×10⁻²,ADM的协方差参数化${\Sigma }_{\theta }$和他们嵌入输入时间步和标签的方法。

评价指标。我们用Fréchet初始距离(FID)[18]来衡量缩放性能，这是评估图像生成模型的标准度量。在与之前的工作进行比较时，我们遵循惯例，并使用250 DDPM采样步骤报告FID-50K。众所周知，FID对小的实现细节[34]非常敏感;为了保证比较的准确性，本文报告的所有值都是通过导出样本和使用ADM的TensorFlow评估套件[9]得到的。除非另有说明，本节中报告的FID编号不使用无分类器指导。我们还报告盗梦评分[48]，sFID[31]和精度/召回[29]作为次要指标。

计算。我们在JAX[1]中实现所有模型，并使用TPU-v3 pod进行训练。DiT-XL/2是我们最密集的计算模型，在全球批处理大小为256的TPU v3-256 pod上以大约5.7次/秒的速度训练。

5. 实验结果

DiT块设计。我们训练了四个最高的Gflop DiT-XL/2模型，每个模型都使用了不同的块设计——情境(119.4 Gflops)、交叉注意(137.6 Gflops)、自适应层范数(adaLN, 118.6 Gflops)或adaLN- 0 (118.6 Gflops)。我们在整个训练过程中测量FID。图5显示了结果。adaLN-Zero块产生的FID比交叉注意和上下文条件反射都要低，但计算效率最高。在400K训练迭代中，使用adaLN-Zero模型实现的FID几乎是上下文模型的一半，这表明调节机制严重影响模型质量。初始化也很重要——adalnzero将每个DiT块初始化为恒等函数，显著优于普通adaLN。F或其余的纸张，所有模型将使用adaLN-Zero DiT块。

缩放模型大小和补丁大小。我们训练了12个DiT模型，覆盖了模型配置(S, B, L, XL)和补丁大小(8,4,2)。注意，DiT-L和DiT-XL在相对gflop方面比其他配置明显更接近。图2(左)给出了每个模型的Gflops和它们在400K训练迭代时的FID的概述。在所有情况下，我们发现增加模型大小和减少补丁大小产生显著改善的扩散模型。图6(上)展示了FID如何随着模型大小的增加和补丁大小保持不变而变化。在所有四种配置中，通过使Transformer更深更宽，FID在所有训练阶段都得到了显著的改进。类似地，图6(下)显示了当补丁大小减小且模型大小保持不变时的FID。我们再次观察到在整个训练过程中，通过简单地扩大DiT处理的令牌数量，保持参数大约固定，FID有了很大的提高。

DiT gflop是提高性能的关键。图6的结果表明，参数计数在决定DiT模型的质量方面最终并不重要。当模型尺寸保持不变，patch尺寸减小时，Transformer的总参数实际上是不变的，只有Gflops增加。这些结果表明，缩放模型Gflops实际上是提高性能的关键。为了进一步研究这一点，我们将FID-50K在400K训练步骤中与模型Gflops绘制在图8中。结果表明，具有不同大小和令牌的DiT模型在其总Gflops相似(例如DiT- s /2和DiT- b /4)时最终获得相似的FID值。事实上，我们发现模型Gflops和FID-50K之间存在很强的负相关，这表明额外的模型计算是改进DiT模型的关键因素。在图12(附录)中，我们发现这一趋势也适用于其他指标，如Inception Score。

较大的DiT模型计算效率更高。在图9中，我们将FID绘制为所有DiT模型的总训练计算的函数。我们估计训练计算为模型Gflops·批大小·训练步骤·3，其中因子3大致近似于向后传递的计算量是向前传递的两倍。我们发现，即使训练时间较长，与训练步骤较少的大型DiT模型相比，小型DiT模型最终也会变得计算效率低下。类似地，我们发现除了补丁大小之外相同的模型即使在控制训练Gflops时也具有不同的性能配置文件。例如，XL/4在大约1010 Gflops后的性能优于XL/2。

可视化扩展。我们在图7中可视化缩放对样本质量的影响。在400K训练步骤中，我们使用相同的起始噪声xtmax、采样噪声和类标签从我们的12个DiT模型中采样一张图像。这让我们可以直观地解释缩放如何影响DiT样本质量。事实上，缩放模型大小和令牌数量在视觉质量上都有显著的改善。

5.1. State-of-the-Art Diffusion Models

256×256 ImageNet。在我们的缩放分析之后，我们继续训练我们最高的Gflop模型DiT-XL/2，用于7M步长。我们在图1中展示了该模型的样本，并将其与最先进的类条件生成模型进行了比较。我们在表2中报告结果。当使用无分类器制导时，DiT-XL/2优于所有先前的扩散模型，将先前由LDM实现的最佳FID-50K从3.60降低到2.27。图2(右)显示DiT-XL/2 (118.6 Gflops)相对于LDM-4 (103.6 Gflops)等潜在空间U-Net模型的计算效率更高，并且比ADM (1120 Gflops)或ADM- u (742 Gflops)等像素空间U-Net模型的效率更高。我们的方法实现了所有先前生成模型中最低的FID，包括先前最先进的StyleGANXL[50]。最后，我们还观察到，与LDM-4和LDM-8相比，DiT-XL/2在所有测试的无分类器引导量表上获得了更高的召回值。当只训练2.35M步长(类似于ADM)时，XL/2仍然优于所有先前的扩散模型，其FID为2.55。

512×512 ImageNet。我们在ImageNet上以512 × 512分辨率训练一个新的DiT-XL/2模型，用于3M迭代，其超参数与256 × 256模型相同。在补丁大小为2的情况下，这个XL/2模型在对64 × 64 × 4输入潜在值(524.6 Gflops)进行补丁后，总共处理1024个令牌。表3显示了与最先进方法的比较。XL/2在此分辨率下再次优于所有先前的扩散模型，将ADM的最佳FID从3.85提高到3.04。即使增加了令牌数量，XL/2仍然保持计算效率。例如，ADM使用1983个gflop, ADM- u使用2813个gflop;XL/2使用524.6 gflop。我们在图1和附录中展示了来自高分辨率XL/2模型的样本。

5.2. Model Compute vs. Sampling Compute

与大多数生成模型不同，扩散模型的独特之处在于，它们可以在生成图像时通过增加采样步骤的数量来训练后使用额外的计算。考虑到模型Gflops在样本质量中的重要性，在本节中，我们将研究较小的模型计算dit是否可以通过使用更多的抽样计算来优于较大的dit。我们在400K训练步骤后计算所有12个DiT模型的FID，每张图像使用[16,32,64,128,256,1000]采样步骤。主要结果如图10所示。考虑使用1000个采样步骤的DiT-L/2与使用128个采样步骤的DiT-XL/2。在这种情况下，L/2使用80.7 tflop对每张图像进行采样;XL/2使用5倍少的计算量- 15.2 tflop -对每张图像进行采样。尽管如此，XL/2具有更好的FID-10K (23.7 vs 25.9)。一般来说，抽样计算不能弥补模型计算的不足。

6. 结论

我们介绍了扩散Transformer(DiTs)，这是一种简单的基于Transformer的扩散模型骨干，优于先前的U-Net模型，并继承了Transformer模型类的优秀缩放特性。鉴于本文中有希望的扩展结果，未来的工作应该继续将dit扩展到更大的模型和令牌数量。DiT还可以作为文本-图像模型(如DALL·e2和稳定扩散模型)的主干进行探索。

A. 其他实施细节

我们在表4中包含了关于所有DiT模型的信息，包括256 × 256和512 × 512模型。我们包括Gflop计数，参数，训练细节，fid等。我们还在表6中包括了来自ADM和LDM的DDPM U-Net模型的Gflop计数。DiT模型细节。为了嵌入输入时间步长，我们使用256维频率嵌入[9]，然后使用两层MLP，其维度等于Transformer的隐藏大小和SiLU激活。每个adaLN层将时间步长和类嵌入的和馈送到一个SiLU非线性层和一个线性层，输出神经元等于Transformer的隐藏大小的4× (adaLN)或6× (adaLN- 0)。我们在核心Transformer[16]中使用了GELU非线性(近似于tanh)。

B. VAE解码器消融

我们在实验中使用了现成的、预先训练好的V AEs。V AE模型(ft-MSE和ft-EMA)是原始LDM“f8”模型的微调版本(只有解码器权重进行了微调)。在第5节中，我们使用ft-MSE解码器来监控缩放分析的指标，我们使用ft-EMA解码器来处理表2和表3中报告的最终指标。在本节中，我们去掉了三种不同的V AE解码器的选择;LDM使用的原始译码器和Stable Diffusion使用的两个微调译码器。因为编码器在模型中是相同的，解码器可以在不重新训练扩散模型的情况下被替换。表5显示了结果;当使用LDM解码器时，XL/2优于所有先前的扩散模型。

C. 模型样本

我们展示了来自两个DiT-XL/2模型的样本，分别在512 × 512和256 × 256分辨率下训练3M和7M步长。图1和11显示了从两个模型中选取的样本。图13到32显示了两个模型在一系列分类器自由引导尺度和输入类别标签(使用250 DDPM采样步骤和ft-EMA VAE解码器生成)上的非策展样本。与之前使用指导的工作一样，我们观察到更大的尺度增加了视觉保真度，减少了样本多样性。

256 × 256分辨率下训练3M和7M步长。图1和11显示了从两个模型中选取的样本。图13到32显示了两个模型在一系列分类器自由引导尺度和输入类别标签(使用250 DDPM采样步骤和ft-EMA VAE解码器生成)上的非策展样本。与之前使用指导的工作一样，我们观察到更大的尺度增加了视觉保真度，减少了样本多样性。

文章来源地址https://www.toymoban.com/news/detail-650403.html

到了这里，关于Scalable Diffusion Models with Transformers的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！