29 深度玻尔兹曼机
29.1 背景介绍
过去在解决BM问题的时候，提出过多种模型：RBM、SBN、DBN
- 其中RBM是一种有限制条件的，简化的BM，限制了隐藏层和观测层内部都没有连接。实质上是一种特殊的BM。
- SBN实际上就是一种多层的有向图结构，是为了方便我们通过sigmoid函数采样构造出来的。
- DBN本质上是想通过叠加RBM实现多层结构，但是由于条件限制，使得DBN的实际结构为RBM+SBN，所以DBN实际上并非一个BM
而现在的DBM则是实际的多层RBM结构，也是一种特殊的BM。
29.2 DBM的叠加方式
DBM实际上就是直接conbine多层RBM，如我们有三层结构：
v
,
h
(
1
)
,
h
(
2
)
v, h(1), h(2)
v,h(1),h(2)，我们将
v
,
h
(
1
)
v, h(1)
v,h(1)划为一个RBM，将
h
(
1
)
,
h
(
2
)
h(1), h(2)
h(1),h(2)划为一个RBM，则我们可以得到公式：
{
P
(
V
)
=
∑
h
(
1
)
P
(
v
,
h
(
1
)
)
=
∑
h
(
1
)
P
(
h
(
1
)
;
w
(
1
)
)
‾
⋅
P
(
v
∣
h
(
1
)
;
w
(
1
)
)
P
(
h
(
1
)
;
w
(
2
)
)
‾
=
∑
h
(
2
)
P
(
h
(
1
)
,
h
(
2
)
;
w
(
2
)
)
\begin{cases} P(V) = \sum_{h^{(1)}} P(v, h^{(1)}) = \sum_{h^{(1)}} \underline{P(h^{(1)}; w^{(1)})} \cdot P(v| h^{(1)}; w^{(1)}) \\ \underline{P(h^{(1)}; w^{(2)})} = \sum_{h^{(2)}} P(h^{(1)}, h^{(2)}; w^{(2)}) \end{cases}
{P(V)=∑h(1)P(v,h(1))=∑h(1)P(h(1);w(1))⋅P(v∣h(1);w(1))P(h(1);w(2))=∑h(2)P(h(1),h(2);w(2))
我们的DBM实际上就是想要通过
P
(
h
(
1
)
;
w
(
2
)
)
P(h^{(1)}; w^{(2)})
P(h(1);w(2))（以
w
(
2
)
w^{(2)}
w(2)为参数的
P
(
h
(
1
)
)
P(h^{(1)})
P(h(1))）替换
P
(
h
(
1
)
;
w
(
1
)
)
P(h^{(1)}; w^{(1)})
P(h(1);w(1))。
不过这样我们简单想想也知道容易出问题，他可能会产生double counting problem，因为在这样直接替换的过程中也是在不断的重复利用样本数据，所以会导致目标分布尖锐。
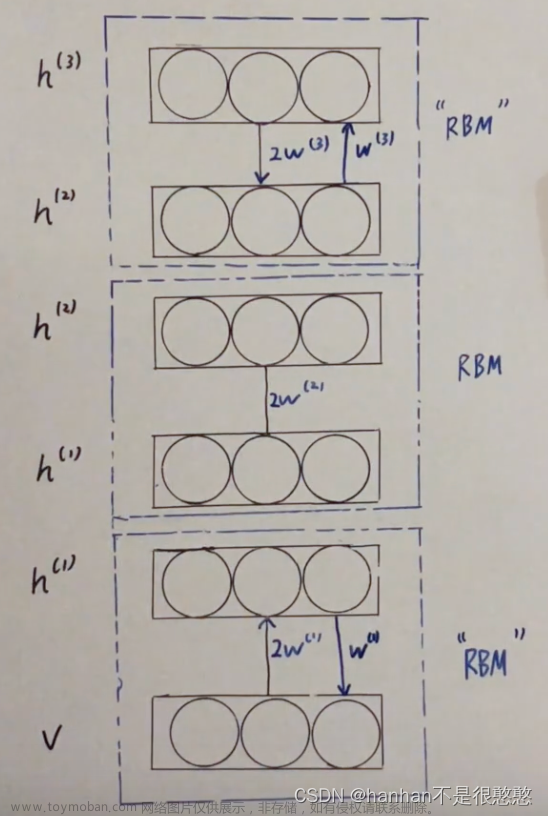
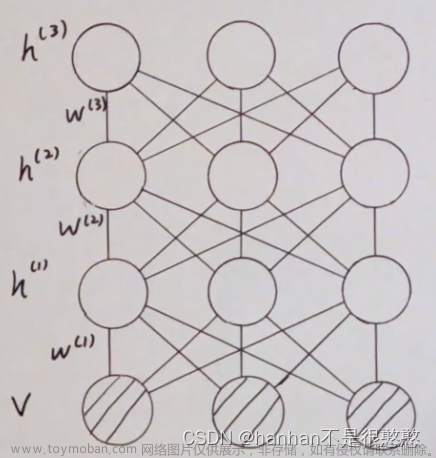
具体的参数学习我们是将 w ( 1 ) , w ( 2 ) w^{(1)}, w^{(2)} w(1),w(2)分别取一半（类似求平均数），得出来的结果图为：
文章来源：https://www.toymoban.com/news/detail-650935.html
我们在这将参数设置为两倍，是为了使目标图形的参数为单倍。然后我们发现首尾的RBM不一样，这两个变形的RBM是因为第一层和最后一层只有一个输入（如 h ( 1 ) h^{(1)} h(1)有 v v v和 h ( 2 ) h^{(2)} h(2)，但 v v v只有 h ( 1 ) h^{(1)} h(1)），所以和其他不一样。文章来源地址https://www.toymoban.com/news/detail-650935.html
到了这里，关于29 深度玻尔兹曼机的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
