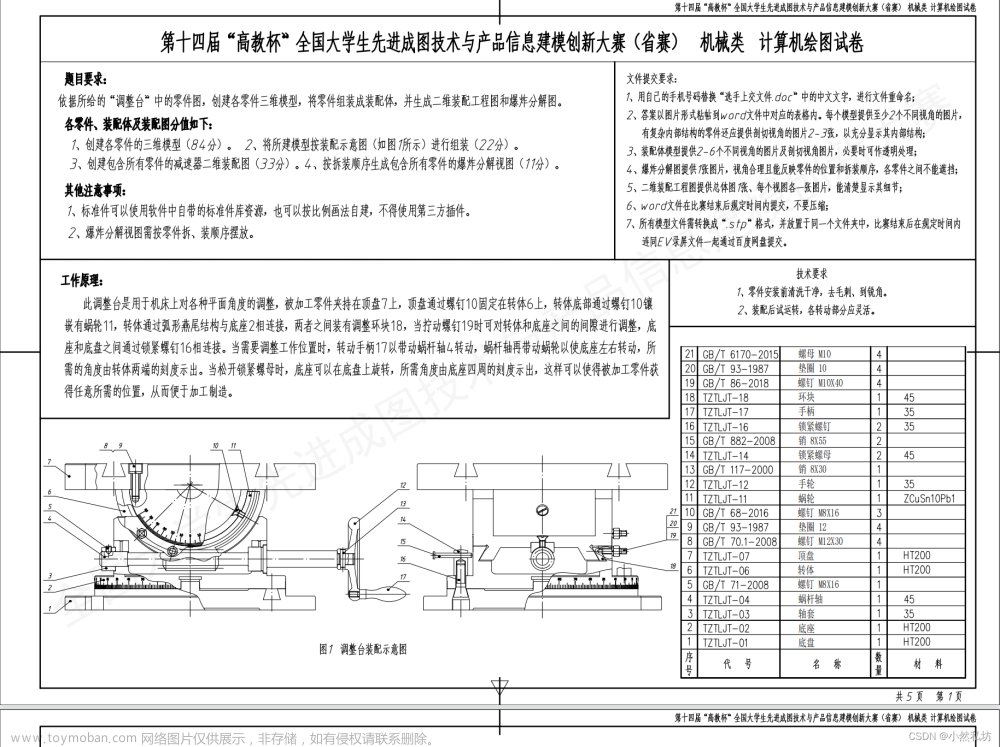
第一问
第二问
1、A评级客户流失率相对误差
% 需要论文和代码,请联系:isfuture@outlook.com
2、B评级客户流失率相对误差
% 需要论文和代码,请联系:isfuture@outlook.com
clear;
X = [0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y = [0.447704483 0.094809717 -0.042357953 -0.1093183 -0.029504019 -0.08177512 -0.05374639 -0.067354229 -0.078529943 -0.066123709 -0.004042344 -0.010993686 -0.014989933 0.020250078 0.007373335 0.013539864 0.037840941 0.016710394 -0.000100478 0.043073939 0.024437232 0.011348263 0.015418915 0.009166262 0.002801528 0.009866109 -0.021299217 -0.044380264
];
scatter(X, Y, 20,'filled');
% axis([1 2 1 2]);
ylim([-0.35 0.35]);
xlabel('贷款年利率');
ylabel('客户流失率相对误差');
title('B评级客户流失率相对误差');
3、C评级客户流失率相对误差
%% 需要论文和代码,请联系:isfuture@outlook.com
clear;
X = [0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y = [0.241022873 0.132760257 0.045307686 -0.107807025 -0.02105494 -0.061770852 -0.047328371 -0.100791547 -0.080190917 -0.037289585 0.004480784 -0.034160824 0.020210034 -0.013643313 0.008513513 -0.006049881 -0.000383586 0.042776403 0.018494763 0.009725945 0.021647558 0.026102498 0.011434163 0.008849048 0.003877692 0.018148552 -0.020697357 -0.04726721
];
scatter(X, Y, 20,'filled');
% axis([1 2 1 2]);
ylim([-0.35 0.35]);
xlabel('贷款年利率');
ylabel('客户流失率相对误差');
title('C评级客户流失率相对误差');
4、金额图
% 需要论文和代码,请联系:isfuture@outlook.com
5、利率图
X = [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 37 38 39 40 41 42 43 44 46 47 48 49 50 51 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 83 84 85 86 88 89 90 91 92 93 94 95 96 97 98 104 105 106 110
];
Y=[0.04469888 0.107693406 0.096619827 0.144685372 0.06636303 0.116944557 0.069812132 0.05061235 0.078094652 0.083281223 0.099200728 0.140004869 0.091563938 0.069765165 0.06788777 0.064739764 0.108193238 0.075133482 0.126360685 0.052800813 0.083106487 0.128767168 0.080650381 0.094275505 0.049011169 0.138551071 0.083023976 0.071178613 0.136069627 0.121975718 0.127088231 0.051643079 0.096493128 0.096395806 0.116349402 0.119465089 0.119493027 0.140231878 0.059490346 0.127780826 0.096021022 0.041814038 0.064495806 0.093069603 0.068412479 0.055995192 0.094441436 0.067372248 0.055106626 0.055108386 0.093345062 0.079170723 0.137030095 0.042081024 0.107283791 0.104653562 0.127604769 0.086307113 0.042951928 0.105569879 0.12013018 0.139460741 0.090264797 0.093717376 0.07826072 0.115461523 0.06138162 0.097924008 0.059309414 0.122929398 0.072518809 0.148251397 0.047491648 0.075253214 0.103024773 0.053933738 0.108433576 0.128485428 0.140770949 0.04237487 0.050250473 0.060157075 0.0762983 0.067692723 0.068172086 0.103401843 0.09293262 0.064891824 0.082360703 0.061259464 0.079560398 0.082533283 0.110705129 0.08238775 0.044939352 0.071069688 0.086866292
];
plot(X, Y);
% axis([1 2 1 2]);
ylim([0.03 0.16]);
xlabel('企业代号');
ylabel('贷款利率');
title('各企业贷款利率');
6、模拟A等级曲线
@[TOC]
# 第一问
# 第二问
## 1、A评级客户流失率相对误差
```c
% 需要论文和代码,请联系:isfuture@outlook.com
clear;
X = [0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y = [0.309554608 0.302980047 0.017579194 -0.076669863 -0.056297703 -0.092750467 -0.060296874 -0.065628885 -0.007390326 -0.044560631 -0.037774003 -0.045669423 -0.014690112 -0.006554997 0.017250496 0.023616607 -0.001116445 -0.000927442 0.03507357 0.026073175 0.046149231 0.011734214 0.005247229 0.012198912 0.00041122 0.014946501 -0.018942205 -0.044111182
];
scatter(X, Y, 20,'filled');
% axis([1 2 1 2]);
ylim([-0.35 0.35]);
xlabel('贷款年利率');
ylabel('客户流失率相对误差');
title('A评级客户流失率相对误差');
2、B评级客户流失率相对误差
% 需要论文和代码,请联系:isfuture@outlook.com
clear;
X = [0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y = [0.447704483 0.094809717 -0.042357953 -0.1093183 -0.029504019 -0.08177512 -0.05374639 -0.067354229 -0.078529943 -0.066123709 -0.004042344 -0.010993686 -0.014989933 0.020250078 0.007373335 0.013539864 0.037840941 0.016710394 -0.000100478 0.043073939 0.024437232 0.011348263 0.015418915 0.009166262 0.002801528 0.009866109 -0.021299217 -0.044380264
];
scatter(X, Y, 20,'filled');
% axis([1 2 1 2]);
ylim([-0.35 0.35]);
xlabel('贷款年利率');
ylabel('客户流失率相对误差');
title('B评级客户流失率相对误差');
3、C评级客户流失率相对误差
%% 需要论文和代码,请联系:isfuture@outlook.com
clear;
X = [0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y = [0.241022873 0.132760257 0.045307686 -0.107807025 -0.02105494 -0.061770852 -0.047328371 -0.100791547 -0.080190917 -0.037289585 0.004480784 -0.034160824 0.020210034 -0.013643313 0.008513513 -0.006049881 -0.000383586 0.042776403 0.018494763 0.009725945 0.021647558 0.026102498 0.011434163 0.008849048 0.003877692 0.018148552 -0.020697357 -0.04726721
];
scatter(X, Y, 20,'filled');
% axis([1 2 1 2]);
ylim([-0.35 0.35]);
xlabel('贷款年利率');
ylabel('客户流失率相对误差');
title('C评级客户流失率相对误差');
4、金额图
% 需要论文和代码,请联系:isfuture@outlook.com
X = [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 37 38 39 40 41 42 43 44 46 47 48 49 50 51 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 83 84 85 86 88 89 90 91 92 93 94 95 96 97 98 104 105 106 110
];
Y=[96.09256621 62.92096242 87.26917098 85.40369545 49.4773881 45.47527427 85.8468782 48.37472738 82.29843514 62.46964367 40.04966899 94.20618175 52.48648768 25.7092855 93.46826675 57.03208207 77.68674466 93.06778901 42.44205961 31.88137146 61.45602364 92.55863128 93.45820869 35.79336892 48.71468183 48.85516538 96.80882815 25.28178114 48.47810187 88.35881261 72.65022186 82.41694495 93.22000663 98.61064552 66.48678977 91.6189466 40.41252055 96.02059094 37.05275933 63.82392609 84.26330175 99.67044485 71.21717471 80.33484345 62.47731646 76.92284993 54.63021415 58.10043624 41.00234442 95.87078924 43.17394839 50.68348758 37.14170246 74.25088491 44.57958933 83.86201486 75.86626122 86.91810459 54.41480306 24.41652558 87.38655562 83.57750051 40.90327845 85.66731091 96.19076752 42.76286987 56.53812568 93.17888594 82.09517174 36.87571381 66.83639565 68.50537571 29.27377556 44.40851517 78.7151542 39.48243457 30.06297082 41.61679352 47.58691255 79.25325903 84.08786715 94.97133833 91.02132601 91.31838535 51.70416706 19.2331108 51.46526851 43.38370108 72.77267053 92.84116712 51.1658314 46.26955569 94.12684682 91.17750621 48.4143125 49.973333 96.52759109
];
plot(X, Y);
% axis([1 2 1 2]);
ylim([10 110]);
xlabel('企业代号');
ylabel('贷款金额/万元');
title('各企业贷款金额');
5、利率图
X = [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 37 38 39 40 41 42 43 44 46 47 48 49 50 51 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 83 84 85 86 88 89 90 91 92 93 94 95 96 97 98 104 105 106 110
];
Y=[0.04469888 0.107693406 0.096619827 0.144685372 0.06636303 0.116944557 0.069812132 0.05061235 0.078094652 0.083281223 0.099200728 0.140004869 0.091563938 0.069765165 0.06788777 0.064739764 0.108193238 0.075133482 0.126360685 0.052800813 0.083106487 0.128767168 0.080650381 0.094275505 0.049011169 0.138551071 0.083023976 0.071178613 0.136069627 0.121975718 0.127088231 0.051643079 0.096493128 0.096395806 0.116349402 0.119465089 0.119493027 0.140231878 0.059490346 0.127780826 0.096021022 0.041814038 0.064495806 0.093069603 0.068412479 0.055995192 0.094441436 0.067372248 0.055106626 0.055108386 0.093345062 0.079170723 0.137030095 0.042081024 0.107283791 0.104653562 0.127604769 0.086307113 0.042951928 0.105569879 0.12013018 0.139460741 0.090264797 0.093717376 0.07826072 0.115461523 0.06138162 0.097924008 0.059309414 0.122929398 0.072518809 0.148251397 0.047491648 0.075253214 0.103024773 0.053933738 0.108433576 0.128485428 0.140770949 0.04237487 0.050250473 0.060157075 0.0762983 0.067692723 0.068172086 0.103401843 0.09293262 0.064891824 0.082360703 0.061259464 0.079560398 0.082533283 0.110705129 0.08238775 0.044939352 0.071069688 0.086866292
];
plot(X, Y);
% axis([1 2 1 2]);
ylim([0.03 0.16]);
xlabel('企业代号');
ylabel('贷款利率');
title('各企业贷款利率');
6、模拟A等级曲线
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
YY = [];
A = -200:0.1:-190;
B = -15:0.1:-11;
C = 14:0.1:16;
D = -1:0.1:1;
E = [];
XA = [];
XC=[];
XB=[];
XD=[];
XX = [];
ii = 0;
e = 0;
for i=1:length(A)
a=A(i);
for j=1:length(B)
b=B(j);
for p=1:length(D)
d=D(p);
for k=1:length(C)
c=C(k);
e = 0;
for s=1:length(X)
x=X(s);
f = a*x^3+b*x^2+c*x+d;
e = e+(f-Y1(s))^2;
end
if e < 0.02255
ii = ii + 1;
XA(ii) =a;
XB(ii)=b;
XC(ii)=c;
XD(ii)=d;
XX(ii) = ii;
E(ii) = e;
end
end
end
end
end
[~,position]=min(E);
XA(position)
XB(position)
XC(position)
XD(position)
plot(XX, E);
7、模拟B等级曲线
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
Y2=[0 0.066799583 0.13505206 0.20658008 0.276812293 0.302883401 0.370215852 0.406296668 0.458295295 0.508718692 0.544408837 0.548493958 0.588765696 0.625764576 0.635605146 0.673527424 0.696925431 0.705315993 0.742936326 0.776400729 0.762022595 0.791503697 0.814998933 0.822297861 0.835301602 0.845747745 0.842070844 0.868159536 0.885864919];
Y3=[0 0.068725306 0.122099029 0.181252146 0.263302863 0.290189098 0.34971559 0.390771683 0.45723807 0.492660433 0.513660239 0.530248706 0.587762408 0.590097045 0.642993656 0.658839416 0.696870573 0.719103552 0.711101237 0.750627656 0.776816043 0.784480512 0.795566274 0.820051434 0.832288422 0.844089875 0.836974326 0.872558957 0.895164739];
A = -200:0.1:-190;
B = -10:0.1:-8;
C = 14:0.1:16;
D = -1:0.1:1;
E = [];
XA = [];
XC=[];
XB=[];
XD=[];
XX = [];
ii = 0;
e = 0;
for i=1:length(A)
a=A(i);
for j=1:length(B)
b=B(j);
for p=1:length(D)
d=D(p);
for k=1:length(C)
c=C(k);
e = 0;
for s=1:length(X)
x=X(s);
f = a*x^3+b*x^2+c*x+d;
e = e+(f-Y2(s))^2;
end
if e < 0.02255
ii = ii + 1;
XA(ii) =a;
XB(ii)=b;
XC(ii)=c;
XD(ii)=d;
XX(ii) = ii;
E(ii) = e;
end
end
end
end
end
[~,position]=min(E);
XA(position)
XB(position)
XC(position)
XD(position)
plot(XX, E);
8、模拟C等级曲线
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
Y2=[0 0.066799583 0.13505206 0.20658008 0.276812293 0.302883401 0.370215852 0.406296668 0.458295295 0.508718692 0.544408837 0.548493958 0.588765696 0.625764576 0.635605146 0.673527424 0.696925431 0.705315993 0.742936326 0.776400729 0.762022595 0.791503697 0.814998933 0.822297861 0.835301602 0.845747745 0.842070844 0.868159536 0.885864919];
Y3=[0 0.068725306 0.122099029 0.181252146 0.263302863 0.290189098 0.34971559 0.390771683 0.45723807 0.492660433 0.513660239 0.530248706 0.587762408 0.590097045 0.642993656 0.658839416 0.696870573 0.719103552 0.711101237 0.750627656 0.776816043 0.784480512 0.795566274 0.820051434 0.832288422 0.844089875 0.836974326 0.872558957 0.895164739];
A = -165:0.1:-160;
B = -15:0.1:-10;
C = 14:0.1:16;
D = -1:0.1:1;
E = [];
XA = [];
XC=[];
XB=[];
XD=[];
XX = [];
ii = 0;
e = 0;
for i=1:length(A)
a=A(i);
for j=1:length(B)
b=B(j);
for p=1:length(D)
d=D(p);
for k=1:length(C)
c=C(k);
e = 0;
for s=1:length(X)
x=X(s);
f = a*x^3+b*x^2+c*x+d;
e = e+(f-Y3(s))^2;
end
if e < 0.02255
ii = ii + 1;
XA(ii) =a;
XB(ii)=b;
XC(ii)=c;
XD(ii)=d;
XX(ii) = ii;
E(ii) = e;
end
end
end
end
end
[~,position]=min(E);
XA(position)
XB(position)
XC(position)
XD(position)
plot(XX, E);
09、信誉评级A客户流失率实际值与预测曲线
clear;
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
a=-194.7;
b=-13.4;
c=15.6;
d=-0.5;
for i=1:length(X)
x=X(i);
f = a*x^3+b*x^2+c*x+d;
F(i) = f;
end
plot(X, Y1, '*');
hold on;
plot(X, F, 'r','linewidth', 2);
axis([0.02 0.18 0 1]);
xlabel('贷款年利率');
ylabel('信誉评级A客户流失率');
title('信誉评级A客户流失率实际值与预测曲线');
legend('实际值' ,'预测曲线');
10、信誉评级B客户流失率实际值与预测曲线
clear;
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y2=[0 0.066799583 0.13505206 0.20658008 0.276812293 0.302883401 0.370215852 0.406296668 0.458295295 0.508718692 0.544408837 0.548493958 0.588765696 0.625764576 0.635605146 0.673527424 0.696925431 0.705315993 0.742936326 0.776400729 0.762022595 0.791503697 0.814998933 0.822297861 0.835301602 0.845747745 0.842070844 0.868159536 0.885864919];
a=-194.8;
b=-9.6;
c=14.8;
d=-0.5;
for i=1:length(X)
x=X(i);
f = a*x^3+b*x^2+c*x+d;
F(i) = f;
end
plot(X, Y2, '*');
hold on;
plot(X, F, 'r','linewidth', 2);
axis([0.02 0.18 0 1]);
xlabel('贷款年利率');
ylabel('信誉评级B客户流失率');
title('信誉评级B客户流失率实际值与预测曲线');
legend('实际值' ,'预测曲线');
11、信誉评级C客户流失率实际值与预测曲线
clear;
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y3=[0 0.068725306 0.122099029 0.181252146 0.263302863 0.290189098 0.34971559 0.390771683 0.45723807 0.492660433 0.513660239 0.530248706 0.587762408 0.590097045 0.642993656 0.658839416 0.696870573 0.719103552 0.711101237 0.750627656 0.776816043 0.784480512 0.795566274 0.820051434 0.832288422 0.844089875 0.836974326 0.872558957 0.895164739];
a=-159.7;
b=-14.5;
c=14.8;
d=-0.5;
F = [];
for i=1:length(X)
x=X(i);
f = a*x^3+b*x^2+c*x+d;
F(i) = f;
end
plot(X, Y3, '*');
hold on;
plot(X, F, 'r','linewidth', 2);
axis([0.02 0.18 0 1]);
xlabel('贷款年利率');
ylabel('信誉评级C客户流失率');
title('信誉评级C客户流失率实际值与预测曲线');
legend('实际值' ,'预测曲线');
12、求最优解
clear;
a1=-194.7;
b1=-13.4;
c1=15.6;
d1=-0.5;
a2=-194.8;
b2=-9.6;
c2=14.8;
d2=-0.5;
a3=-159.7;
b3=-14.5;
c3=14.8;
d3=-0.5;
% 代号-得分-等级
E_Z_DJ = [
1 0.1172 9
2 0.1173 9
12 0.5834 7
25 0.1163 7
34 0.1151 7
38 0.1841 7
45 0.1447 7
47 0.1157 7
49 0.1167 7
53 0.1155 7
56 0.1155 7
60 0.1579 7
61 0.2009 7
62 0.8322 7
63 0.1165 7
64 0.1061 5
66 0.113 5
69 0.3324 5
71 0.1166 7
73 0.1161 7
75 0.1152 7
76 0.1263 5
77 0.1157 7
78 0.1161 7
80 0.1138 5
82 0.1178 7
86 0.1148 7
87 0.1132 5
88 0.1146 5
89 0.1188 5
90 0.1156 7
91 0.1153 7
92 0.1142 5
93 0.1124 5
94 0.1058 5
95 0.1098 5
96 0.1111 5
98 0.1129 5
99 0.1138 7
100 0.1122 5
102 0.1164 7
103 0.1382 7
104 0.1662 7
105 0.1147 7
106 0.1156 7
107 0.1149 5
108 0.1128 5
109 0.1149 7
110 0.1129 5
111 0.1132 5
112 0.1134 5
113 0.1126 5
114 0.1111 5
115 0.1134 5
116 0.1125 5
117 0.1068 5
118 0.1134 5
119 0.1062 5
120 0.1134 5
121 0.1118 5
122 0.1126 5
123 0.1709 5
124 0.1128 5
125 0.1123 5
126 0.113 5
127 0.1123 5
128 0.1381 5
129 0.1127 5
130 0.112 5
131 0.1141 5
132 0.1126 5
133 0.1145 5
134 0.1124 5
135 0.113 5
136 0.1119 5
137 0.1127 5
138 0.1128 5
139 0.1134 5
140 0.112 5
141 0.1057 5
142 0.1118 5
143 0.1132 5
144 0.1136 5
145 0.1333 5
146 0.1126 5
147 0.1119 5
148 0.1115 5
149 0.1123 5
150 0.1148 5
151 0.1153 5
152 0.1117 5
153 0.1116 5
154 0.1129 5
155 0.1128 5
156 0.1127 5
157 0.1132 5
158 0.1129 5
159 0.1115 5
160 0.1132 5
161 0.1126 5
162 0.1118 5
163 0.1115 5
164 0.1119 5
165 0.1118 5
166 0.1133 5
167 0.1127 5
168 0.1113 5
169 0.1141 5
170 0.1133 5
171 0.1125 5
172 0.1118 5
173 0.1115 5
174 0.1124 5
175 0.1192 5
176 0.1126 5
177 0.1125 5
178 0.1128 5
179 0.1123 5
180 0.1129 5
181 0.1135 5
182 0.1127 5
183 0.1123 5
184 0.1123 5
185 0.1128 5
186 0.1116 5
187 0.1129 5
188 0.1122 5
189 0.1129 5
190 0.113 5
191 0.1121 5
192 0.1145 5
193 0.1125 5
194 0.1117 5
195 0.1127 5
196 0.1139 5
197 0.1127 5
198 0.1144 5
199 0.1128 5
200 0.1108 5
201 0.1118 5
202 0.1156 5
203 0.1127 5
204 0.1129 5
205 0.1123 5
206 0.5633 5
207 0.1166 5
208 0.1126 5
209 0.1132 5
210 0.1129 5
211 0.113 5
212 0.1123 5
213 0.1165 5
214 0.1155 5
215 0.1131 5
216 0.1133 5
217 0.1143 5
218 0.1134 5
219 0.1118 5
220 0.1545 5
221 0.1126 5
222 0.1124 5
223 0.1132 5
224 0.1152 5
225 0.1206 5
226 0.1151 5
227 0.1123 5
228 0.1125 5
229 0.1126 5
230 0.1117 5
231 0.1139 5
232 0.1574 5
233 0.1633 5
234 0.13 5
235 0.1844 5
236 0.134 5
237 0.2421 5
238 0.1118 5
239 0.1123 5
240 0.118 5
241 0.1132 5
242 0.1124 5
243 0.1138 5
244 0.1213 5
245 0.1107 5
246 0.1129 5
247 0.2526 5
248 0.1121 5
249 0.1134 5
250 0.1133 5
251 0.1351 5
252 0.2107 5
253 0.1157 5
254 0.1305 5
255 0.112 5
256 0.1105 5
257 0.1711 5
258 0.1115 5
259 0.1821 5
260 0.1164 5
261 0.112 5
262 0.1086 5
263 0.1119 5
264 0.1198 5
265 0.1219 5
266 0.1186 5
267 0.1138 5
268 0.1562 5
269 0.114 5
270 0.1426 5
271 0.1075 5
272 0.1107 5
273 0.1123 5
274 0.1166 5
275 0.1139 5
276 0.1128 5
277 0.1208 5
278 0.1101 5
279 0.1121 5
280 0.1127 5
281 0.1109 5
282 0.1103 5
283 0.1122 5
284 0.1109 5
285 0.1121 5
286 0.1154 5
287 0.1149 5
288 0.1122 5
289 0.1139 5
290 0.1139 5
291 0.1124 5
292 0.2104 5
293 0.1129 5
294 0.1135 5
295 0.1126 5
296 0.1133 5
297 0.113 5
298 0.1139 5
299 0.1153 5
300 0.1122 5
301 0.1179 5
302 0.1098 5
];
E = E_Z_DJ(:, 1);
DJ = E_Z_DJ(:, 3);
Z = E_Z_DJ(:, 2);
fun_range = [0,3.08;0,2.1]; %每个维度的求解范围,行代表维度,第一列最小值,第二列最大值
density = 0.01; %图像中取点的密度
d = 2; %维度
popsize = 10; %种群大小
maxgen = 100; %最大迭代次数
limit_v = 10; %最大运动速度
maxormin = 0; %求最大值还是最小值。最大值为1,最小值为0
dynamic = 1; %是否采用动态参数
W = [0.7,1.4]; %惯性因子
C2 = [0.5,2.5];
C1 = [0.5,2.5]; %学习因子。
ZZ = pso1_im(funct,fun_range,density,d);
[x,v,fitness,pbest,gbest,gbest_fitness,gbest_index,pbest_fitness] =...
pso1_in(funct,popsize,d,fun_range,limit_v,maxormin);
[gbest_fitness,gbest_index,record] =...
pso1_in2(funct,d,popsize,maxgen,dynamic,W,C1,C2,fun_range,limit_v,density...
,x,v,fitness,pbest,gbest,gbest_fitness,gbest_index,pbest_fitness,maxormin);
% sigma = 4:1:15; 年利率
% D = 10:1:100; % 投放金额
T = 1; %周期为 1 年
M = 10000; % 总贷款额度1亿
Sigma = [];
DD = [];
Beta = [];
W = []; % 利润,即最大化目标
Z_S = ones(1, length(E)); % 每个利率 1不用管
Z_D = ones(1, length(E)); % 每个投资
N = 10000; % 迭代次数
nnn = 0;
for i=1:1:N
Sigma = []; % 该次遍历的利率
DD = []; % 该次遍历的贷款
w = 0; % 该次遍历的目标值
for j=1:length(E)
Sigma(j) = 0.04 + (0.15-0.04).*rand(1,1);
x = Sigma(j);
DD(j) = 10 + (100-10).*rand(1,1);
d = DD(j);
if DJ(j) == 1
Beta(j) = a1*x^3+b1*x^2+c1*x+d1;
elseif DJ(j) == 2
Beta(j) = a2*x^3+b2*x^2+c2*x+d2;
else
Beta(j) = a3*x^3+b3*x^2+c3*x+d3;
end
w = w + d*x*(1-Beta(j))*Z(j);
end
if w > 60
nnn = nnn+1;
W(nnn) = w;
Z_S(nnn,:) = Sigma(:);
Z_D(nnn,:) = DD(:);
end
end
XX = 1:1:nnn;
plot(XX, W, '*');
for i=1:length(Z_S(:, 1))
sum(Z_D(i,:))
end
13、神经网络
import numpy as np
import pandas as pd
import time
import tensorflow.compat.v1 as tf # 本行报错不用处理
tf.disable_v2_behavior()
# 图网络 和 生成对抗网络
IN_DIV = 24 # 输入维度
OUT_DIV = 4 # 输出维度
nIter = 10000 # 迭代次数为 10000 次
speed = 0.08
N = 100 # 每层神经元个数
NATrain = 25 # 每一类的训练样本数
NBTrain = 25
NCTrain = 30
NDTrain = 20
NATest = 2 # 每一类的测试样本数
NBTest = 13
NCTest = 4
NDTest = 4
# 数据集导入
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
train = np.array(train)
test = np.array(test)
def noramlization(data):
minVals = data.min(0)
maxVals = data.max(0)
ranges = maxVals - minVals
normData = np.zeros(np.shape(data))
m = data.shape[0]
normData = data - np.tile(minVals, (m, 1))
normData = normData/np.tile(ranges, (m, 1))
return normData, ranges, minVals
A_train = train[0:NATrain, :]
B_train = train[NATrain:NATrain+NBTrain, :]
C_train = train[NATrain+NBTrain:NATrain+NBTrain+NCTrain, :]
D_train = train[NATrain+NBTrain+NCTrain:, :]
A_test = test[0:NATest, :]
B_test = test[NATest:NATest+NBTest, :]
C_test = test[NATest+NBTest:NATest+NBTest+NCTest, :]
D_test = test[NATest+NBTest+NCTest:, :]
# 数据格式化
X_train = np.vstack((A_train, B_train, C_train, D_train))
X_test = np.vstack((A_test, B_test, C_test, D_test))
train_label = np.matrix([[1, 0, 0, 0]] * NATrain + [[0, 1, 0, 0]] * NBTrain + [[0, 0, 1, 0]] * NCTrain + \
[[0, 0, 0, 1]] * NDTrain)
test_label = np.matrix([[1, 0, 0, 0]] * NATest + [[0, 1, 0, 0]] * NBTest + [[0, 0, 1, 0]] * NCTest + \
[[0, 0, 0, 1]] * NDTest)
print(test_label)
'''
我们采用三层前向神经网络来优化这个任务, 其中每层的神经元个数取20,
初始化取 xavier initialization,优化处理器取 GradientDescentOptimizer,
学习率取 0.001, 激活函数选取 sigmoid 函数, 迭代次数为 1000.
'''
layers = [IN_DIV, N, N, N, OUT_DIV] # 输入层 2 个维度,中间层为 3 层,每层 20 个神经元,输出层维度为 5,因为要分为 5 类
# define neural network structure
# tf.palceholder
x_tf = tf.placeholder(tf.float32, shape=[None, X_train.shape[1]])
y_tf = tf.placeholder(tf.float32, shape=[None, train_label.shape[1]])
def initialize_NN(layers):
weights = [] # 权重矩阵
biases = [] # 截距矩阵 Y = W*X + b
num_layers = len(layers)
for l in range(0, num_layers - 1):
W = xavier_init(size=[layers[l], layers[l + 1]])
b = tf.Variable(tf.zeros([1, layers[l + 1]], dtype=tf.float32), dtype=tf.float32)
weights.append(W)
biases.append(b)
return weights, biases
def xavier_init(size):
in_dim = size[0] # 第 n 层的维度
out_dim = size[1] # 第 n+1 层的维度
xavier_stddev = np.sqrt(2 / (in_dim + out_dim)) # 使用 xavier 对权重进行初始化
return tf.Variable(tf.truncated_normal([in_dim, out_dim], stddev=xavier_stddev), dtype=tf.float32)
# 定义神经网络
def neural_net(X, weights, biases):
num_layers = len(weights) + 1 # 神经网络层数
H = X
for l in range(0, num_layers - 2):
W = weights[l]
b = biases[l]
H = tf.sigmoid(tf.add(tf.matmul(H, W), b))
W = weights[-1]
b = biases[-1]
Y = tf.add(tf.matmul(H, W), b)
return Y
in_weights, in_biases = initialize_NN(layers)
def net(X):
h = neural_net(X, in_weights, in_biases)
return h
output = net(x_tf)
# loss
y_model = tf.nn.softmax(output)
loss = -tf.reduce_sum(y_tf * tf.log(y_model))
correct_prediction = tf.equal(tf.argmax(y_model, 1), tf.argmax(y_tf, 1))
accuracy = 0
# Optimization
# 10000 100 0.08
optimizer_GradientDescent = tf.train.GradientDescentOptimizer(speed)
train_op_Adam = optimizer_GradientDescent.minimize(loss)
# tf session
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
tf_dict = {x_tf: X_train, y_tf: train_label}
start_time = time.time()
for it in range(nIter):
sess.run(train_op_Adam, tf_dict)
# Print
if it % 1000 == 0:
elapsed = time.time() - start_time
loss_value = sess.run(loss, tf_dict)
print('It: %d, Loss: %.7e, Time: %.2f' % (it, loss_value, elapsed))
start_time = time.time()
for i in range(23):
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
XX = [[]]
XX[0] = X_test[i]
X = XX
Y = test_label[i]
a = sess.run(accuracy, feed_dict={x_tf: X, y_tf: Y})
if a==1:
print(i+1)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
accuracy = sess.run(accuracy, feed_dict={x_tf: X_test, y_tf: test_label})
print(accuracy)
一些图片












## 7、模拟B等级曲线
```c
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
Y2=[0 0.066799583 0.13505206 0.20658008 0.276812293 0.302883401 0.370215852 0.406296668 0.458295295 0.508718692 0.544408837 0.548493958 0.588765696 0.625764576 0.635605146 0.673527424 0.696925431 0.705315993 0.742936326 0.776400729 0.762022595 0.791503697 0.814998933 0.822297861 0.835301602 0.845747745 0.842070844 0.868159536 0.885864919];
Y3=[0 0.068725306 0.122099029 0.181252146 0.263302863 0.290189098 0.34971559 0.390771683 0.45723807 0.492660433 0.513660239 0.530248706 0.587762408 0.590097045 0.642993656 0.658839416 0.696870573 0.719103552 0.711101237 0.750627656 0.776816043 0.784480512 0.795566274 0.820051434 0.832288422 0.844089875 0.836974326 0.872558957 0.895164739];
A = -200:0.1:-190;
B = -10:0.1:-8;
C = 14:0.1:16;
D = -1:0.1:1;
E = [];
XA = [];
XC=[];
XB=[];
XD=[];
XX = [];
ii = 0;
e = 0;
for i=1:length(A)
a=A(i);
for j=1:length(B)
b=B(j);
for p=1:length(D)
d=D(p);
for k=1:length(C)
c=C(k);
e = 0;
for s=1:length(X)
x=X(s);
f = a*x^3+b*x^2+c*x+d;
e = e+(f-Y2(s))^2;
end
if e < 0.02255
ii = ii + 1;
XA(ii) =a;
XB(ii)=b;
XC(ii)=c;
XD(ii)=d;
XX(ii) = ii;
E(ii) = e;
end
end
end
end
end
[~,position]=min(E);
XA(position)
XB(position)
XC(position)
XD(position)
plot(XX, E);
8、模拟C等级曲线
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
Y2=[0 0.066799583 0.13505206 0.20658008 0.276812293 0.302883401 0.370215852 0.406296668 0.458295295 0.508718692 0.544408837 0.548493958 0.588765696 0.625764576 0.635605146 0.673527424 0.696925431 0.705315993 0.742936326 0.776400729 0.762022595 0.791503697 0.814998933 0.822297861 0.835301602 0.845747745 0.842070844 0.868159536 0.885864919];
Y3=[0 0.068725306 0.122099029 0.181252146 0.263302863 0.290189098 0.34971559 0.390771683 0.45723807 0.492660433 0.513660239 0.530248706 0.587762408 0.590097045 0.642993656 0.658839416 0.696870573 0.719103552 0.711101237 0.750627656 0.776816043 0.784480512 0.795566274 0.820051434 0.832288422 0.844089875 0.836974326 0.872558957 0.895164739];
A = -165:0.1:-160;
B = -15:0.1:-10;
C = 14:0.1:16;
D = -1:0.1:1;
E = [];
XA = [];
XC=[];
XB=[];
XD=[];
XX = [];
ii = 0;
e = 0;
for i=1:length(A)
a=A(i);
for j=1:length(B)
b=B(j);
for p=1:length(D)
d=D(p);
for k=1:length(C)
c=C(k);
e = 0;
for s=1:length(X)
x=X(s);
f = a*x^3+b*x^2+c*x+d;
e = e+(f-Y3(s))^2;
end
if e < 0.02255
ii = ii + 1;
XA(ii) =a;
XB(ii)=b;
XC(ii)=c;
XD(ii)=d;
XX(ii) = ii;
E(ii) = e;
end
end
end
end
end
[~,position]=min(E);
XA(position)
XB(position)
XC(position)
XD(position)
plot(XX, E);
09、信誉评级A客户流失率实际值与预测曲线
clear;
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y1=[0 0.094574126 0.135727183 0.224603354 0.302038102 0.347315668 0.41347177 0.447890973 0.497634453 0.511096612 0.573393087 0.609492115 0.652944774 0.667541843 0.694779921 0.708302023 0.731275401 0.775091405 0.798227368 0.790527266 0.815196986 0.814421029 0.854811097 0.870317343 0.871428085 0.885925945 0.874434682 0.902725909 0.922060687];
a=-194.7;
b=-13.4;
c=15.6;
d=-0.5;
for i=1:length(X)
x=X(i);
f = a*x^3+b*x^2+c*x+d;
F(i) = f;
end
plot(X, Y1, '*');
hold on;
plot(X, F, 'r','linewidth', 2);
axis([0.02 0.18 0 1]);
xlabel('贷款年利率');
ylabel('信誉评级A客户流失率');
title('信誉评级A客户流失率实际值与预测曲线');
legend('实际值' ,'预测曲线');
10、信誉评级B客户流失率实际值与预测曲线
clear;
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y2=[0 0.066799583 0.13505206 0.20658008 0.276812293 0.302883401 0.370215852 0.406296668 0.458295295 0.508718692 0.544408837 0.548493958 0.588765696 0.625764576 0.635605146 0.673527424 0.696925431 0.705315993 0.742936326 0.776400729 0.762022595 0.791503697 0.814998933 0.822297861 0.835301602 0.845747745 0.842070844 0.868159536 0.885864919];
a=-194.8;
b=-9.6;
c=14.8;
d=-0.5;
for i=1:length(X)
x=X(i);
f = a*x^3+b*x^2+c*x+d;
F(i) = f;
end
plot(X, Y2, '*');
hold on;
plot(X, F, 'r','linewidth', 2);
axis([0.02 0.18 0 1]);
xlabel('贷款年利率');
ylabel('信誉评级B客户流失率');
title('信誉评级B客户流失率实际值与预测曲线');
legend('实际值' ,'预测曲线');
11、信誉评级C客户流失率实际值与预测曲线
clear;
X = [0.04 0.0425 0.0465 0.0505 0.0545 0.0585 0.0625 0.0665 0.0705 0.0745 0.0785 0.0825 0.0865 0.0905 0.0945 0.0985 0.1025 0.1065 0.1105 0.1145 0.1185 0.1225 0.1265 0.1305 0.1345 0.1385 0.1425 0.1465 0.15
];
Y3=[0 0.068725306 0.122099029 0.181252146 0.263302863 0.290189098 0.34971559 0.390771683 0.45723807 0.492660433 0.513660239 0.530248706 0.587762408 0.590097045 0.642993656 0.658839416 0.696870573 0.719103552 0.711101237 0.750627656 0.776816043 0.784480512 0.795566274 0.820051434 0.832288422 0.844089875 0.836974326 0.872558957 0.895164739];
a=-159.7;
b=-14.5;
c=14.8;
d=-0.5;
F = [];
for i=1:length(X)
x=X(i);
f = a*x^3+b*x^2+c*x+d;
F(i) = f;
end
plot(X, Y3, '*');
hold on;
plot(X, F, 'r','linewidth', 2);
axis([0.02 0.18 0 1]);
xlabel('贷款年利率');
ylabel('信誉评级C客户流失率');
title('信誉评级C客户流失率实际值与预测曲线');
legend('实际值' ,'预测曲线');
12、求最优解
clear;
a1=-194.7;
b1=-13.4;
c1=15.6;
d1=-0.5;
a2=-194.8;
b2=-9.6;
c2=14.8;
d2=-0.5;
a3=-159.7;
b3=-14.5;
c3=14.8;
d3=-0.5;
% 代号-得分-等级
E_Z_DJ = [
1 0.1172 9
2 0.1173 9
12 0.5834 7
25 0.1163 7
34 0.1151 7
38 0.1841 7
45 0.1447 7
47 0.1157 7
49 0.1167 7
53 0.1155 7
56 0.1155 7
60 0.1579 7
61 0.2009 7
62 0.8322 7
63 0.1165 7
64 0.1061 5
66 0.113 5
69 0.3324 5
71 0.1166 7
73 0.1161 7
75 0.1152 7
76 0.1263 5
77 0.1157 7
78 0.1161 7
80 0.1138 5
82 0.1178 7
86 0.1148 7
87 0.1132 5
88 0.1146 5
89 0.1188 5
90 0.1156 7
91 0.1153 7
92 0.1142 5
93 0.1124 5
94 0.1058 5
95 0.1098 5
96 0.1111 5
98 0.1129 5
99 0.1138 7
100 0.1122 5
102 0.1164 7
103 0.1382 7
104 0.1662 7
105 0.1147 7
106 0.1156 7
107 0.1149 5
108 0.1128 5
109 0.1149 7
110 0.1129 5
111 0.1132 5
112 0.1134 5
113 0.1126 5
114 0.1111 5
115 0.1134 5
116 0.1125 5
117 0.1068 5
118 0.1134 5
119 0.1062 5
120 0.1134 5
121 0.1118 5
122 0.1126 5
123 0.1709 5
124 0.1128 5
125 0.1123 5
126 0.113 5
127 0.1123 5
128 0.1381 5
129 0.1127 5
130 0.112 5
131 0.1141 5
132 0.1126 5
133 0.1145 5
134 0.1124 5
135 0.113 5
136 0.1119 5
137 0.1127 5
138 0.1128 5
139 0.1134 5
140 0.112 5
141 0.1057 5
142 0.1118 5
143 0.1132 5
144 0.1136 5
145 0.1333 5
146 0.1126 5
147 0.1119 5
148 0.1115 5
149 0.1123 5
150 0.1148 5
151 0.1153 5
152 0.1117 5
153 0.1116 5
154 0.1129 5
155 0.1128 5
156 0.1127 5
157 0.1132 5
158 0.1129 5
159 0.1115 5
160 0.1132 5
161 0.1126 5
162 0.1118 5
163 0.1115 5
164 0.1119 5
165 0.1118 5
166 0.1133 5
167 0.1127 5
168 0.1113 5
169 0.1141 5
170 0.1133 5
171 0.1125 5
172 0.1118 5
173 0.1115 5
174 0.1124 5
175 0.1192 5
176 0.1126 5
177 0.1125 5
178 0.1128 5
179 0.1123 5
180 0.1129 5
181 0.1135 5
182 0.1127 5
183 0.1123 5
184 0.1123 5
185 0.1128 5
186 0.1116 5
187 0.1129 5
188 0.1122 5
189 0.1129 5
190 0.113 5
191 0.1121 5
192 0.1145 5
193 0.1125 5
194 0.1117 5
195 0.1127 5
196 0.1139 5
197 0.1127 5
198 0.1144 5
199 0.1128 5
200 0.1108 5
201 0.1118 5
202 0.1156 5
203 0.1127 5
204 0.1129 5
205 0.1123 5
206 0.5633 5
207 0.1166 5
208 0.1126 5
209 0.1132 5
210 0.1129 5
211 0.113 5
212 0.1123 5
213 0.1165 5
214 0.1155 5
215 0.1131 5
216 0.1133 5
217 0.1143 5
218 0.1134 5
219 0.1118 5
220 0.1545 5
221 0.1126 5
222 0.1124 5
223 0.1132 5
224 0.1152 5
225 0.1206 5
226 0.1151 5
227 0.1123 5
228 0.1125 5
229 0.1126 5
230 0.1117 5
231 0.1139 5
232 0.1574 5
233 0.1633 5
234 0.13 5
235 0.1844 5
236 0.134 5
237 0.2421 5
238 0.1118 5
239 0.1123 5
240 0.118 5
241 0.1132 5
242 0.1124 5
243 0.1138 5
244 0.1213 5
245 0.1107 5
246 0.1129 5
247 0.2526 5
248 0.1121 5
249 0.1134 5
250 0.1133 5
251 0.1351 5
252 0.2107 5
253 0.1157 5
254 0.1305 5
255 0.112 5
256 0.1105 5
257 0.1711 5
258 0.1115 5
259 0.1821 5
260 0.1164 5
261 0.112 5
262 0.1086 5
263 0.1119 5
264 0.1198 5
265 0.1219 5
266 0.1186 5
267 0.1138 5
268 0.1562 5
269 0.114 5
270 0.1426 5
271 0.1075 5
272 0.1107 5
273 0.1123 5
274 0.1166 5
275 0.1139 5
276 0.1128 5
277 0.1208 5
278 0.1101 5
279 0.1121 5
280 0.1127 5
281 0.1109 5
282 0.1103 5
283 0.1122 5
284 0.1109 5
285 0.1121 5
286 0.1154 5
287 0.1149 5
288 0.1122 5
289 0.1139 5
290 0.1139 5
291 0.1124 5
292 0.2104 5
293 0.1129 5
294 0.1135 5
295 0.1126 5
296 0.1133 5
297 0.113 5
298 0.1139 5
299 0.1153 5
300 0.1122 5
301 0.1179 5
302 0.1098 5
];
E = E_Z_DJ(:, 1);
DJ = E_Z_DJ(:, 3);
Z = E_Z_DJ(:, 2);
fun_range = [0,3.08;0,2.1]; %每个维度的求解范围,行代表维度,第一列最小值,第二列最大值
density = 0.01; %图像中取点的密度
d = 2; %维度
popsize = 10; %种群大小
maxgen = 100; %最大迭代次数
limit_v = 10; %最大运动速度
maxormin = 0; %求最大值还是最小值。最大值为1,最小值为0
dynamic = 1; %是否采用动态参数
W = [0.7,1.4]; %惯性因子
C2 = [0.5,2.5];
C1 = [0.5,2.5]; %学习因子。
ZZ = pso1_im(funct,fun_range,density,d);
[x,v,fitness,pbest,gbest,gbest_fitness,gbest_index,pbest_fitness] =...
pso1_in(funct,popsize,d,fun_range,limit_v,maxormin);
[gbest_fitness,gbest_index,record] =...
pso1_in2(funct,d,popsize,maxgen,dynamic,W,C1,C2,fun_range,limit_v,density...
,x,v,fitness,pbest,gbest,gbest_fitness,gbest_index,pbest_fitness,maxormin);
% sigma = 4:1:15; 年利率
% D = 10:1:100; % 投放金额
T = 1; %周期为 1 年
M = 10000; % 总贷款额度1亿
Sigma = [];
DD = [];
Beta = [];
W = []; % 利润,即最大化目标
Z_S = ones(1, length(E)); % 每个利率 1不用管
Z_D = ones(1, length(E)); % 每个投资
N = 10000; % 迭代次数
nnn = 0;
for i=1:1:N
Sigma = []; % 该次遍历的利率
DD = []; % 该次遍历的贷款
w = 0; % 该次遍历的目标值
for j=1:length(E)
Sigma(j) = 0.04 + (0.15-0.04).*rand(1,1);
x = Sigma(j);
DD(j) = 10 + (100-10).*rand(1,1);
d = DD(j);
if DJ(j) == 1
Beta(j) = a1*x^3+b1*x^2+c1*x+d1;
elseif DJ(j) == 2
Beta(j) = a2*x^3+b2*x^2+c2*x+d2;
else
Beta(j) = a3*x^3+b3*x^2+c3*x+d3;
end
w = w + d*x*(1-Beta(j))*Z(j);
end
if w > 60
nnn = nnn+1;
W(nnn) = w;
Z_S(nnn,:) = Sigma(:);
Z_D(nnn,:) = DD(:);
end
end
XX = 1:1:nnn;
plot(XX, W, '*');
for i=1:length(Z_S(:, 1))
sum(Z_D(i,:))
end
13、神经网络
import numpy as np
import pandas as pd
import time
import tensorflow.compat.v1 as tf # 本行报错不用处理
tf.disable_v2_behavior()
# 图网络 和 生成对抗网络
IN_DIV = 24 # 输入维度
OUT_DIV = 4 # 输出维度
nIter = 10000 # 迭代次数为 10000 次
speed = 0.08
N = 100 # 每层神经元个数
NATrain = 25 # 每一类的训练样本数
NBTrain = 25
NCTrain = 30
NDTrain = 20
NATest = 2 # 每一类的测试样本数
NBTest = 13
NCTest = 4
NDTest = 4
# 数据集导入
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
train = np.array(train)
test = np.array(test)
def noramlization(data):
minVals = data.min(0)
maxVals = data.max(0)
ranges = maxVals - minVals
normData = np.zeros(np.shape(data))
m = data.shape[0]
normData = data - np.tile(minVals, (m, 1))
normData = normData/np.tile(ranges, (m, 1))
return normData, ranges, minVals
A_train = train[0:NATrain, :]
B_train = train[NATrain:NATrain+NBTrain, :]
C_train = train[NATrain+NBTrain:NATrain+NBTrain+NCTrain, :]
D_train = train[NATrain+NBTrain+NCTrain:, :]
A_test = test[0:NATest, :]
B_test = test[NATest:NATest+NBTest, :]
C_test = test[NATest+NBTest:NATest+NBTest+NCTest, :]
D_test = test[NATest+NBTest+NCTest:, :]
# 数据格式化
X_train = np.vstack((A_train, B_train, C_train, D_train))
X_test = np.vstack((A_test, B_test, C_test, D_test))
train_label = np.matrix([[1, 0, 0, 0]] * NATrain + [[0, 1, 0, 0]] * NBTrain + [[0, 0, 1, 0]] * NCTrain + \
[[0, 0, 0, 1]] * NDTrain)
test_label = np.matrix([[1, 0, 0, 0]] * NATest + [[0, 1, 0, 0]] * NBTest + [[0, 0, 1, 0]] * NCTest + \
[[0, 0, 0, 1]] * NDTest)
print(test_label)
'''
我们采用三层前向神经网络来优化这个任务, 其中每层的神经元个数取20,
初始化取 xavier initialization,优化处理器取 GradientDescentOptimizer,
学习率取 0.001, 激活函数选取 sigmoid 函数, 迭代次数为 1000.
'''
layers = [IN_DIV, N, N, N, OUT_DIV] # 输入层 2 个维度,中间层为 3 层,每层 20 个神经元,输出层维度为 5,因为要分为 5 类
# define neural network structure
# tf.palceholder
x_tf = tf.placeholder(tf.float32, shape=[None, X_train.shape[1]])
y_tf = tf.placeholder(tf.float32, shape=[None, train_label.shape[1]])
def initialize_NN(layers):
weights = [] # 权重矩阵
biases = [] # 截距矩阵 Y = W*X + b
num_layers = len(layers)
for l in range(0, num_layers - 1):
W = xavier_init(size=[layers[l], layers[l + 1]])
b = tf.Variable(tf.zeros([1, layers[l + 1]], dtype=tf.float32), dtype=tf.float32)
weights.append(W)
biases.append(b)
return weights, biases
def xavier_init(size):
in_dim = size[0] # 第 n 层的维度
out_dim = size[1] # 第 n+1 层的维度
xavier_stddev = np.sqrt(2 / (in_dim + out_dim)) # 使用 xavier 对权重进行初始化
return tf.Variable(tf.truncated_normal([in_dim, out_dim], stddev=xavier_stddev), dtype=tf.float32)
# 定义神经网络
def neural_net(X, weights, biases):
num_layers = len(weights) + 1 # 神经网络层数
H = X
for l in range(0, num_layers - 2):
W = weights[l]
b = biases[l]
H = tf.sigmoid(tf.add(tf.matmul(H, W), b))
W = weights[-1]
b = biases[-1]
Y = tf.add(tf.matmul(H, W), b)
return Y
in_weights, in_biases = initialize_NN(layers)
def net(X):
h = neural_net(X, in_weights, in_biases)
return h
output = net(x_tf)
# loss
y_model = tf.nn.softmax(output)
loss = -tf.reduce_sum(y_tf * tf.log(y_model))
correct_prediction = tf.equal(tf.argmax(y_model, 1), tf.argmax(y_tf, 1))
accuracy = 0
# Optimization
# 10000 100 0.08
optimizer_GradientDescent = tf.train.GradientDescentOptimizer(speed)
train_op_Adam = optimizer_GradientDescent.minimize(loss)
# tf session
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
tf_dict = {x_tf: X_train, y_tf: train_label}
start_time = time.time()
for it in range(nIter):
sess.run(train_op_Adam, tf_dict)
# Print
if it % 1000 == 0:
elapsed = time.time() - start_time
loss_value = sess.run(loss, tf_dict)
print('It: %d, Loss: %.7e, Time: %.2f' % (it, loss_value, elapsed))
start_time = time.time()
for i in range(23):
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
XX = [[]]
XX[0] = X_test[i]
X = XX
Y = test_label[i]
a = sess.run(accuracy, feed_dict={x_tf: X, y_tf: Y})
if a==1:
print(i+1)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
accuracy = sess.run(accuracy, feed_dict={x_tf: X_test, y_tf: test_label})
print(accuracy)
一些图片












文章来源地址https://www.toymoban.com/news/detail-651526.html
文章来源:https://www.toymoban.com/news/detail-651526.html
到了这里,关于2020年高教社杯全国大学生数学建模C题中小微企业信贷决策(Matlab代码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!