本文研究通过C语言实现最小二乘法拟合直线。
1 引入
最小二乘法,简单来说就是根据一组观测得到的数值,寻找一个函数,使得函数与观测点的误差的平方和达到最小。在工程实践中,这个函数通常是比较简单的,例如一次函数或二次函数。
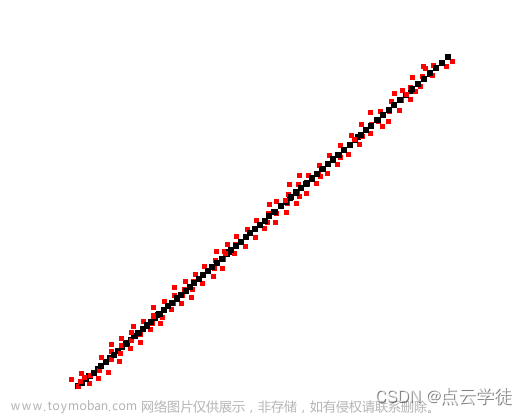
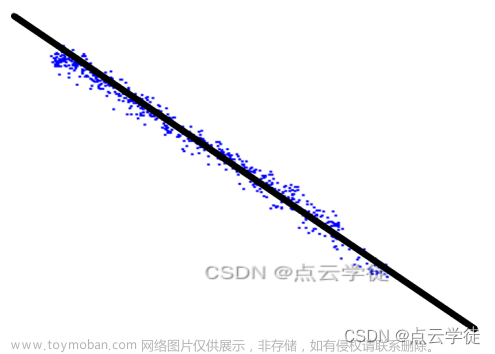
汽车上的毫米波雷达可以探测到其他目标车辆,通过最小二乘法拟合目标车辆历史点,可以简单地预测目标汽车未来的走向。
后文会推导最小二乘法拟合直线,并通过C语言实现,最后进行简单的验证。对于二次及更高次多项式的拟合,采用类似的方法。
2 公式推导
作为工程应用,推导公式不需要像数学上的那么抽象,只需要针对当前需求推导即可。
首先,需要拟合的方程为一次函数:
y = a x + b y = ax + b y=ax+b
并且已知n个观测点:
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
(
x
n
,
y
n
)
(x_{1}, y_{1}),(x_{2}, y_{2}),...(x_{n}, y_{n})
(x1,y1),(x2,y2),...(xn,yn)
则拟合的误差的平方和为:
E
(
a
,
b
)
=
∑
i
=
1
n
(
a
x
i
+
b
−
y
i
)
2
E(a,b)=\sum_{i=1}^n\left({{}}a{{x}}{}_{{i}}+b-{{y}}{}_{{i}}\right)^2
E(a,b)=i=1∑n(axi+b−yi)2
注意,x和y是已知量,该函数是关于a和b的二元函数。目标是求误差的最小值,因此需要分别对a和b求偏导数:
∂
E
∂
a
=
∑
i
=
1
n
2
⋅
(
a
x
i
+
b
−
y
i
)
⋅
x
i
=
2
∑
i
=
1
n
(
a
x
i
2
+
b
x
i
−
y
i
x
i
)
\frac{\partial E}{\partial a}=\sum_{i=1}^n{2\cdot\left(a{{x}}{}_{{i}}+b-{{y}}{}_{{i}}\right)}\cdot{{x}}{}_{{i}}=2\sum_{i=1}^n{\left(a{{x}}_{{i}}^{{2}}+b{{x}}{}_{{i}}-{{y}}{}_{{i}}{{x}}{}_{{i}}\right)}
∂a∂E=i=1∑n2⋅(axi+b−yi)⋅xi=2i=1∑n(axi2+bxi−yixi)
∂
E
∂
b
=
∑
i
=
1
n
2
⋅
(
a
x
i
+
b
−
y
i
)
=
2
∑
i
=
1
n
(
a
x
i
+
b
−
y
i
)
\:\frac{\partial E}{\partial b}=\sum_{i=1}^n{2\cdot\left(a{{x}}{}_{{i}}+b-{{y}}{}_{{i}}\right)}=2\sum_{i=1}^n\left(a{{x}}{}_{{i}}+b-{{y}}{}_{{i}}\right)
∂b∂E=i=1∑n2⋅(axi+b−yi)=2i=1∑n(axi+b−yi)
对偏导数取值为0,可以得到线性方程组:
a
∑
i
=
1
n
x
i
2
+
b
∑
i
=
1
n
x
i
=
∑
i
=
1
n
y
i
x
i
a\sum_{i=1}^n{{{x}}_{{i}}^{{2}}}\:+b\sum_{i=1}^n{{x}}{}_{{i}}\:=\sum_{i=1}^n{{y}}{}_{{i}}{{x}}{}_{{i}}
ai=1∑nxi2+bi=1∑nxi=i=1∑nyixi
a
∑
i
=
1
n
x
i
+
b
n
=
∑
i
=
1
n
y
i
a\sum_{i=1}^n{{x}}{}_{{i}}\:+\:bn_{{}}\:=\sum_{i=1}^n{{y}}{}_{{i}}{{}}
ai=1∑nxi+bn=i=1∑nyi
求解方程组可以用克拉默法则:
D
=
∣
∑
i
=
1
n
x
i
2
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
n
∣
=
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
D=\:\left|\begin{matrix}{\sum_{i=1}^n{{{x}}_{{i}}^{{2}}}{}} & {\sum_{i=1}^n{{{x}}_{{i}}^{{}}}{}} \\ {\sum_{i=1}^n{{{x}}_{{i}}^{{}}}{}} & n\end{matrix}\right|\:=\:n\sum_{i=1}^n{{x}}_{{i}}^{{2}}\:-\:\left(\sum_{i=1}^n{{x}}_{{i}}^{}\right)^2
D=
∑i=1nxi2∑i=1nxi∑i=1nxin
=ni=1∑nxi2−(i=1∑nxi)2
D
a
=
∣
∑
i
=
1
n
x
i
y
i
∑
i
=
1
n
x
i
∑
i
=
1
n
y
i
n
∣
=
n
∑
i
=
1
n
x
i
y
i
−
∑
i
=
1
n
x
i
∑
i
=
1
n
y
i
{{D}}{}_{{a}}=\:\left|\begin{matrix}{\sum_{i=1}^n{{{{x{}}{}_{{i}}y}}_{{i}}}{}} & {\sum_{i=1}^n{{{x}}_{{i}}^{{}}}{}} \\ {\sum_{i=1}^n{{y{}}_{{i}}^{{}}}{}} & n\end{matrix}\right|\:=\:n\sum_{i=1}^n{{{x{}}{}_{{i}}y}}_{{i}}^{{}}\:-\:\sum_{i=1}^n{x{}}{}_{{i}}\sum_{i=1}^n{y{}}_{{i}}^{{}}
Da=
∑i=1nxiyi∑i=1nyi∑i=1nxin
=ni=1∑nxiyi−i=1∑nxii=1∑nyi
D
b
=
∣
∑
i
=
1
n
x
i
2
∑
i
=
1
n
x
i
y
i
∑
i
=
1
n
x
i
∑
i
=
1
n
y
i
∣
=
∑
i
=
1
n
x
i
2
∑
i
=
1
n
y
i
−
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
y
i
{{D}}{}_{{b}}=\:\left|\begin{matrix}{\sum_{i=1}^n{{{x}}_{{i}}^{{2}}}{}} & {\sum_{i=1}^n{{{{x{}}{}_{{i}}y}}_{{i}}^{{}}}{}} \\ {\sum_{i=1}^n{{{x}}_{{i}}^{{}}}{}} & \sum_{i=1}^n{{y}}{}_{{i}}\end{matrix}\right|\:=\:\sum_{i=1}^n{{x}}_{{i}}^{{2}}\:\sum_{i=1}^n{{y}}{}_{{i}}\:-\:\sum_{i=1}^n{{x}}_{{i}}^{{}}\sum_{i=1}^n{{{x{}}{}_{{i}}{y{}}{}_{{i}}}}
Db=
∑i=1nxi2∑i=1nxi∑i=1nxiyi∑i=1nyi
=i=1∑nxi2i=1∑nyi−i=1∑nxii=1∑nxiyi
可以求得a和b:
a
=
D
a
D
=
n
∑
x
i
y
i
−
∑
x
i
∑
y
i
n
∑
x
i
2
−
(
∑
x
i
)
2
a\:=\:\frac{{{D}}{}_{{a}}}{D}\:=\:\frac{n\sum{{{x}}{}_{{i}}}{{y}}{}_{{i}}-\sum{{{x}}{}_{{i}}}\sum{{y{}}{}_{{i}}}}{n\sum{{x}}_{{i}}^{{2}}-\left(\sum{{x}}{}_{{i}}\right)^2}
a=DDa=n∑xi2−(∑xi)2n∑xiyi−∑xi∑yi
b
=
D
b
D
=
∑
x
i
2
∑
y
i
−
∑
x
i
∑
x
i
y
i
n
∑
x
i
2
−
(
∑
x
i
)
2
b\:=\:\frac{{{D}}{}_{b{}}}{D}\:=\:\frac{\sum{{x}}_{{i}}^{{2}}{{}}{}_{{}}\sum{{y{}}{}_{{i}}}-\sum{{{x}}{}_{{i}}}\sum{{{{x}}{}_{{i}}y{}}{}_{{i}}}}{n\sum{{x}}_{{i}}^{{2}}-\left(\sum{{x}}{}_{{i}}\right)^2}
b=DDb=n∑xi2−(∑xi)2∑xi2∑yi−∑xi∑xiyi
3 C语言代码实现
1)首先设计头文件polyfit_types.h,用于定义一些基本类型和结构体;
//polyfit_types.h
#ifndef POLYFIT_TYPES_H
#define POLYFIT_TYPES_H
typedef signed char int8;
typedef unsigned char uint8;
typedef short int16;
typedef unsigned short uint16;
typedef int int32;
typedef unsigned int uint32;
typedef float float32;
typedef struct POINT_TAG
{
float32 x_f32;
float32 y_f32;
}POINT_TYPE;
typedef struct LINE_TAG
{
float32 a_f32;
float32 b_f32;
}LINE_TYPE;
#endif
这里先定义一些基本类型,比如uint8,float32等。接着定义两个结构体:点和直线。点结构体的成员是点的x和y坐标,直线结构体的成员是直线的系数a和b。
2)设计头文件polyfit.h;
//polyfit.h
#ifndef POLYFIT_H
#define POLYFIT_H
//Include
#include "polyfit_types.h"
//Define
#define EPS 0.000001F
#define OK 1U
#define NOK 0U
//Function
uint8 polyfit(const POINT_TYPE* points_vs, const uint8 point_number_u8, LINE_TYPE* line_s, float32* square_error_f32);
#endif
头文件首先包含了type头文件。接着是宏定义EPS表示一个极小值,用于浮点数相等比较。然后就是函数polyfit的声明,函数的前两个参数是输入的点的数组和点的数量,后两个参数表示输出的直线和残差的平方和。
3)设计C文件polyfit.c,是实现算法的核心代码;
//polyfit.c
#include <math.h>
#include <string.h>
#include "polyfit.h"
//Function
uint8 polyfit(const POINT_TYPE* points_vs, const uint8 point_number_u8, LINE_TYPE* line_s, float32* square_error_f32)
{
//var
float32 sum_x_f32 = 0.0F;
float32 sum_xy_f32 = 0.0F;
float32 sum_x2_f32 = 0.0F;
float32 sum_y_f32 = 0.0F;
float32 xi = 0.0F;
float32 yi = 0.0F;
float32 Det_f32 = 0.0F;
float32 Det_a_f32 = 0.0F;
float32 Det_b_f32 = 0.0F;
float32 Err = 0.0F;
uint8 index_u8;
//initialize
*square_error_f32 = 0.0F;
memset(line_s, 0.0F, sizeof(LINE_TYPE));
//calculate sum
for (index_u8 = 0U; index_u8 < point_number_u8; index_u8++)
{
xi = points_vs[index_u8].x_f32;
yi = points_vs[index_u8].y_f32;
sum_x_f32 += xi;
sum_xy_f32 += xi * yi;
sum_x2_f32 += xi * xi;
sum_y_f32 += yi;
}
//calculate determinant
Det_f32 = point_number_u8 * sum_x2_f32 - sum_x_f32 * sum_x_f32;
Det_a_f32 = point_number_u8 * sum_xy_f32 - sum_x_f32 * sum_y_f32;
Det_b_f32 = sum_x2_f32 * sum_y_f32 - sum_x_f32 * sum_xy_f32;
//determine if Det_f32 is 0
if (fabsf(Det_f32) < EPS)
{
return NOK;
}
//calculate coefficient
line_s->a_f32 = Det_a_f32 / Det_f32;
line_s->b_f32 = Det_b_f32 / Det_f32;
//calculate sum of square error
for (index_u8 = 0U; index_u8 < point_number_u8; index_u8++)
{
xi = points_vs[index_u8].x_f32;
yi = points_vs[index_u8].y_f32;
Err = yi - (line_s->a_f32 * xi + line_s->b_f32);
*square_error_f32 += Err * Err;
}
return OK;
}
代码中,首先定义局部变量,并初始化输出参数。接着,按照公式计算三个行列式,并判断D是否为0,如果为零就停止计算并返回。最后通过克拉默法则计算系数,以及根据算出的直线计算残差的平方和。
4 测试验证
在主函数里可以简单写一段测试代码,验证一下是否正确。
1)参考某百科,假设输入4个点为(1,6),(2,5),(3,7),(4,10),测试代码如下;
#include <stdio.h>
#include "polyfit.h"
int main()
{
POINT_TYPE point_vs[4];
point_vs[0].x_f32 = 1.0F; point_vs[0].y_f32 = 6.0F;
point_vs[1].x_f32 = 2.0F; point_vs[1].y_f32 = 5.0F;
point_vs[2].x_f32 = 3.0F; point_vs[2].y_f32 = 7.0F;
point_vs[3].x_f32 = 4.0F; point_vs[3].y_f32 = 10.0F;
LINE_TYPE line_s;
float32 square_error_f32;
uint8 retVal;
retVal = polyfit(point_vs, 4U, &line_s, &square_error_f32);
printf("retVal = %d , a = %f , b = %f , err = %f \r\n", retVal, line_s.a_f32, line_s.b_f32, square_error_f32);
}
打印出来的结果为:

这表示拟合的直线方程为:
y = 1.4 x + 3.5 y = 1.4x + 3.5 y=1.4x+3.5
绘图出来的结果是:
2)如果输入的4个点是(1,6),(1,5),(1,7),(1,10),即四个点在一条垂直于x轴的直线上,这时行列式D=0,就无法得出拟合结果:
#include <stdio.h>
#include "polyfit.h"
int main()
{
POINT_TYPE point_vs[4];
point_vs[0].x_f32 = 1.0F; point_vs[0].y_f32 = 6.0F;
point_vs[1].x_f32 = 1.0F; point_vs[1].y_f32 = 5.0F;
point_vs[2].x_f32 = 1.0F; point_vs[2].y_f32 = 7.0F;
point_vs[3].x_f32 = 1.0F; point_vs[3].y_f32 = 10.0F;
LINE_TYPE line_s;
float32 square_error_f32;
uint8 retVal;
retVal = polyfit(point_vs, 4U, &line_s, &square_error_f32);
printf("a = %f , b = %f , err = %f \r\n", line_s.a_f32, line_s.b_f32, square_error_f32);
}
打印出来的结果为:

5 总结
本文本文研究通过C语言实现最小二乘法拟合直线。在工程应用中,一次和二次多项式的拟合用的比较多。二次多项式拟合可以参考一次的推导过程和编程过程,需要求解三阶行列式求解三个系数。文章来源:https://www.toymoban.com/news/detail-651888.html
>>返回个人博客总目录文章来源地址https://www.toymoban.com/news/detail-651888.html
到了这里,关于C语言编程:最小二乘法拟合直线的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!