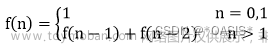递归
程序调用自身的编程技巧称为递归( recursion)
递归有两个过程,简单地说一个是递的过程,一个是归的过程。
递归的两个必要条件
1.存在限制条件,当满足这个限制条件的时候,递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件
.
递归本质就是函数调用,是函数调用,本质就要形成和释放栈帧,调用函数是有成本的,这个成本就体现在形成和释放栈帧上:时间+空间.递归就是不断形成栈帧的过程
通过上述我们也能了解到递归的一些限制
- 内存和CPU的资源是有限的,也就决定了,合理的递归是绝对不能无限递归下去
- 递归不是什么时候都能用,而是要满足自身的应用场景,即:目标问题的子问题,也可以采用相同的算法解决,本质就是分治的思想
- 核心思想:大事化小+递归出口
斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……
在讲解递归斐波那契数列之前,我们需要明白递归的本质
通过如上定义,我们可以定义讲用代码去实现斐波那契数列
首先来看递归版本的代码
递归版
int Fib(int n)
{
if(n<=0)
{
return 0;
}
else if (1 == n || 2 == n)
{
return 1;
}
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 5;
int x = Fib(n);
printf("fib(%d): %d\n", n, x);
return 0;
}
 这就是上式当n=5,即Fib(5)所形成的递归调用理论图
这就是上式当n=5,即Fib(5)所形成的递归调用理论图
而上述提到递归的本质是函数调用,由此可见,当n的值越大时(即所求的斐波那契数越大),调用的函数就越来越多,所以我们在此的时间成本和空间成本都非常之高
(时间复杂度为O(2^N),空间复杂度为O(N)).
通过如下代码可以证明
int main()
{
int n = 10; //n从40开始,时间就会慢慢增大得明显
//使用win提供的GetTickCount()函数,来获取开机到现在的累计时间(单位毫秒)
double start = GetTickCount();
int x = Fib(n);
double end = GetTickCount();
printf("%lf ms\n", (end - start));//二者进行相减就可以算出递归所用时间
system("pause");
return 0;
}
n从40开始时,时间就会明显变大,此时n即使每次只加1来测试时间,时间就会变大很多,这是因为从上面得递归调用理论图也可以看出,当F(4)变为F(5)的时候,F(4)分支下的F(3)及后面一系列都将出现在F(5)的另一边分支上,由此可见当F(40)变为F(41)时,F(39)及其一系列将会出现在F(41)的另一端分支上,所以即使每次只加1,变化也是巨大的
接下来我们采用迭代的思想来进行时间和空间上效率的提升(说直白点迭代就是循环)
迭代版
int Fib(int n)
{
int *dp = (int*)malloc(sizeof(int)*(n+1)); //多加一个是为了下标保持一致方便计算
//[0]不用(当然,也可以用,不过这里我们从1开始,为了后续方便)
dp[1] = 1;
dp[2] = 1;
int i = 3;
while(i<=n)
{
dp[i] = dp[i - 1] + dp[i - 2];
i++;
}
int ret = dp[n];
free(dp);
return ret;
}
其实这也算一种动态规划的算法,但是我们也能看出一些弊端,即我们将从第1位到第n位斐波那契数列都保存在了我们malloc出来的堆空间里面(空间复杂度时O(n)),然而任何一个斐波那契数都只与前面两个数有关,所以我们可以进行更近一步的优化
加强迭代版
int Fib(int n)
{
int first = 1;
int second = 1;
int third = 1;
while (n > 2){
third = second + first;
first = second;
second = third;
n--;
}
return third;
}
这个迭代版本的代码完美在时间和空间复杂度上都进行了极大的优化
总结
综上,我们也可以通过斐波那契的例子看出递归算法的在效率上一般不是很高,而迭代在效率上要高于递归.但是递归相对而言代码要比迭代简单一点,代码的可读性较强
递归运用较多的场景在于:
1.当问题和子问题具有递推关系(阶乘)。
1.具有递归性质的数据结构(链表、树)。文章来源:https://www.toymoban.com/news/detail-652716.html
因此递归函数也只是一种解决问题的技巧,它和其它技巧一样,也存在某些缺陷,具体来说就是:递归函数的时间开销和内存开销都非常大,甚至在极端情况下会导致程序崩溃(所以递归函数一定递了之后要归,不然最终会造成栈溢出)。所以我们在今后使用递归时,也要时刻考虑这一点文章来源地址https://www.toymoban.com/news/detail-652716.html
到了这里,关于递归以及斐波那契数列递归算法和迭代算法的实现与分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!