更快的求最近公共祖先（LCA）的算法-倍增法求LCA-Toy模板网

这篇具有很好参考价值的文章主要介绍了更快的求最近公共祖先（LCA）的算法-倍增法求LCA。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

leetcode 题目

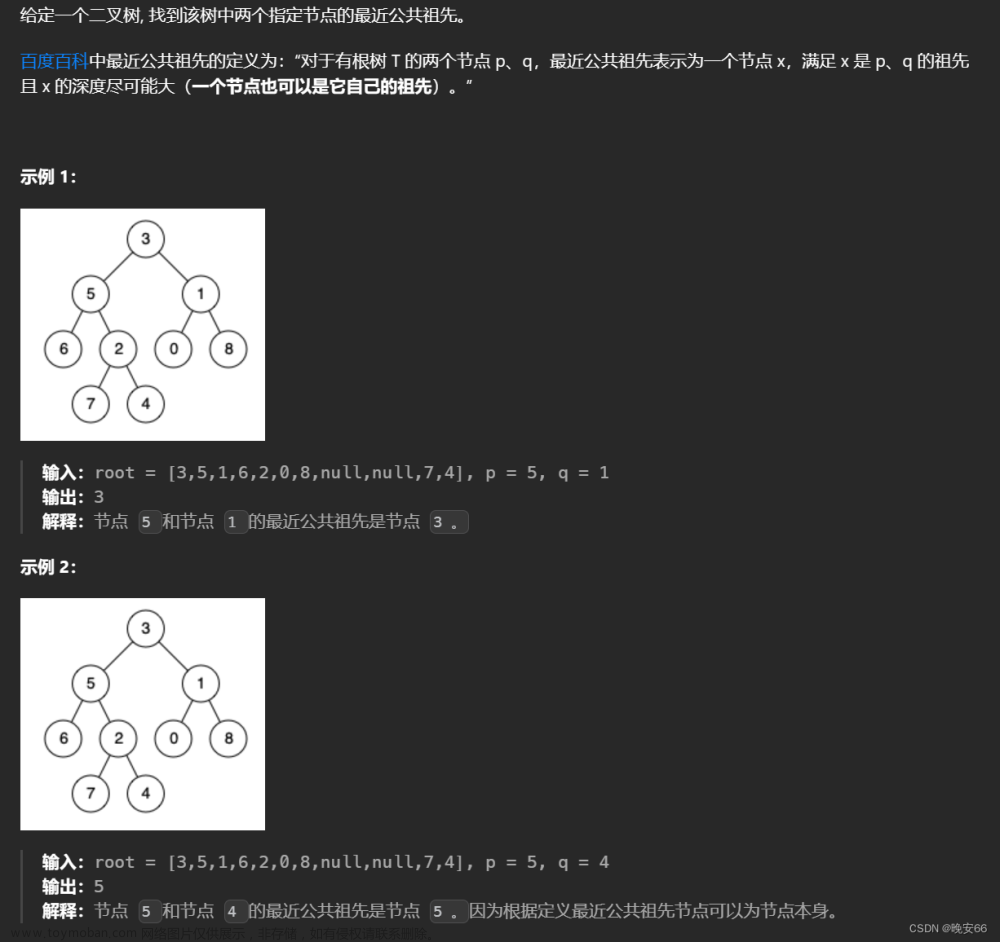
236. 二叉树的最近公共祖先

参考：最近公共祖先

思路

$\rm{fa}[i][j]$ 表示结点 $i$ 的第 $2^i$ 个组先
$\rm{dep}[i]$ 表示结点 $i$ 的深度
$\rm{next}[i][0]$ 表示结点 $i$ 的左子结点
$\rm{next}[i][1]$ 表示结点 $i$ 的右子结点

特别地,

i = 0 表示一个不存在的结点
i = 1 表示树的根结点
fa[i][0] 表示结点i的父节点

首先，通过树的深度优先遍历，计算fa和dep数组。
假定要求x和y两个结点的最近公共祖先，那么通过fa快速把x,y调整到一样的高度。然后分两种情况：

如果此时x = y, 则已经找到最近公共祖先
否则，通过fa找到最近公共祖先之下，第一个不是它们祖先的点。它们的父节点即是最近公共祖先。

复杂度分析

假设有n个结点
预处理：每个节点至多有 $\log n$ 个父节点，因此时间复杂度为 $\cdot \log n)$
查找：从上到下调平以从下到上找第一个共公祖先，最多 $O(\log n)$ 次，因此时间复杂度为 $T(n)=O(\log n)$ 。文章来源地址https://www.toymoban.com/news/detail-653418.html

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int[][] fa;
    int[] dep; 
    int[][] next;

    public void dfs(int node, int p){
        if(node != 0){
            fa[node][0] = p;
            dep[node] = dep[p] + 1;
            for(int i = 1; i < 31; i++){
                fa[node][i] = fa[fa[node][i-1]][i-1];
            }
            dfs(next[node][0], node);
            dfs(next[node][1], node);
        } 
    }

    public int lca(int x, int y){
        if(dep[x] > dep[y]) {
            int t = x; x = y; y = t;
        }
        int tmp = dep[y] - dep[x];
        int weight = 0;
        // 从下往上把两者高度调成一样
        while(tmp > 0){
            if((tmp & 1) == 1){
                y = fa[y][weight];
            }
            tmp >>= 1;
            weight ++;
        }
        // 如果相等，则已经找到答案
        if(x == y) return x;
        // 从上往下找到第一个非公共的
        for(int i = 30; i >= 0 && x != y; i--){
            if(fa[x][i] != fa[y][i]){
                x = fa[x][i];
                y = fa[y][i];
            }
        }
        return fa[x][0];
    }


    HashMap<TreeNode, Integer> map = new HashMap<>();
    ArrayList<TreeNode> arr = new ArrayList<>();
    int index = 0;
    public void proceed(TreeNode root){
        if(root != null){
            map.put(root, ++index);
            arr.add(root);
            proceed(root.left);
            proceed(root.right);
        }
    }

    public void proceed2(TreeNode root){
        if(root != null){
            next[map.get(root)][0] = map.get(root.left);
            next[map.get(root)][1] = map.get(root.right);
            proceed2(root.left);
            proceed2(root.right);
        }
    }

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        map.put(null, 0);
        arr.add(null);
        proceed(root);
        fa = new int[arr.size()][31];
        dep = new int[arr.size()];
        next = new int[arr.size()][2];
        proceed2(root);
        dfs(1, 0);
        return arr.get(lca(map.get(p), map.get(q)));
    }
}