【C++】矩阵的乘法-Toy模板网

这篇具有很好参考价值的文章主要介绍了【C++】矩阵的乘法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

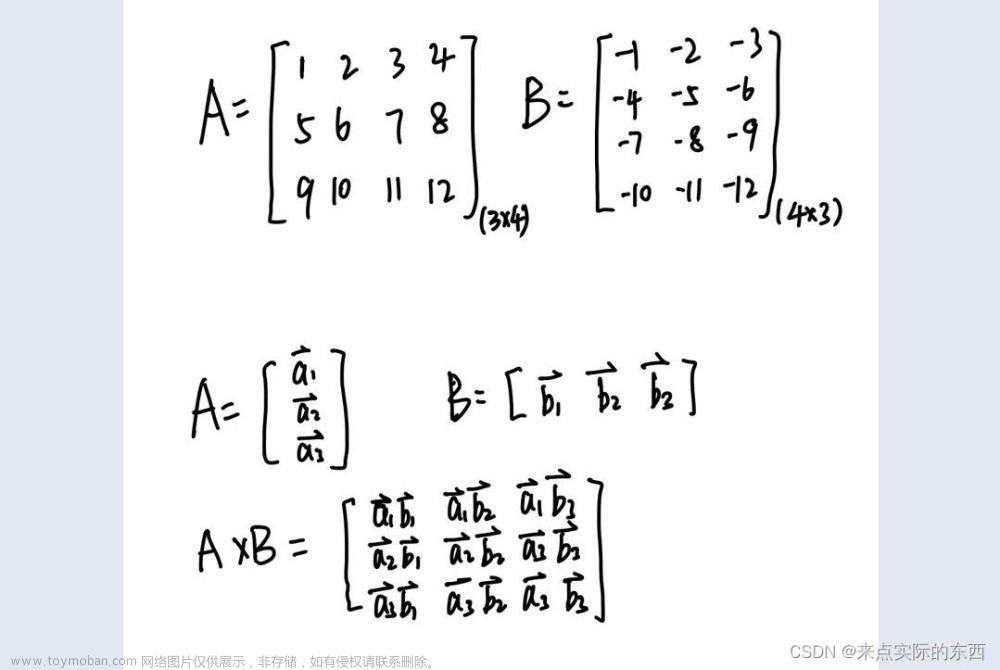
先复习一下矩阵的乘法。

已知

c++矩阵相乘,# 数学与编程,矩阵,c++,线性代数

求AB。

因为矩阵A是2×3矩阵，矩阵B是3×3矩阵，A的列数等于B的行数，所以矩阵A与B可以相乘，乘积AB是一个2×3矩阵。

c++矩阵相乘,# 数学与编程,矩阵,c++,线性代数

矩阵相乘时需要注意两点，一点是矩阵1的列数要等与矩阵2的行数，一点是矩阵相乘后的矩阵

c[i][j] = a[i][k]*b[k][j]

由矩阵相乘的性质可以用三层循环求出结果，注意i的循环需要放在最外层，j的循环需要放在中间层，k的循环需要放在最低层。

for(int i=0;i<ROW1;i++)
           for(int j=0;j<COL2;j++)
               for(int k=0;k<COL1;k++)
                   arr3[i][j] += arr1[i][k]*arr2[k][j];

完整代码：

#include<iostream>
using namespace std;

//第i个矩阵的行数和列数 
#define ROW1 3
#define COL1 3
#define ROW2 3
#define COL2 3

/*
矩阵乘法 
*/
void matrix_mutiplicate(double(*arr1)[COL1], double (*arr2)[COL2], double(*arr3)[COL2]) {
	if(COL1==ROW2) {
		//矩阵相乘的性质c[i][j] += a[i][k]*b[k][j] 
		for(int i=0;i<ROW1;i++)
			for(int j=0;j<COL2;j++)
				for(int k=0;k<COL1;k++)
					//	*(* (arr3 + i)+j) += *(*(arr1 + i) + k) * *(*(arr2 +k) + j);
					arr3[i][j] += arr1[i][k]*arr2[k][j];
	}
	return;
}


/*
打印矩阵 
*/
void matrix_print(double(*arr)[COL2]) {
	for(int i=0;i<ROW1;i++) {
		for(int j=0;j<COL2;j++)
			cout<<arr[i][j]<<" ";
		cout<<endl;
	}
}

int main()
{
    double arr1[ROW1][COL1] = {1,2,3,1,2,3,1,2,3};
    double arr2[ROW2][COL2] = {1,1,1,1,1,1,1,1,1};
    double arr3[ROW1][COL2] = {0};
    matrix_mutiplicate(arr1,arr2,arr3);
    matrix_print(arr3);
	return 0;   	  		   		 
}

输出结果：

c++矩阵相乘,# 数学与编程,矩阵,c++,线性代数