区间预测 | MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测
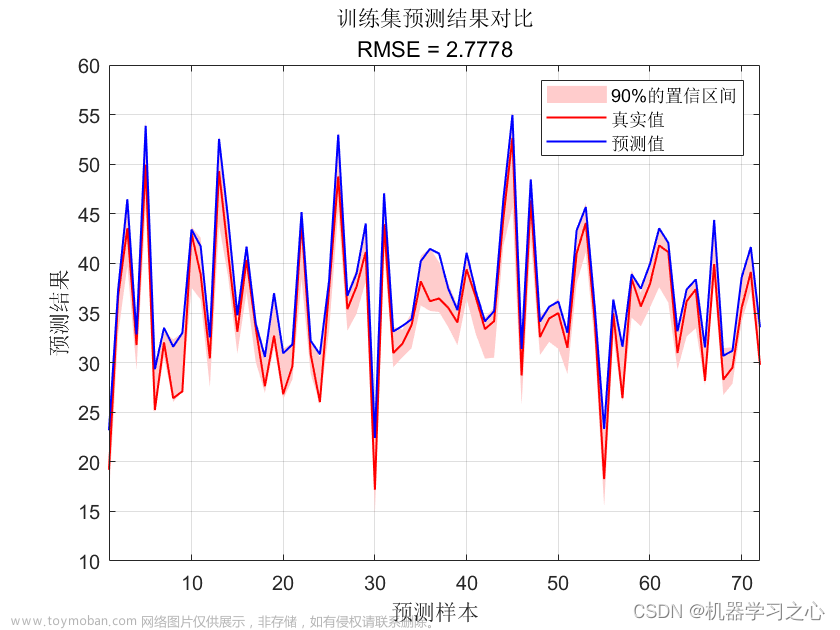
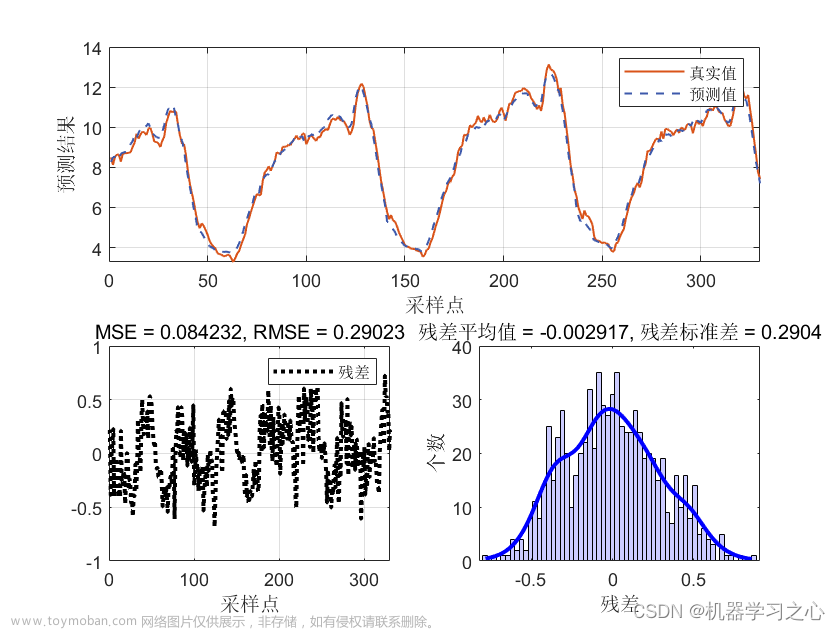
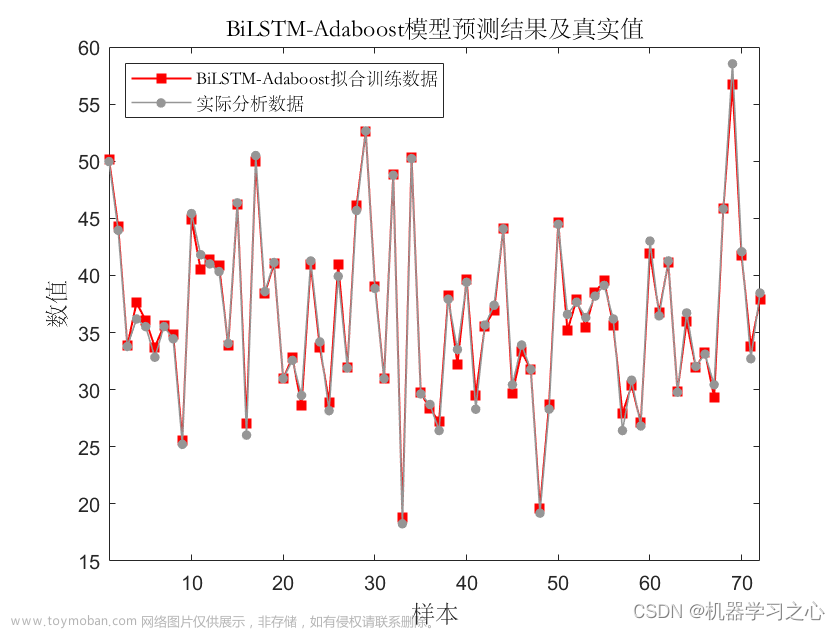
效果一览




基本介绍
区间预测 | MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测
QRBiLSTM是一种双向长短期记忆(QR-LSTM)神经网络的变体,用于分位数回归时间序列区间预测。该模型可以预测时间序列的不同分位数的值,并且可以提供置信区间和风险评估等信息。
QR-LSTM是一种基于LSTM模型的分位数回归方法,可以通过学习分位数回归损失函数来预测不同分位数的值。而QRBiLSTM则是在QR-LSTM的基础上加入了双向传输的结构,可以捕捉更多的时间序列信息。
模型描述
QRBiLSTM模型的输入包括历史数据,输出为分位数值和置信区间。通常情况下,可以使用训练数据来拟合模型参数,并使用测试数据来评估模型的预测性能。
总之,QRBiLSTM是一种非常有用的时间序列预测模型,可以应用于许多领域,如金融、股票、气象学等,可以提供更全面的时间序列预测信息,有助于提高决策的准确性。
-
下面给出QRBiLSTM模型的具体公式,其中 X \textbf{X} X表示输入序列, Y \textbf{Y} Y表示输出序列, H \textbf{H} H表示隐藏状态, C \textbf{C} C表示记忆状态, f θ f_{\theta} fθ表示神经网络模型, q q q表示分位数:
-
正向传播:
H t f , C t f = L S T M θ ( X t , H t − 1 f , C t − 1 f ) \textbf{H}^{f}_{t},\textbf{C}^{f}_{t} = LSTM_{\theta}(\textbf{X}_{t},\textbf{H}^{f}_{t-1},\textbf{C}^{f}_{t-1}) Htf,Ctf=LSTMθ(Xt,Ht−1f,Ct−1f)
H t b , C t b = L S T M θ ( X t , H t + 1 b , C t + 1 b ) \textbf{H}^{b}_{t},\textbf{C}^{b}_{t} = LSTM_{\theta}(\textbf{X}_{t},\textbf{H}^{b}_{t+1},\textbf{C}^{b}_{t+1}) Htb,Ctb=LSTMθ(Xt,Ht+1b,Ct+1b)
Y ^ t q = f θ ( [ H t f , H t b ] ) \hat{Y}^{q}_{t} = f_{\theta}([\textbf{H}^{f}_{t},\textbf{H}^{b}_{t}]) Y^tq=fθ([Htf,Htb])
ϵ ^ t q = Y t q − Y ^ t q \hat{\epsilon}^{q}_{t} = Y^{q}_{t} - \hat{Y}^{q}_{t} ϵ^tq=Ytq−Y^tq
σ ^ t q = median { ∣ ϵ ^ t − τ q ∣ : τ ≤ lag } ⋅ c α ( lag , n ) \hat{\sigma}^{q}_{t} = \text{median}\{|\hat{\epsilon}^{q}_{t-\tau}|:\tau \leq \text{lag}\} \cdot c_{\alpha}(\text{lag},n) σ^tq=median{∣ϵ^t−τq∣:τ≤lag}⋅cα(lag,n)
-
其中, H t f \textbf{H}^{f}_{t} Htf和 C t f \textbf{C}^{f}_{t} Ctf分别表示正向传播的隐藏状态和记忆状态; H t b \textbf{H}^{b}_{t} Htb和 C t b \textbf{C}^{b}_{t} Ctb分别表示反向传播的隐藏状态和记忆状态; Y ^ t q \hat{Y}^{q}_{t} Y^tq表示时间 t t t处分位数为 q q q的预测值; f θ f_{\theta} fθ表示神经网络模型; ϵ ^ t q \hat{\epsilon}^{q}_{t} ϵ^tq表示时间 t t t处分位数为 q q q的预测误差; σ ^ t q \hat{\sigma}^{q}_{t} σ^tq表示时间 t t t处分位数为 q q q的预测误差的置信区间,其中 c α ( lag , n ) c_{\alpha}(\text{lag},n) cα(lag,n)表示置信系数。
-
QRBiLSTM模型的训练目标是最小化分位数损失函数:
Loss θ = ∑ t = 1 T ∑ q ∈ Q ρ q ( ∣ ϵ t q ∣ ) − 1 ∣ Q ∣ ∑ q ∈ Q log ( σ ^ t q ) \text{Loss}_{\theta}=\sum_{t=1}^{T}\sum_{q\in Q}\rho_{q}(|\epsilon^{q}_{t}|)-\frac{1}{|Q|}\sum_{q\in Q}\text{log}(\hat{\sigma}^{q}_{t}) Lossθ=t=1∑Tq∈Q∑ρq(∣ϵtq∣)−∣Q∣1q∈Q∑log(σ^tq)
- 其中, ρ q ( x ) \rho_{q}(x) ρq(x)表示分位数损失函数:
ρ q ( x ) = { q x x ≥ 0 ( q − 1 ) x x < 0 \rho_{q}(x)=\begin{cases}qx&x\geq 0\\(q-1)x&x<0\end{cases} ρq(x)={qx(q−1)xx≥0x<0文章来源:https://www.toymoban.com/news/detail-653644.html
- QRBiLSTM模型的预测目标是预测分位数值和置信区间,即 Y ^ t q \hat{Y}^{q}_{t} Y^tq和 σ ^ t q \hat{\sigma}^{q}_{t} σ^tq。
程序设计
- 完整程序和数据获取方式(资源处下载):MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测
% 构建模型
numFeatures = size(XTrain,1); % 输入特征数
numHiddenUnits = 200; % 隐藏单元数
numQuantiles = 1; % 分位数数目
layers = [ ...
sequenceInputLayer(numFeatures)
bilstmLayer(numHiddenUnits,'OutputMode','last')
dropoutLayer(0.2)
fullyConnectedLayer(numQuantiles)
regressionLayer];
options = trainingOptions('adam', ...
'MaxEpochs',50, ...
'MiniBatchSize',64, ...
'GradientThreshold',1, ...
'Shuffle','every-epoch', ...
'Verbose',false);
net = trainNetwork(XTrain,YTrain,layers,options); % 训练模型
% 测试模型
YPred = predict(net,XTest); % 预测输出
quantiles = [0.1,0.5,0.9]; % 分位数
for i = 1:length(quantiles)
q = quantiles(i);
epsilon = YTest - YPred(:,i); % 预测误差
lag = 10; % 滞后期数
sigma = median(abs(epsilon(max(1,end-lag+1):end))) * 1.483; % 置信区间
lb = YPred(:,i) - sigma * norminv(1-q/2,0,1); % 置信区间下限
ub = YPred(:,i) + sigma * norminv(1-q/2,0,1); % 置信区间上限
disp(['Quantile:',num2str(q),' MAE:',num2str(mean(abs(epsilon))),' Width:',num2str(mean(ub-lb))]);
end
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340文章来源地址https://www.toymoban.com/news/detail-653644.html
到了这里,关于区间预测 | MATLAB实现QRBiLSTM双向长短期记忆神经网络分位数回归时间序列区间预测的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!