从前序与中序遍历序列构造二叉树，从中序与后序遍历序列构造二叉树-Toy模板网

这篇具有很好参考价值的文章主要介绍了从前序与中序遍历序列构造二叉树，从中序与后序遍历序列构造二叉树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

从前序与中序遍历序列构造二叉树

题目链接

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

实例1:
从前序与中序遍历序列构造二叉树，从中序与后序遍历序列构造二叉树,leetcode,算法,数据结构,c++

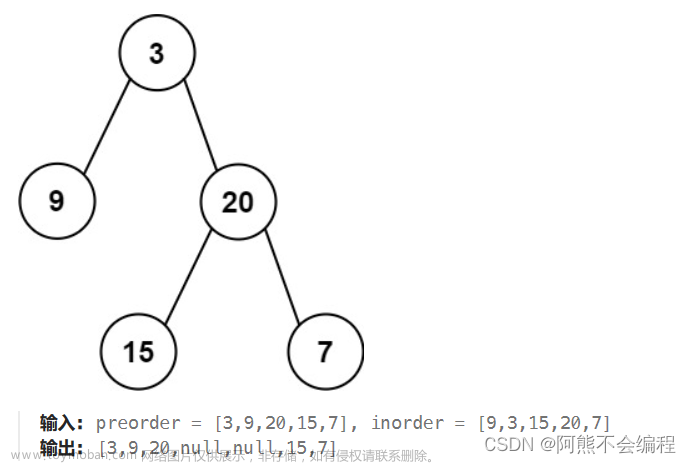
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

首先我们应该明白，
前序遍历就是，先遍历根节点，然后遍历左子树，最后遍历右子树
中序遍历就是，先遍历左子树，然后遍历根节点，最后遍历右子树
后续遍历就是，先遍历左子树，然后遍历右子树，最后遍历根节点

首先我们先试着用前序与中序遍历序列构造一棵二叉树

给出前序遍历数列 preorder 和中序遍历数列 inorder
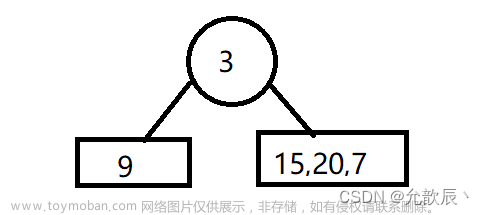
我们知道前序遍历二叉树必然先走根节点，所以我们可知preorder序列中的第一个数字3即为二叉树的根节点，中序遍历数列中，左子树必然先于右子树遍历，所以我们可知，在中序遍历数列inorder中的使用根节点将inorder划分为三个区间，（左子树）根（右子树），根节点3左边的元素为左子树，3右边的元素为右子树

现在3的左子树为空，右子树（15，20，7）继续使用相同方法构造二叉树

代码：文章来源地址https://www.toymoban.com/news/detail-656415.html

采用递归调用，分解子问题的方法

class Solution {
public:
    TreeNode* build(vector<int>& preorder,vector<int>& inorder,
                        int& prev,int inbegin,int inend)
    {	//perorder 前序遍历序列，inorder 中序遍历序列,prev 指向前序遍历数列下标
        if(inbegin>inend)return NULL;
        //当前的根节点
        TreeNode* root=new TreeNode(preorder[prev]);
        int rooti=inbegin; //用来查找根节点在数组中的下班位置
        while(rooti<inend)
        {
            if(inorder[rooti]==preorder[prev])break;
            rooti++;
        }
        prev++;  //每次使用完prev需往后走，prev指的是数组前序遍历中用来判断根节点的
        //划分区间，（左子树，根）根（根，右子树）
        // （inbegin,rooti-1）rooti（rooti+1,inend）
        //函数递归继续构造二叉树的左右节点
        root->left=build(preorder,inorder,prev,inbegin,rooti-1); 
        root->right=build(preorder,inorder,prev,rooti+1,inend);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int i=0;
        TreeNode* root=build(preorder,inorder,i,0,inorder.size()-1);
        return root;
    }
};

从中序与后序遍历序列构造二叉树

题目链接

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

实例1：

从前序与中序遍历序列构造二叉树，从中序与后序遍历序列构造二叉树,leetcode,算法,数据结构,c++

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

使用中序与后序遍历序列构造二叉树思路根前序与中序序列构造二叉树相似

给出二叉树的中序遍历inorder 和后续遍历 postorder

我们知道后续遍历二叉树，根节点最后遍历，所以我们可知postorder序列中的最后一个元素3即为二叉树的根节点，中序遍历数列中，左子树优于根先遍历，右子树后于根遍历，所以我们可以根据这两个条件将inorder序列划分为三个区间，（左子树）根（右子树）,根节点3左边的元素为左子树，3右边的元素为右子树

3的左子树序列只剩一个，即为3的左节点，右子树序列还有三个元素，需要继续划分，重复上述过程

代码：

class Solution {
public:
    TreeNode* build(vector<int>& inorder, vector<int>& postorder,
                    int& prev,int inbegin,int inend)
    {
        if(inbegin>inend)return NULL;
        TreeNode* root=new TreeNode(postorder[prev]);
        int rooti=inbegin;
        while(rooti<inend)
        {
            if(postorder[prev]==inorder[rooti])break;
            rooti++;
        }
        prev--;
        //  （左，根）根（根，右）
        //先构造右子树，再构造左子树
        root->right=build(inorder,postorder,prev,rooti+1,inend);
        root->left=build(inorder,postorder,prev,inbegin,rooti-1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int i=postorder.size()-1;
        TreeNode* root=build(inorder,postorder,i,0,postorder.size()-1);
        return root;
    }
};