函数递归（详解）-Toy模板网

这篇具有很好参考价值的文章主要介绍了函数递归（详解）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一.什么是函数递归？

首先我们可以从字面上来解释一下：
递归的递：可以理解为递推
递归的归：可以理解为回归

接下来我们来看看递归的定义：

程序调用自身的编程技巧称为递归（ recursion）。
递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法。
它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。

函数递归的思考方式：把大事化小

1.函数递归的优点

只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

2.函数递归缺点

如果递归层次太深容易造成死递归，最后导致程序崩掉。
有时侯递归的效率会很低。

二.函数递归的两个限制条件

1.存在限制条件，当满足这个限制条件的时候，递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件

三.递归试题

在简单了解递归是什么之后，接下来我将会用几个列子带大家更加深刻的了解递归。

试题1

接受一个整型值(无符号)，按照顺序打印它的每一位
列如输入1234 ，打印 1 2 3 4

先上思路：
递归函数,小路_C语言学习,算法,c语言,c++

接下来让我们用代码来实现它

void Print(int n)
{
	if (n > 9) //限制条件
	{
		Print(n / 10);//无限的接近限制条件
	}
	printf("%d ", n % 10);
}
int main()
{
	int n = 0;
	scanf("%d", &n);

	Print(n);

	return 0;
}

运行结果：
递归函数,小路_C语言学习,算法,c语言,c++

如果在这里大家还不是很清晰的明白的话，不要慌，我们来画图解释一下

递归函数,小路_C语言学习,算法,c语言,c++

这样大家是不是可以更好的理解了。

试题2

编写函数（不允许创建临时变量），求字符串的长度。
在这里的话不创建临时变量，其实就是要求你用递归方法

直接上代码：

int my_strlen(char* arr)
{
	if (*arr != '\0')
	{
		return 1 + my_strlen(arr + 1);
	}
	else //第一个就是\0
	{
		return 0;
	}
}
int main()
{
	char arr[] = "hello";

	int len = my_strlen(arr);
	
	printf("%d ", len);
	return 0;
}

运行结果：
递归函数,小路_C语言学习,算法,c语言,c++

试题3

求n的阶乘。（不考虑溢出）

递归写法

int fac(int n)
{
	if (n > 1)
	{
		return n * jiech(n - 1);
	}
	else
	{
		return 1;
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);

	int sum = fac(n);
	printf("%d\n", sum);
	return 0;
}

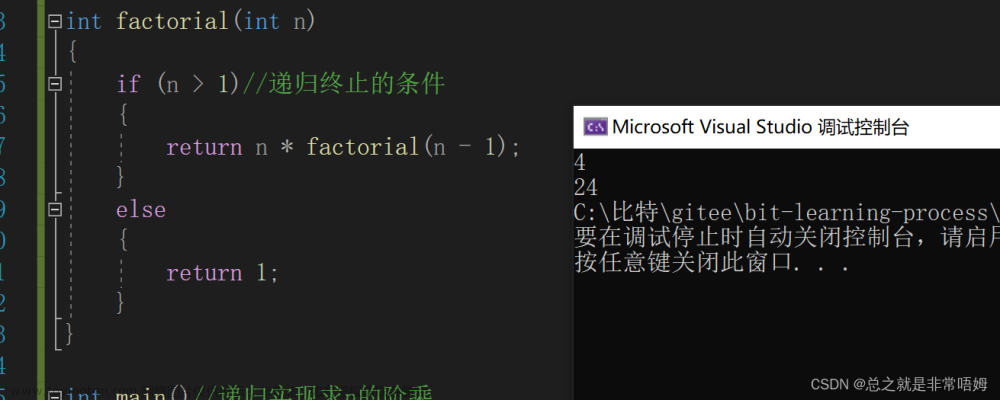
接下来我们来看一下运行结果
递归函数,小路_C语言学习,算法,c语言,c++

非递归写法

int fac(int n)
{
	int i = 0;
	int sum = 1;
	for (i = 1; i <= n; i++)
	{
		sum *= i;
	}
	return sum;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = fac(n);
	printf("%d\n", ret);
	return 0;
}

试题四

求第n个斐波那契额数列

递归写法

int Fe(int n)
{
	if (n <= 2)
	{
		return 1;
	}
	else
	{
		return Fe(n - 1) + Fe(n - 2);
	}
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fe(n);
	printf("%d\n", ret);
	return 0;
}

两种运行结果
输入10
递归函数,小路_C语言学习,算法,c语言,c++

输入50
递归函数,小路_C语言学习,算法,c语言,c++
此时我们发现光标一直闪烁，说明此时计算机在努力的计算

非递归写法

int Fe(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	while (n >= 3)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	return c;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fe(n);
	printf("%d\n", ret);
	return 0;
}