机器学习笔记之优化算法(十五)Baillon Haddad Theorem简单认识

引言

本节将简单认识$\text{Baillon Haddad Theorem}$(白老爹定理)，并提供相关证明。

Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem简单认识

如果函数$f(\cdot )$在其定义域内可微，并且是凸函数，则存在如下等价条件：
以下几个条件之间相互等价。

• 关于$f(\cdot )$的梯度$\nabla f(\cdot )$满足$\mathcal{L}$-利普希兹连续；
  $$\{\begin{array}{l}\forall x,\hat{x}\in {\mathbb{R}}^n,\exists \mathcal{L}:s.t.||f(x)-f(\hat{x})||\le \mathcal{L}\cdot ||x-\hat{x}||\\ \\ \begin{array}{r}\exists \xi \in (x,\hat{x})\Rightarrow \frac{||f(x)-f(\hat{x})||}{||x-\hat{x}||}=f^{\prime }(\xi )\le \mathcal{L}\end{array}\end{array}$$
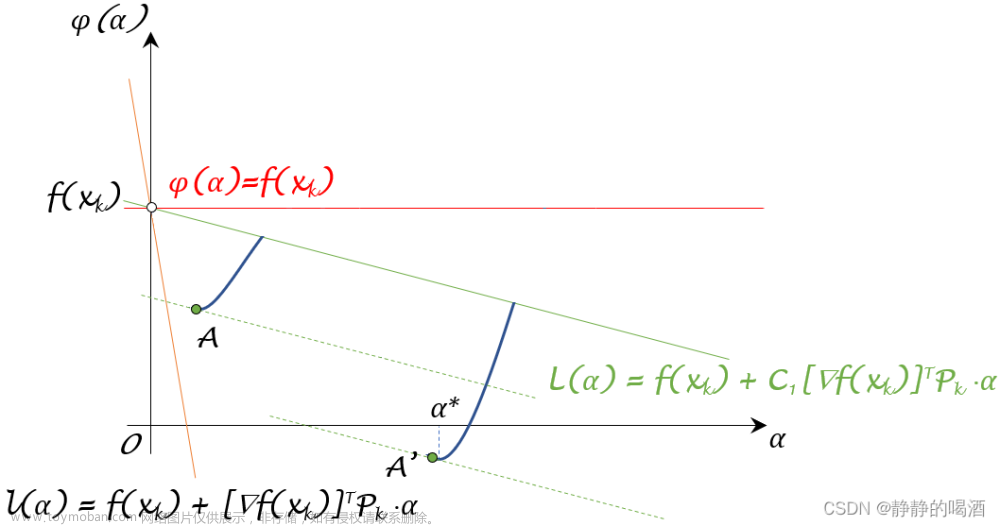
  关于利普希兹连续详见二次上界引理。从逻辑的角度理解，这意味着：函数$f(\cdot )$中斜率的变化量被利普希兹常数$\mathcal{L}$约束。从图像的角度模糊观察，由于$\mathcal{L}$的限制，不会出现斜率过于陡峭的情况。
  见下图。从$x\Rightarrow y$的过程中，$\nabla f(x)\Rightarrow \nabla f(y)$发生了剧烈的变化。这本质上说明$f(\cdot )$在$[x,y]$区间内过于陡峭的原因。
  

• 关于函数$\begin{array}{r}\mathcal{G}(x)=\frac{\mathcal{L}}{2}{x}^{T}x-f(x)\end{array}$同样是凸函数。

  观察$\mathcal{G}(x)$，可以发现它由两部分组成：系数是$\begin{array}{r}\frac{\mathcal{L}}{2}\end{array}$，关于变量$x$的二次项结果；以及$f(x)$自身。而二次函数$\begin{array}{r}\frac{\mathcal{L}}{2}{x}^{T}x\end{array}$其自身一定是个凸函数。该条件意味着：这两个凸函数的差也是凸函数。

  如果从逻辑角度对$\begin{array}{r}\frac{\mathcal{L}}{2}{x}^{T}x-f(x)\end{array}$进行认知：两个凸函数之间做减法，若$f(x)$的陡峭程度要高于$\begin{array}{r}\frac{\mathcal{L}}{2}{x}^{T}x\end{array}$，这势必使得减法结果可能不是凸函数；因而该等价条件的本质依然是：约束$f(x)$斜率的变化率，而该变化率的约束与利普希兹常数$\mathcal{L}$存在关联关系。

• 关于函数的梯度$\nabla f(\cdot )$具有余强制性$(\text{Co-coercive})$。即：
  $${\left[\nabla f(x)-\nabla f(y)\right]}^T(x-y)\ge \frac{1}{\mathcal{L}}||\nabla f(x)-\nabla f(y)|{|}^2$$
  首先解释一下强制性$(\text{Coercive})$。它也被称作强单调性$(\text{Strongly monotonicity})$。从名字可以看出来——它比一般的单调性更强。关于$f(\cdot ):\mathbb{R}\mapsto \mathbb{R}$，其单调性的定义表示为：

  • 自变量的差异性与对应函数差异性之间同号。
  • 关于$n$维的特征空间$f(\cdot ):{\mathbb{R}}^n\mapsto {\mathbb{R}}^n$,那么此时的$f(x)-f(y)$与$x-y$都是向量。对应单调性的定义即：$[f(x)-f(y){]}^T(x-y)\ge 0$
    $$\forall x,y\in \mathbb{R}s.t.[f(x)-f(y)]\cdot (x-y)\ge 0$$

  而强单调性在单调性同号的基础上，进行了更强的约束：将式子右侧的$0$替换为一个恒正的值。该值通常表示为：系数$\alpha$与$x$的增量$||x-y|{|}^2$的乘积形式：
  $$[f(x)-f(y){]}^T(x-y)\ge \alpha \cdot ||x-y|{|}^2$$
  若该值使用$f(x)$的增量进行表示，我们称之为余强制性，也被称作逆向强单调性$(\text{Inverse Strongly monotonicity})$：
  $$[f(x)-f(y){]}^T(x-y)\ge \alpha \cdot ||f(x)-f(y)|{|}^2$$
  回顾等价条件$3$：不等式左侧就是$\nabla f(\cdot )$单调性的定义；不等式右侧则是关于余强制性的表述。需要关注的点在于：参与描述正值的系数$\alpha$与利普希兹常数$\mathcal{L}$之间存在关联关系：$\begin{array}{r}\alpha =\frac{1}{\mathcal{L}}\end{array}$。

证明过程

通过证明：条件$1\Rightarrow$条件$2$，条件$2\Rightarrow$条件$3$,条件$3\Rightarrow$条件$1$来实现$3$个条件之间的等价关系。

证明：条件$1\Rightarrow$ 条件$2$

若$f(\cdot )$是凸函数，在定义域内可微；并且梯度函数$\nabla f(\cdot )$满足$\mathcal{L}$-利普希兹连续，求证：函数$\begin{array}{r}\mathcal{G}(x)=\frac{\mathcal{L}}{2}{x}^{T}x-f(x)\end{array}$是凸函数。
关于凸函数的一种证法在于，证明该函数的梯度满足单调性。之所以引入梯度的另一个原因是可以将$\begin{array}{r}\frac{\mathcal{L}}{2}{x}^{T}x\end{array}$化成一次项。

证明过程：由$\begin{array}{r}\mathcal{G}(x)=\frac{\mathcal{L}}{2}{x}^{T}x-f(x)\end{array}$可知，关于$\mathcal{G}(x)$梯度$\nabla \mathcal{G}(x)$可表示为：
$$\nabla \mathcal{G}(x)=\mathcal{L}\cdot x-\nabla f(x)$$
至此，观察$\nabla \mathcal{G}(x)$的单调性：
仅需证明$\mathcal{I}\ge 0$恒成立即可。
$$\forall x_1,x_2\in {\mathbb{R}}^n\Rightarrow \mathcal{I}=[\nabla \mathcal{G}(x_1)-\nabla \mathcal{G}(x_2){]}^T(x_1-x_2)$$
将上述梯度结果代入，有：
继续展开~
$$\begin{array}{rl}\mathcal{I}& =[\mathcal{L}\cdot x_1-\nabla f(x_1)-\mathcal{L}\cdot x_2+\nabla f(x_2){]}^T(x_1-x_2)\\ & =\mathcal{L}\cdot (x_1-x_2{)}^T(x_1-x_2)-[\nabla f(x_1)-\nabla f(x_2){]}^T(x_1-x_2)\end{array}$$
观察后一项：$-[\nabla f(x_1)-\nabla f(x_2){]}^T(x_1-x_2)$，这明显是两个向量的内积形式。可以根据柯西施瓦茨不等式，得到如下结果：
该部分同样可以使用向量乘法描述:$a^{T}b=|a|\cdot |b|\cdot \cos \theta \le |a|\cdot |b|$因为$\cos \theta \in [-1,1]\le 1$。
$$[\nabla f(x_1)-\nabla f(x_2){]}^T(x_1-x_2)\le ||\nabla f(x_1)-\nabla f(x_2)||\cdot ||x_1-x_2||$$
加上负号与前一项，从而有：
至于$(x_1-x_2{)}^T(x_1-x_2)=||x_1-x_2|{|}^2$,两向量重合，夹角为$0$。
$$\mathcal{I}\ge \mathcal{L}\cdot ||x_1-x_2|{|}^2-||\nabla f(x_1)-\nabla f(x_2)||\cdot ||x_1-x_2||$$
由于梯度函数$\nabla f(\cdot )$满足$\mathcal{L}$-利普希兹连续，因而将$||\nabla f(x_1)-\nabla f(x_2)||\le \mathcal{L}\cdot ||x_1-x_2||$，对上式中的$||\nabla f(x_1)-\nabla f(x_2)||$进行替换，最终不等号的方向不发生变化：
$$\{\begin{array}{l}-||\nabla f(x_1)-\nabla f(x_2)||\ge -\mathcal{L}\cdot ||x_1-x_2||\\ \\ \begin{array}{rl}\mathcal{I}& \ge \mathcal{L}\cdot ||x_1-x_2|{|}^2-||\nabla f(x_1)-\nabla f(x_2)||\cdot ||x_1-x_2||\\ & \ge \mathcal{L}\cdot ||x_1-x_2|{|}^2-(\mathcal{L}\cdot ||x_1-x_2||)\cdot |||x_1-x_2||\\ & =0\end{array}\end{array}$$

最终可证明：$\mathcal{I}\ge 0\Rightarrow$梯度函数$\nabla \mathcal{G}(x)$有单调性。从而函数$\mathcal{G}(x)$是凸函数。

证明：条件$3\Rightarrow$条件$1$

若梯度函数$\nabla f(\cdot )$有余强制性，那么该梯度函数$\nabla f(\cdot )$满足$\mathcal{L}$-利普希兹连续。

证明过程：基于$\nabla f(\cdot )$余强制性，结合柯西施瓦茨不等式，有：
使用柯西施瓦茨不等式将不等式左侧表示为模的乘积形式。
$$\{\begin{array}{l}\begin{array}{rl}{\left[\nabla f(x)-\nabla f(y)\right]}^T(x-y)& \ge \frac{1}{\mathcal{L}}||\nabla f(x)-\nabla f(y)|{|}^2\\ & \Downarrow \\ ||\nabla f(x_1)-\nabla f(x_2)||\cdot ||x_1-x_2||& \ge [\nabla f(x_1)-\nabla f(x_2){]}^T(x_1-x_2)\\ & \ge \frac{1}{\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2\end{array}\end{array}$$
消去$||\nabla f(x_1)-\nabla f(x_2)||$，整理有：
$$||\nabla f(x_1)-\nabla f(x_2)||\le \mathcal{L}\cdot ||x_1-x_2||$$
从而得证：$\nabla f(\cdot )$满足$\mathcal{L}$-利普希兹连续。

证明：条件$2\Rightarrow$条件$3$

若$\begin{array}{r}\mathcal{G}(x)=\frac{\mathcal{L}}{2}{x}^{T}x-f(x)\end{array}$是凸函数，那么关于梯度函数$\nabla f(\cdot )$有余强制性。

证明思路：在证明之前，引入几个辅助变量：
将余强制性不等式左侧$[\nabla f(x_1)-\nabla f(x_2){]}^T(x_1-x_2)$记作$\Delta$，并将其分解为如下形式：

• 其中将$x_1-x_2$转化成$-(x_2-x_1)$,并将负号提出来。
• 其中$[\nabla f(x_1)-\nabla f(x_2){]}^T=\left\{[\nabla f(x_1){]}^T-[\nabla f(x_2){]}^T\right\}$。
  Δ = [ f ( x 1 ) + f ( x 2 ) ] − [ f ( x 1 ) + f ( x 2 ) ] ⏟ = 0 − { [ ∇ f ( x 1 ) ] T − [ ∇ f ( x 2 ) ] T } ( x 2 − x 1 ) = f ( x 2 ) − { f ( x 1 ) + [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) } ⏟ Δ 1 + f ( x 1 ) − { f ( x 2 ) + [ ∇ f ( x 2 ) ] T ( x 1 − x 2 ) } ⏟ Δ 2 = Δ 1 + Δ 2 \begin{aligned} \Delta & = \underbrace{[f(x_1) + f(x_2)] - [f(x_1) + f(x_2)]}_{=0} - \left\{[\nabla f(x_1)]^T - [\nabla f(x_2)]^T\right\}(x_2 - x_1) \\ & = \underbrace{f(x_2) - \{f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1)\}}_{\Delta_1} + \underbrace{f(x_1) - \left\{f(x_2) + [\nabla f(x_2)]^T(x_1 - x_2)\right\}}_{\Delta_2} \\ & = \Delta_1 + \Delta_2 \end{aligned} Δ​==0 [f(x1​)+f(x2​)]−[f(x1​)+f(x2​)]​​−{[∇f(x1​)]T−[∇f(x2​)]T}(x2​−x1​)=Δ1​ f(x2​)−{f(x1​)+[∇f(x1​)]T(x2​−x1​)}​​+Δ2​ f(x1​)−{f(x2​)+[∇f(x2​)]T(x1​−x2​)}​​=Δ1​+Δ2​​

可以在图像中描述出${\Delta }_1,{\Delta }_2$的表示：

• 其中$f(x_1)+[\nabla f(x_1){]}^T(x_2-x_1)$表示过点$x_1$的$f(\cdot )$的切线，与$x=x_2$相交后，到点$x_2$的距离。见黄色实线部分；
• 对应${\Delta }_1$则表示：$f(x_2)$与$f(x_1)+[\nabla f(x_1){]}^T(x_2-x_1)$之间的距离差值。见红色实线部分。
• 同理，关于${\Delta }_2$的图像描述表示为：
  对应的${\Delta }_2$表示为图中的绿色实线部分。
  
  如果${\Delta }_1$或者${\Delta }_2$满足：$\begin{array}{r}{\Delta }_1;{\Delta }_2\ge \frac{1}{2\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2\end{array}$即可。

证明过程：
这里以${\Delta }_1$为例，将${\Delta }_1$展开，有：
$$\begin{array}{rl}{\Delta }_1& =\underset{1}{f(x_2)-[\nabla f(x_1){]}^T{x}_2}-\underset{2}{\left\{f(x_1)-[\nabla f(x_1){]}^T{x}_1\right\}}\end{array}$$
可以发现，上述的$1,2$两个部分存在相同的格式。因此假设一个函数：
关于函数${\mathcal{H}}_{x_1}(\mathcal{Z})$,其中$\mathcal{Z}$是自变量，而内部的$x_1$被视作可变参数。
$${\mathcal{H}}_{x_1}(\mathcal{Z})=f(\mathcal{Z})-[\nabla f(x_1){]}^T\mathcal{Z}$$
从而${\Delta }_1$可表示为：
$${\Delta }_1={\mathcal{H}}_{x_1}(x_2)-{\mathcal{H}}_{x_1}(x_1)$$
观察${\mathcal{H}}_{x_1}(\mathcal{Z})$函数，其中$f(\mathcal{Z})$是关于$\mathcal{Z}$的凸函数；而$-[\nabla f(x_1){]}^T\mathcal{Z}$本质上是关于$\mathcal{Z}$的一次函数，自然也是凸函数。根据保凸运算可知，${\mathcal{H}}_{x_1}(\mathcal{Z})$一定是一个凸函数；并且由于$f(\mathcal{Z})$与$-[\nabla f(x_1){]}^T\mathcal{Z}$均在$\mathcal{Z}$定义域内可微，因而${\mathcal{H}}_{x_1}(\mathcal{Z})$同样可微。因而${\mathcal{H}}_{x_1}(\mathcal{Z})$关于$\mathcal{Z}$的梯度$\nabla {\mathcal{H}}_{x_1}(\mathcal{Z})$可表示为：
$$\begin{array}{r}\nabla {\mathcal{H}}_{x_1}(\mathcal{Z})=\nabla f(\mathcal{Z})-\nabla f(x_1)\end{array}$$
当$\mathcal{Z}=x_1$时，有：$\nabla {\mathcal{H}}_{x_1}(x_1)=0$。这意味着：$\mathcal{Z}=x_1$是函数${\mathcal{H}}_{x_1}(\mathcal{Z})$的极值点。而又因为${\mathcal{H}}_{x_1}(\mathcal{Z})$的凸函数性质，因而该点一定是最小值点。记${\mathcal{H}}_{x_1}(\mathcal{Z})$的最小值结果为${\mathcal{H}}_{x_1}^{\ast }$，从而可得：
$${\mathcal{H}}_{x_1}^{\ast }={\mathcal{H}}_{x_1}(x_1)$$
根据条件$2$：$\begin{array}{r}\mathcal{G}(\mathcal{Z})=\frac{\mathcal{L}}{2}{\mathcal{Z}}^T\mathcal{Z}-f(\mathcal{Z})\end{array}$是凸函数，将$f(\mathcal{Z})={\mathcal{H}}_{x_1}(\mathcal{Z})+[\nabla f(x_1){]}^T\mathcal{Z}$代入到条件$2$中有：
这里将变量符号$x$替换成变量符号$\mathcal{Z}$,便于下面的计算，并将${\mathcal{Z}}^T\mathcal{Z}$使用$||\mathcal{Z}|{|}^2$替代。
$$\begin{array}{rl}\mathcal{G}(\mathcal{Z})& =\frac{\mathcal{L}}{2}||\mathcal{Z}|{|}^2-f(\mathcal{Z})\\ & =\frac{\mathcal{L}}{2}||\mathcal{Z}|{|}^2-{\mathcal{H}}_{x_1}(\mathcal{Z})-[\nabla f(x_1){]}^T\mathcal{Z}\\ & \\ \Rightarrow \mathcal{G}(\mathcal{Z})+& [\nabla f(x_1){]}^T\mathcal{Z}=\frac{\mathcal{L}}{2}||\mathcal{Z}|{|}^2-{\mathcal{H}}_{x_1}(\mathcal{Z})\end{array}$$
观察上式的等号左侧：$\mathcal{G}(\mathcal{Z})+[\nabla f(x_1){]}^T\mathcal{Z}$，同样可以如法炮制${\mathcal{H}}_{x_1}(\mathcal{Z})=f(\mathcal{Z})+[\nabla f(x_1){]}^T\mathcal{Z}$一样，定义一个符号${\mathcal{G}}_{x_1}(\mathcal{Z})$，使得：
$${\mathcal{G}}_{x_1}(\mathcal{Z})=\mathcal{G}(\mathcal{Z})+[\nabla f(x_1){]}^T\mathcal{Z}$$
观察${\mathcal{G}}_{x_1}(\mathcal{Z})$的相关性质：

• 关于第一项，根据条件$2$描述：$\mathcal{G}(\mathcal{Z})$自身是凸函数，可微；
• 关于第二项与${\mathcal{H}}_{x_1}(\mathcal{Z})$的第二项相同：关于$\mathcal{Z}$的一次函数$[\nabla f(x_1){]}^T\mathcal{Z}$同样是凸函数，并在自身定义域内可微。

综上，依然可以根据保凸运算，关于函数${\mathcal{G}}_{x_1}(\mathcal{Z})$也是凸函数，并在定义域内可微。从而该函数的梯度$\nabla {\mathcal{G}}_{x_1}(\mathcal{Z})$表示如下：
$$\begin{array}{rl}\nabla {\mathcal{G}}_{x_1}(\mathcal{Z})& =\frac{\mathcal{L}}{2}\cdot 2\cdot \mathcal{Z}-\nabla {\mathcal{H}}_{x_1}(\mathcal{Z})\\ & =\mathcal{L}\cdot \mathcal{Z}-\nabla {\mathcal{H}}_{x_1}(\mathcal{Z})\end{array}$$
根据${\mathcal{G}}_{x_1}(\mathcal{Z})$凸函数的性质，在$\mathcal{Z}$定义域内取$z_1\le z_2,z_1,z_2\in \mathbb{R}$，必然有：
$${\mathcal{G}}_{x_1}(z_2)\ge {\mathcal{G}}_{x_1}(z_1)+{\left[\nabla {\mathcal{G}}_{x_1}(z_1)\right]}^T(z_2-z_1)$$
从上述图像中观察更加直观。也就是说：${\Delta }_1\ge 0$恒成立。将上述$\begin{array}{r}{\mathcal{G}}_{x_1}(\mathcal{Z})=\frac{\mathcal{L}}{2}||\mathcal{Z}|{|}^2-{\mathcal{H}}_{x_1}(\mathcal{Z})\end{array}$代入，有：
$$\underset{{\mathcal{G}}_{x_1}(z_2)}{\frac{\mathcal{L}}{2}||z_2|{|}^2-{\mathcal{H}}_{x_1}(z_2)}\ge \underset{{\mathcal{G}}_{x_1}(x_1)}{\frac{\mathcal{L}}{2}||z_1|{|}^2-{\mathcal{H}}_{x_1}(z_1)}+\underset{[{\mathcal{G}}_{x_1}(z_1){]}^T}{[\mathcal{L}\cdot z_1-\nabla {\mathcal{H}}_{x_1}(z_1){]}^T}\cdot (z_2-z_1)$$
至此，描述${\mathcal{G}}_{x_1}(\mathcal{Z})$凸函数性质的式子全部由${\mathcal{H}}_{x_1}(\mathcal{Z})$进行代替。经过整理，有：
对比一下二次上界引理,它们确实比较相似，但并不是。因为$\begin{array}{r}\frac{\mathcal{L}}{2}||z_2|{|}^2-\frac{\mathcal{L}}{2}||z_1|{|}^2\end{array}$与$\begin{array}{r}\frac{\mathcal{L}}{2}||z_2-z_1|{|}^2\end{array}$绝大多数情况不相等。
$${\mathcal{H}}_{x_1}(z_2)\le \frac{\mathcal{L}}{2}||z_2|{|}^2-\frac{\mathcal{L}}{2}||z_1|{|}^2+{\mathcal{H}}_{x_1}(z_1)+{\left[\nabla {\mathcal{H}}_{x_1}(z_1)-\mathcal{L}\cdot z_1\right]}^T(z_2-z_1)$$
但该式子并不影响我们使用二次上界引理中的操作：将$z_1$视作上一次迭代产生的数值解，因而$z_1$是已知项，从而不等式右侧是关于$z_2$的函数，记作$\varphi (z_2)$：
$${\mathcal{H}}_{x_1}(z_2)\le \varphi (z_2)\triangleq \frac{\mathcal{L}}{2}||z_2|{|}^2-\frac{\mathcal{L}}{2}||z_1|{|}^2+{\mathcal{H}}_{x_1}(z_1)+{\left[\nabla {\mathcal{H}}_{x_1}(z_1)-\mathcal{L}\cdot z_1\right]}^T(z_2-z_1)$$
再次观察$\varphi (z_2)$中与$z_2$相关的项(其中仅与$z_1$相关的项被视作常数)：

• $\begin{array}{r}\frac{\mathcal{L}}{2}||z_2|{|}^2\end{array}$是关于$z_2$的二次项，是凸函数；且二次项系数$\begin{array}{r}\frac{\mathcal{L}}{2}\ge 0\end{array}$，必然存在最小值；
• ${\left[\nabla {\mathcal{H}}_{x_1}(z_1)-\mathcal{L}\cdot z_1\right]}^T(z_2-z_1)$是关于$z_1$的一次函数，同样是凸函数。

最终通过保凸运算，能够确定$\varphi (z_2)$是一个凸二次函数。由于${\mathcal{H}}_{x_1}(z_2)\le \varphi (z_2)$，必然也小于$\varphi (z_2)$的最小值，也就是下界 inf ⁡ { ϕ ( z 2 ) } = min ⁡ ϕ ( z 2 ) \inf \{\phi(z_2)\} = \mathop{\min} \phi(z_2) inf{ϕ(z2​)}=minϕ(z2​)：
H x 1 ( z 2 ) ≤ inf ⁡ { ϕ ( z 2 ) } \mathcal H_{x_1}(z_2) \leq \inf \{\phi(z_2)\} Hx1​​(z2​)≤inf{ϕ(z2​)}
下面关于 inf ⁡ { ϕ ( z 2 ) } \inf\{\phi(z_2)\} inf{ϕ(z2​)}进行求解：

• 求解梯度$\nabla \varphi (z_2)$：
  $$\nabla \varphi (z_2)=\mathcal{L}\cdot z_2+\nabla {\mathcal{H}}_{x_1}(z_1)-\mathcal{L}\cdot z_1$$
• 令$\nabla \varphi (z_2)\triangleq 0$，有：
  也就是说：$\varphi (z_{2;min})=\min \varphi (z_2)$。
  $$z_{2;min}=z_1-\frac{\nabla {\mathcal{H}}_{x_1}(z_1)}{\mathcal{L}}$$
• 将$z_{2;min}$带回原式，得到$\min \varphi (z_2)$有：
  $$\varphi (z_{2;min})=\frac{\mathcal{L}}{2}||\frac{\mathcal{L}\cdot z_1-\nabla {\mathcal{H}}_{x_1}(z_1)}{\mathcal{L}}|{|}^2-\frac{\mathcal{L}}{2}||z_1|{|}^2+{\mathcal{H}}_{x_1}(z_1)+[\nabla {\mathcal{H}}_{x_1}(z_1)-\mathcal{L}\cdot z_1{]}^T\left[-\frac{\nabla {\mathcal{H}}_{x_1}(z_1)}{\mathcal{L}}\right]$$
• 很明显，只剩下了已知项$z_1$。整理有：
  • 提出公因式$\begin{array}{r}\frac{1}{2\mathcal{L}}[\mathcal{L}\cdot z_1-\nabla {\mathcal{H}}_{x_1}(z_1)]\end{array}$
  • 使用乘法分配律~
    ϕ ( z 2 ; m i n ) = 1 2 L ∣ ∣ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ∣ ∣ 2 − L 2 ∣ ∣ z 1 ∣ ∣ 2 + H x 1 ( z 1 ) + 1 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T ∇ H x 1 ( z 1 ) = 1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T { L ⋅ z 1 − ∇ H x 1 ( z 1 ) + 2 ∇ H x 1 ( z 1 ) } + h x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = 1 2 L [ L ⋅ z 1 − ∇ H x 1 ( z 1 ) ] T { L ⋅ z 1 + ∇ H x 1 ( z 1 ) } ⏟ 分配律 + h x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = 1 2 L [ L 2 ⋅ ∣ ∣ z 1 ∣ ∣ 2 − ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 ] + H x 1 ( z 1 ) − L 2 ∣ ∣ z 1 ∣ ∣ 2 = H x 1 ( z 1 ) − 1 2 L ∣ ∣ ∇ H x 1 ( z 1 ) ∣ ∣ 2 \begin{aligned} \phi(z_{2;min}) & = \frac{1}{2\mathcal L}||\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)||^2 - \frac{\mathcal L}{2}||z_1||^2 + \mathcal H_{x_1}(z_1) + \frac{1}{\mathcal L} [\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \nabla \mathcal H_{x_1}(z_1) \\ & = \frac{1}{2\mathcal L} [\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \left\{\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1) + 2 \nabla \mathcal H_{x_1}(z_1)\right\} + h_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \frac{1}{2\mathcal L} \underbrace{[\mathcal L \cdot z_1 - \nabla \mathcal H_{x_1}(z_1)]^T \left\{\mathcal L \cdot z_1 + \nabla \mathcal H_{x_1}(z_1) \right\}}_{分配律} + h_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \frac{1}{2\mathcal L} \left[\mathcal L^2 \cdot ||z_1||^2 - ||\nabla \mathcal H_{x_1}(z_1)||^2\right] + \mathcal H_{x_1}(z_1) - \frac{\mathcal L}{2}||z_1||^2 \\ & = \mathcal H_{x_1}(z_1) - \frac{1}{2\mathcal L}||\nabla \mathcal H_{x_1}(z_1)||^2 \end{aligned} ϕ(z2;min​)​=2L1​∣∣L⋅z1​−∇Hx1​​(z1​)∣∣2−2L​∣∣z1​∣∣2+Hx1​​(z1​)+L1​[L⋅z1​−∇Hx1​​(z1​)]T∇Hx1​​(z1​)=2L1​[L⋅z1​−∇Hx1​​(z1​)]T{L⋅z1​−∇Hx1​​(z1​)+2∇Hx1​​(z1​)}+hx1​​(z1​)−2L​∣∣z1​∣∣2=2L1​分配律 [L⋅z1​−∇Hx1​​(z1​)]T{L⋅z1​+∇Hx1​​(z1​)}​​+hx1​​(z1​)−2L​∣∣z1​∣∣2=2L1​[L2⋅∣∣z1​∣∣2−∣∣∇Hx1​​(z1​)∣∣2]+Hx1​​(z1​)−2L​∣∣z1​∣∣2=Hx1​​(z1​)−2L1​∣∣∇Hx1​​(z1​)∣∣2​

至此，我们找到了关于${\mathcal{H}}_{x_1}(z_2)$的二次上界：
$${\mathcal{H}}_{x_1}(z_2)\le {\mathcal{H}}_{x_1}(z_1)-\frac{1}{2\mathcal{L}}||\nabla {\mathcal{H}}_{x_1}(z_1)|{|}^2$$
在${\mathcal{H}}_{x_1}(\cdot )$函数的收敛过程中，其最小值${\mathcal{H}}_{x_1}^{\ast }$必然有：
通过数值解只能无限接近最小值。
$${\mathcal{H}}_{x_1}^{\ast }\le {\mathcal{H}}_{x_1}(z_2)\le {\mathcal{H}}_{x_1}(z_1)-\frac{1}{2\mathcal{L}}||\nabla {\mathcal{H}}_{x_1}(z_1)|{|}^2$$
因为${\mathcal{H}}_{x_1}(\cdot )$函数在$x_1$处取得最小值：${\mathcal{H}}_{x_1}(x_1)={\mathcal{H}}_{x_1}^{\ast }$，并且$z_1$与$x_1$定义域相同，不妨设：$z_1=x_2$，有：
$$\begin{array}{rl}& {\mathcal{H}}_{x_1}(x_1)\le {\mathcal{H}}_{x_1}(x_2)-\frac{1}{2\mathcal{L}}||\nabla {\mathcal{H}}_{x_1}(x_2)|{|}^2\\ \Rightarrow & {\mathcal{H}}_{x_1}(x_2)-{\mathcal{H}}_{x_1}(x_1)\ge \frac{1}{2\mathcal{L}}||\nabla {\mathcal{H}}_{x_1}(x_2)|{|}^2\end{array}$$
由于${\Delta }_1={\mathcal{H}}_{x_1}(x_2)-{\mathcal{H}}_{x_1}(x_1)$，因而最终有：
将$\nabla {\mathcal{H}}_{x_1}(\mathcal{Z}=x_2)=\nabla f(x_2)-\nabla f(x_1)$代入：
$$\begin{array}{rl}{\Delta }_1& \ge \frac{1}{2\mathcal{L}}||\nabla {\mathcal{H}}_{x_1}(x_2)|{|}^2\\ & =\frac{1}{2\mathcal{L}}||\nabla f(x_2)-\nabla f(x_1)|{|}^2\\ & =\frac{1}{2\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2\end{array}$$
当然，这仅仅证明了一半，我们同样需要针对${\Delta }_2$执行上述流程：
和上述流程完全相同，只不过可变参数由$x_1$变成了$x_2$,这里不再赘述。
Δ 2 = [ f ( x 1 ) − f ( x 2 ) ] − { [ ∇ f ( x 2 ) ] T x 1 − [ ∇ f ( x 2 ) ] T x 2 } = f ( x 1 ) − [ ∇ f ( x 2 ) ] T x 1 ⏟ 1 − { f ( x 2 ) − [ ∇ f ( x 2 ) ] T x 2 } ⏟ 2 = H x 2 ( x 1 ) − H x 2 ( x 2 ) \begin{aligned} \Delta_2 & = [f(x_1) - f(x_2)] - \left\{[\nabla f(x_2)]^T x_1 - [\nabla f(x_2)]^T x_2 \right\} \\ & = \underbrace{f(x_1) - [\nabla f(x_2)]^T x_1}_{1} - \underbrace{\{f(x_2) - [\nabla f(x_2)]^T x_2\}}_{2} \\ & = \mathcal H_{x_2}(x_1) - \mathcal H_{x_2}(x_2) \end{aligned} Δ2​​=[f(x1​)−f(x2​)]−{[∇f(x2​)]Tx1​−[∇f(x2​)]Tx2​}=1 f(x1​)−[∇f(x2​)]Tx1​​​−2 {f(x2​)−[∇f(x2​)]Tx2​}​​=Hx2​​(x1​)−Hx2​​(x2​)​
最终也可以得到一个类似结果：
$${\Delta }_2\ge \frac{1}{2\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2$$
从而最终可得：
$$\begin{array}{rl}{\Delta }_1+{\Delta }_2& \ge 2\cdot \frac{1}{2\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2\\ & =\frac{1}{\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2\end{array}$$
即：
$$[\nabla f(x_1)-\nabla f(x_2){]}^T(x_1-x_2)\ge \frac{1}{\mathcal{L}}||\nabla f(x_1)-\nabla f(x_2)|{|}^2$$
即梯度函数$\nabla f(\cdot )$具备余强制性，证毕。