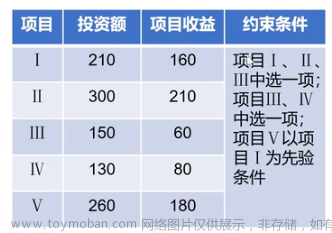
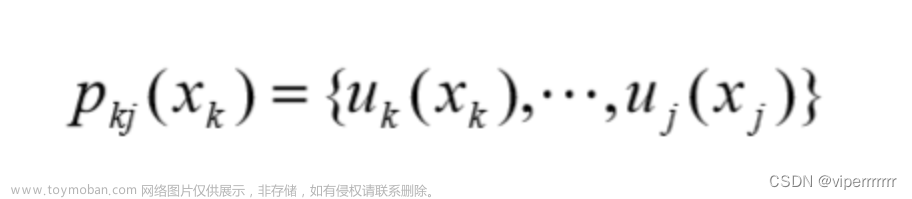1. 核心原理简介
1.1 三个重要概念
(1) 正负偏差变量
【衡量每个目标的完成情况】
设 为第i个目标函数的实际值;
设 表示 的目标值
- 正偏差变量
【表示实际值超过目标值的部分】
- 负偏差变量 【表示实际值未达到目标值的部分】
实例说明:
目标函数实际值 目标值 正偏差变量
负偏差变量
意义 收入50万 不少于60万 0 10 未到达还有10万 收入70万 10 0 超出10万
(2) 绝对约束与目标约束
- 绝对约束
【必须要满足的条件】
- 目标约束
【允许有偏差→利用正负偏差变量】
实例说明:【含有“尽可能”、“尽量”等关键词】
尽可能使利润不低于56万
(3)优先因子
【类似“权重”】
给每一个目标一个优先因子P,仅仅是确定各目标的求解次序
1.2 序贯算法
【将之前的单目标最优解变成下一个目标的约束条件,然后迭代这个过程】
1.根据模型中各个目标的优先级(优先因子),确定各目标的求解次序
2.求第一级单目标规划的最优值(注意要先给最优解附一个初值)
3.以第一 级单目标等于最优值为新的约束条件,求第二级目标最优值记为
4.依次递推,直到所有目标都求完或不存在可行解为止
2. 实例建模过程
2.1 实例
某工厂生产产品1和产品2,有关数据如下,请给出方案,设计每天生产产品1、2各多少时,满足下面的要求:
现在的要求是:
2.2 建模过程
(1)分析问题(翻译成数学语言)
- 根据原材料拥有量
- 根据生产能力
- 根据具体要求(因为带有“尽可能”关键词,为目标约束)
(2)引入正负变差变量
【以上不等式变形顺序对应】
- 第一个不等式:因为是≤,所以要求正偏差变量要最小
- 第二个不等式:因为是=,所以要求正偏差和负偏差都要小,所以求和要最小
- 第三个不等式:因为是≥,所以要求负偏差变量要最小
所以得到目标函数:
P仅仅是优先因子,仅仅决定后面多目标求解顺序,而不是真正意义上的权重值
根据1中原理介绍偏差变量,目标函数看似没有包含变量x,实则每一个偏差变量都要利用x计算
(3)模型总结
- 目标函数:
- 约束条件:
“多退少补”原则【将目标约束中的不等式变成等式】
表示:减去“超过”的,加上“未达到”
3. Matlab实现
3.1 代码
clc,clear
%初始化优化问题框架
%创建优化变量
%%2个产品【用x表示】【最小值=0】
x = optimvar('x',2,'LowerBound',0);
%%3个目标函数的正偏差变量 【最小值=0】
dp = optimvar('dp',3,'LowerBound',0);
%%3个目标函数的负偏差变量 【最小值=0】
dm = optimvar('dm',3,'LowerBound',0);
%创建优化问题对象
p = optimproblem('ObjectiveSense','min');
%设置约束条件
%%设置绝对约束
p.Constraints.cons1 = (2*x(1)+x(2)<=11);
%%设置3个目标约束
p.Constraints.cons2 = [x(1)-x(2)-dp(1)+dm(1)==0
x(1)+2*x(2)-dp(2)+dm(2)==10
8*x(1)+10*x(2)-dp(3)+dm(3)==56];
%设置目标函数
obj = [dp(1);dm(2)+dp(2);dm(3)];
% 单级目标函数的最优值goal,初始设为足够大的数
% 非常宽松的约束就等于没有约束,确保第一级的正常运算
goal=100000*ones(3,1);
%序贯算法(迭代最优)
for i=1:3
% 重要:更新上一级的最优值,作为该级的约束条件;
p.Constraints.cons3=[obj<=goal];
p.Objective = obj(i);
%求解【 针对优化问题使用solve,会自动选择求解方式】
[sx,fval] = solve(p);
%【下面两行可注释】只是展示每一次迭代结果
fprintf('第%d级目标求解为:\n',i)
fval, xx=sx.x, sdm=sx.dm, sdp=sx.dp
%sx类似于python中创建的类【这里指优化类】
%x(最后得到的优化方案)、dm(负偏差变量)、dp(正偏差变量)为3个sx下的对象
goal(i) = fval;
end3.2 结果展示

表示:每天应生产产品一2件,产品二4件
4. 总结
(1)问题函数optimproblem【用来创建优化问题】
prob=optimproblem('ObjectiveSense','max');
ObjectiveSense是目标类型,后面跟的‘max’为求最大优化
默认为求min
(2) 求解函数`optimvar`【一种类似于赋值的函数】
x=optimvar('x',1,2,'TYPE','integer','LowerBound',0,'UpperBound',inf);
第一个‘x’里面是变量名,后面 1 2 为变量的行 列
‘TYPE’,后面定义的是该函数所属类型,比如说integer整数型,double双精度型号等
‘LowerBound'下界;'UpperBound'上界
(3) 设置约束条件prob.Constraints.cons1
p.Constraints.cons1 = ( 2*x(1)+x(2)<=11 )
p.Constraints.cons2=[x(1)-x(2)+dm(1)-dp(1)==0
x(1)+2*x(2)+dm(2)-dp(2)==10
8*x(1)+10*x(2)+dm(3)-dp(3)==56];-
p为优化问题创建的对象
(4) 设置目标函数pro.Objective
obj=[dp(1); dm(2)+dp(2); dm(3)];
p.Objective=obj(i);-
p为优化问题创建的对象
(5) sovle函数求解
[sx,fval]=solve(p);
p为优化问题创建的对象
sx为最优值变量(理想)文章来源:https://www.toymoban.com/news/detail-657514.html
fval为在最优变量下的目标函数值文章来源地址https://www.toymoban.com/news/detail-657514.html
到了这里,关于数学建模|多目标规划+序贯算法|简要原理+实例matalb代码实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!