Java进阶篇--数据结构-Toy模板网

这篇具有很好参考价值的文章主要介绍了Java进阶篇--数据结构。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

#我的编程语言学习笔记#

一.数组（Array）：

1.1 特点：

1.2 基本操作：

1.3 使用数组的好处包括：

1.4 数组也有一些限制：

二.集合框架（Collections Framework）：

2.1 列表（List）：

2.1.1 数组列表（ArrayList）：

扩展知识：

方法：

ArrayList的遍历方式

ArrayList使用泛型

Arrays工具类

2.1.2 链表（LinkedList）：

常用方法：

2.1.3 使用选择：

2.1.4 示例代码：

2.2 集（Set）：

2.2.1 哈希集（HashSet）：

基本类型对应的包装类表如下：

HashSet的常用方法包括：

2.2.2 树集（TreeSet）：

TreeSet的常用方法包括：

2.2.3 使用选择：

2.2.4 示例代码：

2.3 映射（Map）：

2.3.1 哈希映射（HashMap）：

2.3.2 树映射（TreeMap）：

2.3.3 使用选择

2.3.4 示例代码

三.栈（Stack）和队列（Queue）：

3.1方法

3.2示例代码

四.树（Tree）：

4.1 二叉树（Binary Tree）：

4.2二叉搜索树（Binary Search Tree）：

4.3 操作方法

4.4 树的遍历

4.4.1树的遍历包括两种主要方式：

4.4.2 树的两种基本遍历方式：

4.5 示例代码

五.图（Graph）：

5.1 有向图（Directed Graph）：

5.2 无向图（Undirected Graph）：

5.3 使用选择

5.4 示例代码

六.堆（Heap）：

6.1 最大堆（Max Heap）：

6.2 最小堆（Min Heap）：

6.3 示例代码

七.链表（LinkedList）：

7.1 单向链表：

7.2 双向链表：

7.3 使用选择

7.4 常用方法

7.5 示例代码

八.MAP：

8.1 常见的Map实现类：

8.2 常用的方法

8.3 使用选择

8.4 示例代码

Java 提供了多种数据结构来有效地组织和处理数据。以下是一些常见的 Java 数据结构：

一.数组（Array）：

数组（Array）是一种线性数据结构，用于存储固定大小的相同类型元素的连续序列，可以通过索引快速访问和修改元素。。在 Java 中，数组可以包含基本类型（如 int、double、char 等）或引用类型（如对象、字符串等）的元素。

1.1 特点：

元素类型必须相同，即数组是同一类型的项的集合。
长度固定，在创建数组时需要指定大小，后续无法改变。
内存中分配连续的空间，元素之间存储紧密，通过索引快速访问和修改元素。

1.2 基本操作：

初始化：创建一个数组，并为其赋初值。
遍历：使用循环遍历数组中的每个元素。
打印：将数组中的元素依次输出。
最大值：遍历数组，通过比较找到数组中的最大值。
最大值下标：遍历数组，记录当前最大值的下标。
使用增强for循环（foreach）：对于数组中的每个元素，可以使用增强for循环进行遍历并执行相应的操作。
复制数组有三种方法：

遍历原数组，逐个复制到新数组。
使用System.arraycopy()方法进行数组复制。
使用数组的clone()方法复制数组。

线性查找：：从数组的第一个元素开始逐个比较，直到找到目标元素或遍历完整个数组。时间复杂度为O(n)，其中n为数组长度。
二分查找：要求在已排序的数组中进行查找。首先确定数组的中间元素，将目标值与中间元素进行比较，若相等则返回该位置，若小于中间元素，则在左半部分继续查找，若大于中间元素，则在右半部分继续查找。重复以上步骤，直到找到目标值或查找范围为空。时间复杂度为O(logn)，其中n为数组长度。
选择排序：每次遍历找到当前范围内的最小（或最大）元素，并将其放置在已排序的部分的末尾。通过不断选择最小（或最大）的元素，逐步完成整个数组的排序。注意，选择排序的时间复杂度为O(n^2)，其中n为数组的长度。虽然简单易实现，但对于较大规模的数据可能效率较低。

以下的Java代码示例，包含数组的初始化、遍历、打印、最大值、最大值下标、使用增强for循环遍历、复制数组以及线性查找、二分查找和选择排序算法的实现。

import java.util.Arrays;

public class myClass {
    public static void main(String[] args) {
        // 初始化数组
        int[] arr = {5, 3, 9, 1, 7};

        // 遍历数组
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();

        // 打印数组
        System.out.println(Arrays.toString(arr));

        // 最大值
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        System.out.println("最大值：" + max);

        // 最大值下标
        int maxIndex = 0;
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > arr[maxIndex]) {
                maxIndex = i;
            }
        }
        System.out.println("最大值下标：" + maxIndex);

        // 使用增强for循环遍历
        for (int num : arr) {
            System.out.print(num + " ");
        }
        System.out.println();

        // 复制数组方法一（遍历原数组，逐个复制到新数组）
        int[] copyArr1 = new int[arr.length];
        for (int i = 0; i < arr.length; i++) {
            copyArr1[i] = arr[i];
        }

        // 复制数组方法二（使用System.arraycopy()方法）
        int[] copyArr2 = new int[arr.length];
        System.arraycopy(arr, 0, copyArr2, 0, arr.length);

        // 复制数组方法三（使用数组的clone()方法）
        int[] copyArr3 = arr.clone();

        System.out.println("复制后的数组：" + Arrays.toString(copyArr3));

        // 线性查找
        int target = 9;
        int linearSearchIndex = -1;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == target) {
                linearSearchIndex = i;
                break;
            }
        }
        System.out.println("线性查找：" + (linearSearchIndex != -1 ? linearSearchIndex : "未找到"));

        // 二分查找（前提是数组必须有序）
        Arrays.sort(arr); // 先排序
        int binarySearchIndex = Arrays.binarySearch(arr, target);
        System.out.println("二分查找：" + (binarySearchIndex >= 0 ? binarySearchIndex : "未找到"));

        // 选择排序
        selectionSort(arr);
        System.out.println("选择排序后的数组：" + Arrays.toString(arr));
    }

    // 选择排序算法实现
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            if (minIndex != i) {
                int temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }
    }
}

运行结果：

5 3 9 1 7 
[5, 3, 9, 1, 7]
最大值：9
最大值下标：2
5 3 9 1 7 
复制后的数组：[5, 3, 9, 1, 7]
线性查找：2
二分查找：4
选择排序后的数组：[1, 3, 5, 7, 9]

1.3 使用数组的好处包括：

快速随机访问：由于元素在内存中连续存储，所以可以通过索引快速定位和访问元素。
内存效率：数组在创建时需要指定长度，适用于已知固定数量的元素存储场景，不需要额外的指针或链接信息。
数组操作简单：Java 提供了一些便利的方法和属性，使得数组的操作更加简单和高效。

1.4 数组也有一些限制：

长度固定：一旦创建，长度无法改变，需要事先确定好所需的元素个数。
内存浪费：如果数组长度过大或未充分利用，会造成内存浪费。
数据类型：数组只能存储一种类型的数据；
插入和删除困难：在数组中插入或删除元素可能需要移动其他元素，开销较大。

二.集合框架（Collections Framework）：

提供了一系列接口和类，用于存储和操作对象的集合。常用的集合类包括：

2.1 列表（List）：

有序、可重复的集合，例如 ArrayList、LinkedList。

2.1.1 数组列表（ArrayList）：

ArrayList是基于数组实现的动态数组，内部通过数组来存储元素。
它可以自动扩容以适应元素的增加
它支持随机访问元素，即可以通过索引快速访问指定位置的元素。
数组列表适用于频繁读取和随机访问元素的场景，因为它内部使用数组存储，可以根据索引直接计算出元素的内存地址。
ArrayList实现了List接口，继承了AbstractList类，并且还实现了RandomAccess（随机访问）、Cloneable（克隆）和Serializable（可序列化）这些接口。
与Vector不同，ArrayList不是线程安全的。因此，在单线程环境下建议使用ArrayList，在多线程环境下可以选择Vector或CopyOnWriteArrayList。

扩展知识：

Vector是Java中的一个旧的类，它与ArrayList具有相似的用法，但在性能和使用上存在一些差异。虽然Vector是线程安全的，但在大多数情况下，推荐使用更现代的替代方案。

一个常见的替代方案是使用Collections工具类提供的synchronizedList方法，该方法可以将ArrayList转换为线程安全的List。以下是示例代码：

List<String> lst = new ArrayList<>();
// 往lst中添加元素

List<String> synList = Collections.synchronizedList(lst);

通过将原始的ArrayList通过synchronizedList方法包装，我们可以获得一个在并发环境下安全使用的List。

需要注意的是，在大多数情况下，如果不需要线程安全的特性，推荐使用ArrayList而不是Vector，因为ArrayList在性能上通常更优。只有在确实需要线程安全时，才会考虑使用Vector或通过Collections工具类获得线程安全的List。

方法：

Collection相关方法：

这些方法属于Collection类的一部分，可以被List和Set等子类继承并使用。以下是一些常见的Collection类方法：

boolean add(E element)：向集合中添加一个元素。
boolean addAll(Collection<? extends E> collection)：将一个集合中的所有元素添加到当前集合中。
void clear()：清空集合中的所有元素。
boolean contains(Object object)：判断集合是否包含指定对象。
boolean containsAll(Collection<?> collection)：判断集合是否包含给定集合中的所有元素。
boolean isEmpty()：判断集合是否为空。
Iterator<E> iterator()：返回一个用于迭代集合元素的迭代器。
boolean remove(Object object)：从集合中移除指定的对象。
boolean removeAll(Collection<?> collection)：从集合中移除给定集合中的所有元素。
boolean retainAll(Collection<?> collection)：仅保留集合中在给定集合中出现的元素，移除其他元素。
int size()：返回集合中的元素个数。
Object[] toArray()：将集合转化为数组。
<T> T[] toArray(T[] array)：将集合转化为指定类型的数组。

List接口：

List是Collection接口的子接口，拥有Collection所有方法外，还有一些对索引操作的方法。

void add(int index, E element)：在索引index处插入元素element。
boolean addAll(int index, Collection<? extends E> c)：将集合c中的所有元素插入到索引index处。
E remove(int index)：移除并返回索引index处的元素。
int indexOf(Object o)：返回对象o在ArrayList中第一次出现的索引。
int lastIndexOf(Object o)：返回对象o在ArrayList中最后一次出现的索引。
E set(int index, E element)：将索引index处的元素替换为新的element对象，并返回被替换的旧元素。
E get(int index)：返回索引index处的元素。
List<E> subList(int fromIndex, int toIndex)：返回从索引fromIndex（包含）到索引toIndex（不包含）的子列表。
void sort(Comparator<? super E> c)：根据指定的Comparator对ArrayList中的元素进行排序。
void replaceAll(UnaryOperator<E> operator)：使用指定的计算规则operator重新设置ArrayList的所有元素。
ListIterator<E> listIterator()：返回一个ListIterator对象，该接口继承了Iterator接口，在Iterator接口基础上增加了以下方法，允许向前迭代并添加元素。
bookean hasPrevious()：返回迭代器关联的集合是否还有上一个元素；
E previous();：返回迭代器上一个元素；
void add(E e);：在指定位置插入元素；

更多 API 方法可以查看：ArrayList

ArrayList的遍历方式

使用for循环和索引：

for (int i = 0; i < arrayList.size(); i++) {
    E element = arrayList.get(i);
    // 处理元素
}

使用for-each循环：

for (E element : arrayList) {
    // 处理元素
}

使用迭代器（Iterator）进行遍历：

Iterator<E> iterator = arrayList.iterator();
while (iterator.hasNext()) {
    E element = iterator.next();
    // 处理元素
}

ArrayList<E>使用泛型

泛型数据类型，用于设置 objectName（对象名）的数据类型，只能为引用数据类型。

对于ArrayList的泛型使用，可以通过在定义ArrayList时指定泛型类型来确保集合中只能存储指定类型的元素。例如：

ArrayList<String> stringList = new ArrayList<>();
stringList.add("Hello");
stringList.add("World");
// 只能添加String类型的元素

String element = stringList.get(0);
System.out.println(element);  // 输出: Hello

通过使用泛型，可以提供类型安全，并且在编译期间就能够捕获类型不匹配的错误。

Arrays工具类

Arrays工具类是Java提供的用于操作数组的工具类，以下是一些常用的方法：

boolean equals(a, b)：比较两个数组是否相等。
void fill(array, value)：将指定的值填充到数组中的所有元素。
void sort(array)：对数组进行排序。
int binarySearch(array, key)：在已排序的数组中使用二分查找来查找指定的元素。
void arraycopy(src, srcPos, dest, destPos, length)：将源数组中的某个范围的元素复制到目标数组的指定位置。

2.1.2 链表（LinkedList）：

LinkedList是基于链表实现的双向链表，内部通过节点（Node）来存储元素并连接起来。
节点中包含了当前元素的值，以及指向前一个节点和后一个节点的引用。
链表支持快速插入和删除操作，因为只需要修改节点的引用关系即可，不涉及移动其他元素。
链表适用于频繁插入和删除元素的场景，因为在链表中插入和删除元素的开销相对较小。
由于链表的存储方式不同于数组，因此在访问某个位置的元素时需要遍历链表，因此随机访问的效率较低。

常用方法：

void addFirst(E element)：在链表的开头插入元素。
void addLast(E element)：在链表的末尾插入元素。
E getFirst()：获取链表中的第一个元素。
E getLast()：获取链表中的最后一个元素。
E removeFirst()：移除并返回链表中的第一个元素。
E removeLast()：移除并返回链表中的最后一个元素。
boolean contains(Object element)：判断链表是否包含指定元素。
int size()：返回链表中的元素个数。
void clear()：清空链表中的所有元素。

更多 API 方法可以查看：LinkedList

2.1.3 使用选择：

根据具体需求，选择ArrayList还是LinkedList有以下一些考虑因素：

如果需要频繁读取和随机访问元素，可以选择ArrayList。
如果需要频繁插入和删除元素，尤其是在列表的中间位置，可以选择LinkedList。
如果对内存空间的利用比较敏感，LinkedList可能会占用更多的内存，而ArrayList使用的内存通常较为紧凑。

总的来说，ArrayList适用于读取和随机访问操作更多的场景，而LinkedList适用于插入和删除操作更频繁的场景。

2.1.4 示例代码：

下面一个简单的示例代码，展示了如何使用ArrayList和LinkedList进行基本操作：

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class ListExample {
    public static void main(String[] args) {
        // 使用ArrayList
        List<String> arrayList = new ArrayList<>();

        // 添加元素
        arrayList.add("Apple");
        arrayList.add("Banana");
        arrayList.add("Orange");

        // 获取元素
        String firstElement = arrayList.get(0);
        System.out.println("ArrayList中第一个元素：" + firstElement);

        // 遍历元素
        System.out.println("ArrayList的元素：");
        for (String element : arrayList) {
            System.out.println(element);
        }

        // 删除元素
        arrayList.remove("Banana");

        // 使用LinkedList
        List<Integer> linkedList = new LinkedList<>();

        // 添加元素
        linkedList.add(10);
        linkedList.add(20);
        linkedList.add(30);

        // 获取元素
        int lastElement = linkedList.get(linkedList.size() - 1);
        System.out.println("LinkedList中最后一个元素：" + lastElement);

        // 遍历元素
        System.out.println("LinkedList的元素：");
        for (int element : linkedList) {
            System.out.println(element);
        }

        // 删除元素
        linkedList.remove(0);
    }
}

运行结果：

ArrayList中第一个元素：Apple
ArrayList的元素：
Apple
Banana
Orange
LinkedList中最后一个元素：30
LinkedList的元素：
10
20
30

2.2 集（Set）：

集是一种无序的集合，不允许重复元素，例如 HashSet、TreeSet。

2.2.1 哈希集（HashSet）：

HashSet是基于哈希表实现的集合，具有快速查找性能。
哈希集不保证元素的顺序，且不允许重复元素。如果试图插入重复元素，插入操作将被忽略。
它还继承了Set接口和Collection接口的其他方法
HashSet允许存储null元素。
添加、删除和查找元素的平均时间复杂度为O(1)。

HashSet 中的元素实际上是对象，一些常见的基本类型可以使用它的包装类。

基本类型对应的包装类表如下：

基本类型	引用类型
boolean	Boolean
byte	Byte
short	Short
int	Integer
long	Long
float	Float
double	Double
char	Character

HashSet的常用方法包括：

boolean add(E element)：向集合中添加指定元素，如果元素已经存在，则返回false。
boolean remove(Object element)：从集合中移除指定元素，如果元素存在并成功移除，则返回true。
boolean contains(Object element)：检查集合中是否包含指定元素，如果包含则返回true。
int size()：返回集合中元素的数量。
void clear()：清空集合中的所有元素。

更多 API 方法可以查看：HashSet

2.2.2 树集（TreeSet）：

TreeSet是基于红黑树（自平衡二叉搜索树）实现的有序集合。
树集中的元素按照自然顺序或自定义比较器进行排序，默认情况下按照元素的自然排序方式进行排序。
它还继承了Set接口和Collection接口的其他方法
树集不允许插入null元素。
插入、删除和查找元素的时间复杂度为O(log N)，其中N为树集中的元素个数。

TreeSet的常用方法包括：

boolean add(E element)：向集合中添加指定元素，如果元素已经存在，则返回false。
boolean remove(Object element)：从集合中移除指定元素，如果元素存在并成功移除，则返回true。
boolean contains(Object element)：检查集合中是否包含指定元素，如果包含则返回true。
int size()：返回集合中元素的数量。
void clear()：清空集合中的所有元素。
E first()：返回集合中的第一个（最小）元素。
E last()：返回集合中的最后一个（最大）元素。
Iterator<E> iterator()：返回在此集合上进行迭代的迭代器。

2.2.3 使用选择：

使用HashSet时，你可以快速添加、删除和查找元素，并且元素的顺序可能不同。
如果你希望元素有一定的顺序，你可以使用TreeSet，它会根据元素的排序规则保持元素的有序性。

2.2.4 示例代码：

下面一个简单的示例代码，展示了如何使用HashSet和TreeSet进行基本操作：

import java.util.HashSet;// 引入 HashSet 类
import java.util.TreeSet;// 引入 TreeSet 类

public class myClass {
    public static void main(String[] args) {
        // 使用HashSet
        HashSet<String> hashSet = new HashSet<>();

        // 添加元素
        hashSet.add("Apple");
        hashSet.add("Banana");
        hashSet.add("Orange");
        hashSet.add("Grape");

        // 输出集合中的元素
        System.out.println("HashSet:");
        for (String fruit : hashSet) {
            System.out.println(fruit);
        }

        // 检查元素是否存在
        System.out.println("HashSet contains 'Apple': " + hashSet.contains("Apple")); // true

        // 删除元素
        hashSet.remove("Orange");

        // 输出修改后的集合
        System.out.println("HashSet after removal:");
        for (String fruit : hashSet) {
            System.out.println(fruit);
        }

        // 使用TreeSet
        TreeSet<Integer> treeSet = new TreeSet<>();

        // 添加元素
        treeSet.add(5);
        treeSet.add(10);
        treeSet.add(3);
        treeSet.add(8);

        // 输出集合中的元素
        System.out.println("TreeSet:");
        for (int num : treeSet) {
            System.out.println(num);
        }

        // 获取最小元素和最大元素
        System.out.println("Min element: " + treeSet.first()); // 3
        System.out.println("Max element: " + treeSet.last()); // 10
    }
}

运行结果：

HashSet:
Apple
Grape
Orange
Banana
HashSet contains 'Apple': true
HashSet after removal:
Apple
Grape
Banana
TreeSet:
3
5
8
10
Min element: 3
Max element: 10

2.3 映射（Map）：

由键值对组成的集合，每个键唯一，例如 HashMap、TreeMap。

2.3.1 哈希映射（HashMap）：

它是基于哈希表实现的映射结构。
HashMap是一个散列表，它存储的内容是键值对(key-value)映射，键不可重复，值可以重复。
底层哈希表，线程不安全，允许key为null，value也可以为null
HashMap使用键的哈希码来确定存储位置，实现了 Map 接口，通过键快速查找值。
它具有较快的插入和查找操作，但不保证元素的顺序。

常用方法：

put(key, value): 将键值对插入到哈希映射中。
get(key): 根据键获取对应的值。
containsKey(key): 检查哈希映射中是否包含指定的键。
remove(key): 移除哈希映射中指定键的键值对。
size(): 返回哈希映射中键值对的数量。

更多 API 方法可以查看：HashMap

2.3.2 树映射（TreeMap）：

它是基于红黑树实现的有序映射结构。
TreeMap将键按照自然顺序或通过自定义的比较器进行排序，并在内部维护一个有序的键值对集合。因此，可以根据键的顺序快速检索、遍历和范围查找元素。

常用方法：

put(key, value): 将键值对插入到树映射中。
get(key): 根据键获取对应的值。
containsKey(key): 检查树映射中是否包含指定的键。
remove(key): 移除树映射中指定键的键值对。
size(): 返回树映射中键值对的数量。
firstKey(): 返回树映射中最小的键。
lastKey(): 返回树映射中最大的键。
subMap(fromKey, toKey): 返回树映射中键的一个子集，范围从 fromKey（包括）到 toKey（不包括）。

除了上述方法，哈希映射和树映射还提供了其他一些类似的方法，如获取所有键的集合、清空映射等。具体的方法使用可以参考Java的官方文档或相关教程。

2.3.3 使用选择

这两种映射都是非常常用的数据结构，在不同的场景下使用。

HashMap适用于需要快速查找和插入元素的情况，并且不关心元素的顺序。
TreeMap适用于需要有序性的场景，可以按照键的顺序进行操作和遍历，在维护有序性的同时支持各种基本操作。

2.3.4 示例代码

下面一个简单的示例代码，展示了如何使用HashMap和TreeMap进行基本操作：

import java.util.HashMap;
import java.util.Map;
import java.util.TreeMap;

public class myClass {
    public static void main(String[] args) {
        // 使用HashMap
        Map<String, Integer> hashMap = new HashMap<>();

        // 添加键值对到HashMap
        hashMap.put("Apple", 1);
        hashMap.put("Banana", 2);
        hashMap.put("Orange", 3);

        // 获取指定键的值
        int appleValue = hashMap.get("Apple");
        System.out.println("Apple的值为：" + appleValue);

        // 检查HashMap是否包含指定键
        boolean containsKey = hashMap.containsKey("Banana");
        System.out.println("HashMap是否包含Banana：" + containsKey);

        // 移除指定键的键值对
        hashMap.remove("Orange");

        // 遍历HashMap的键值对
        for (String key : hashMap.keySet()) {
            int value = hashMap.get(key);
            System.out.println("键：" + key + "，值：" + value);
        }

        System.out.println("----------------------");

        // 使用TreeMap
        Map<String, Integer> treeMap = new TreeMap<>();

        // 添加键值对到TreeMap
        treeMap.put("Apple", 1);
        treeMap.put("Banana", 2);
        treeMap.put("Orange", 3);

        // 获取最小的键
        String firstKey = ((TreeMap<String, Integer>) treeMap).firstKey();
        System.out.println("最小的键：" + firstKey);

        // 获取最大的键
        String lastKey = ((TreeMap<String, Integer>) treeMap).lastKey();
        System.out.println("最大的键：" + lastKey);

        // 遍历TreeMap的键值对
        for (String key : treeMap.keySet()) {
            int value = treeMap.get(key);
            System.out.println("键：" + key + "，值：" + value);
        }
    }
}

运行结果：

Apple的值为：1
HashMap是否包含Banana：true
键：Apple，值：1
键：Banana，值：2
----------------------
最小的键：Apple
最大的键：Orange
键：Apple，值：1
键：Banana，值：2
键：Orange，值：3

三.栈（Stack）和队列（Queue）：

栈是一种后进先出（LIFO）的数据结构，常用操作有入栈和出栈；队列是一种先进先出（FIFO）的数据结构，常用操作有入队和出队。Java 提供了 Stack 类和 Queue 接口，并有相关实现类如 LinkedList。

栈（Stack）：是一种后进先出（LIFO）的数据结构，只允许在栈顶进行插入（入栈）和删除（出栈）操作。相当于把元素放在一个类似于竖起的桶中，每次插入和删除只能在桶的顶部进行。
队列（Queue）：是一种先进先出（FIFO）的数据结构，从队尾插入元素（入队），从队头删除元素（出队）。可以理解为排队，先进来的人先出去。

在Java中，可以使用Stack类表示栈，它是Vector的子类。而Queue接口是Java集合框架的一部分，它定义了队列的基本操作，如入队、出队、获取队头元素等。Java提供了多个Queue接口的实现类，其中常用的是LinkedList，它既实现了List接口，又实现了Deque接口，可以作为队列或双端队列使用。

3.1方法

Stack的常用方法包括：

push(element)：将元素压入栈顶。
pop()：弹出并返回栈顶的元素。
peek()：返回栈顶的元素，但不会将其从栈中移除。
isEmpty()：判断栈是否为空。
size()：返回栈中元素的个数。

Queue的常用方法包括：

add(element)：将元素添加到队尾。
offer(element)：将元素添加到队尾，并返回是否成功。
remove()：移除并返回队头的元素，如果队列为空则会直接抛出 NoSuchElementException 异常。
poll()：移除并返回队头的元素，如果队列为空则返回null。
peek()：返回队头的元素，但不会将其从队列中移除。
element()：返回队头的元素，如果队列为空则抛出异常。
isEmpty()：判断队列是否为空。
size()：返回队列中元素的个数。

3.2示例代码

下面一个简单的示例代码，展示了如何使用Stack和Queue进行基本操作：

import java.util.Stack;
import java.util.LinkedList;
import java.util.Queue;

public class myClass {
    public static void main(String[] args) {
        // 使用Stack
        Stack<Integer> stack = new Stack<>();

        // 入栈操作
        stack.push(1);
        stack.push(2);
        stack.push(3);

        // 出栈操作
        int poppedElement = stack.pop();
        System.out.println("出栈元素：" + poppedElement);

        // 获取栈顶元素
        int topElement = stack.peek();
        System.out.println("栈顶元素：" + topElement);

        // 判断栈是否为空
        boolean empty = stack.isEmpty();
        System.out.println("栈是否为空：" + empty);

        System.out.println("----------------------");

        // 使用Queue
        Queue<String> queue = new LinkedList<>();

        // 入队操作
        queue.offer("Apple");
        queue.offer("Banana");
        queue.offer("Orange");

        // 出队操作
        String polledElement = queue.poll();
        System.out.println("出队元素：" + polledElement);

        // 获取队头元素
        String peekedElement = queue.peek();
        System.out.println("队头元素：" + peekedElement);

        // 判断队列是否为空
        boolean emptyQueue = queue.isEmpty();
        System.out.println("队列是否为空：" + emptyQueue);
    }
}

运行结果：

出栈元素：3
栈顶元素：2
栈是否为空：false
----------------------
出队元素：Apple
队头元素：Banana
队列是否为空：false

四.树（Tree）：

树是一种非线性的数据结构，由节点和边组成，用于表示具有层级关系的数据结构。常见的树结构包括二叉树、平衡树、红黑树等。Java 提供了 TreeSet 和 TreeMap 来实现树结构。

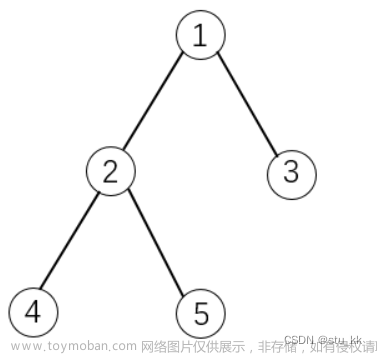
4.1 二叉树（Binary Tree）：

是一种特殊的树结构，每个节点最多有两个子节点：左子节点和右子节点。一个节点可以没有子节点，也可以只有一个子节点。

4.2二叉搜索树（Binary Search Tree）：

也称为二叉查找树或排序二叉树，是一种特殊的二叉树。它具有以下性质：

对于任意节点，其左子树上的所有节点的值都小于该节点的值。
对于任意节点，其右子树上的所有节点的值都大于该节点的值。
左子树和右子树都必须是二叉搜索树。

由于二叉搜索树的性质，我们可以利用它来高效地进行查找、插入和删除操作。对于任意节点，其左子树的节点值都小于该节点，因此在查找、插入或删除时，可以通过比较节点的值，有选择性地在左子树或右子树中进行操作，从而提高效率。

Java中可以使用TreeSet和TreeMap来实现二叉搜索树。它们基于红黑树（Red-Black Tree）实现，红黑树是一种自平衡的二叉搜索树，保持了良好的平衡性能。

TreeSet是一个基于红黑树实现的有序集合，它存储的元素按照自然顺序或者指定的比较器进行排序，并且不允许出现重复元素。
TreeMap是一个基于红黑树实现的有序映射，它存储键值对，并按照键的自然顺序或者指定的比较器进行排序。与TreeSet类似，TreeMap也不允许出现重复的键。

通过使用TreeSet和TreeMap，我们可以方便地操作二叉搜索树的相关操作，如插入、删除、查找等，并保持元素的有序性。

4.3 操作方法

创建树IntTree(&T)：创建1个空树T。
销毁树DestroyTree(&T)
构造树CreatTree(&T，deinition)
置空树ClearTree(&T):将树T置为空树。
判空树TreeEmpty(T)
求树的深度TreeDepth(T)
获得树根Root(T)
获取结点Value(T，cur_e，&e)：将树中结点cur_e存入e单元中。
数据赋值Assign(T，cur_e，value)：将结点value，赋值于树T的结点cur_e中。
获得双亲Parent(T，cur_e)：返回树T中结点cur_e的双亲结点。
获得最左孩子LeftChild(T，cur_e)：返回树T中结点cur_e的最左孩子。
获得右兄弟RightSibling(T，cur_e)：返回树T中结点cur_e的右兄弟。
插入子树InsertChild(&T，&p，i，c)：将树c插入到树T中p指向结点的第i个子树之前。
删除子树DeleteChild(&T，&p，i)：删除树T中p指向结点的第i个子树。
遍历树TraverseTree(T，visit())

4.4 树的遍历

4.4.1树的遍历包括两种主要方式：

深度优先遍历（DFS）：
1. 先序遍历（Preorder）：根节点 -> 左子树 -> 右子树
2. 中序遍历（Inorder）：左子树 -> 根节点 -> 右子树
3. 后序遍历（Postorder）：左子树 -> 右子树 -> 根节点
广度优先遍历（BFS）：从根节点开始，按层级顺序逐层遍历树的节点，从左到右依次访问每个节点。

无论是深度优先遍历还是广度优先遍历，都有各自的应用场景。可以根据具体需求选择适合的遍历方式来处理树中的节点。

4.4.2 树的两种基本遍历方式：

先序遍历（Preorder traversal）：
1. 访问根节点。
2. 递归地对左子树进行先序遍历。
3. 递归地对右子树进行先序遍历。

先序遍历的顺序是先访问根节点，然后按照从左到右的顺序依次访问左子树和右子树。

中序遍历（Inorder traversal）：
1. 递归地对左子树进行中序遍历。
2. 访问根节点。
3. 递归地对右子树进行中序遍历。

中序遍历的顺序是先按照从左到右的顺序递归访问左子树，然后访问根节点，最后按照从左到右的顺序递归访问右子树。

这两种遍历方法都是通过递归实现的，可以用来遍历二叉树或其他类型的树结构。它们在不同的情况下有各自的应用，具体取决于问题的需求。

4.5 示例代码

下面一个简单的示例代码，展示了如何使用Binary Tree和Binary Search Tree进行基本操作：

// 定义二叉树节点类
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

// 二叉树类
class BinaryTree {
    TreeNode root;

    public BinaryTree() {
        root = null;
    }

    // 插入节点
    public void insert(int val) {
        root = insertNode(root, val);
    }

    private TreeNode insertNode(TreeNode node, int val) {
        if (node == null) {
            return new TreeNode(val);
        }

        // 如果值小于当前节点，则插入左子树
        if (val < node.val) {
            node.left = insertNode(node.left, val);
        }
        // 如果值大于等于当前节点，则插入右子树
        else {
            node.right = insertNode(node.right, val);
        }

        return node;
    }

    // 先序遍历
    public void preOrderTraversal() {
        preOrder(root);
    }

    private void preOrder(TreeNode node) {
        if (node == null) {
            return;
        }

        System.out.print(node.val + " ");
        preOrder(node.left);
        preOrder(node.right);
    }
}

// 二叉搜索树类
class BinarySearchTree {
    TreeNode root;

    public BinarySearchTree() {
        root = null;
    }

    // 插入节点
    public void insert(int val) {
        root = insertNode(root, val);
    }

    private TreeNode insertNode(TreeNode node, int val) {
        if (node == null) {
            return new TreeNode(val);
        }

        // 如果值小于当前节点，则插入左子树
        if (val < node.val) {
            node.left = insertNode(node.left, val);
        }
        // 如果值大于等于当前节点，则插入右子树
        else {
            node.right = insertNode(node.right, val);
        }

        return node;
    }

    // 中序遍历
    public void inOrderTraversal() {
        inOrder(root);
    }

    private void inOrder(TreeNode node) {
        if (node == null) {
            return;
        }

        inOrder(node.left);
        System.out.print(node.val + " ");
        inOrder(node.right);
    }
}

// 测试代码
public class myClass {
    public static void main(String[] args) {
        // 创建二叉树，并插入节点
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.insert(5);
        binaryTree.insert(3);
        binaryTree.insert(7);
        binaryTree.insert(2);
        binaryTree.insert(4);
        binaryTree.insert(6);
        binaryTree.insert(8);

        // 先序遍历二叉树
        System.out.print("二叉树 -先序遍历: ");
        binaryTree.preOrderTraversal();
        System.out.println();

        // 创建二叉搜索树，并插入节点
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        binarySearchTree.insert(5);
        binarySearchTree.insert(3);
        binarySearchTree.insert(7);
        binarySearchTree.insert(2);
        binarySearchTree.insert(4);
        binarySearchTree.insert(6);
        binarySearchTree.insert(8);

        // 中序遍历二叉搜索树
        System.out.print("二叉搜索树 - 中序遍历: ");
        binarySearchTree.inOrderTraversal();
        System.out.println();
    }
}

运行结果：

二叉树 -先序遍历: 5 3 2 4 7 6 8 
二叉搜索树 - 中序遍历: 2 3 4 5 6 7 8

五.图（Graph）：

图（Graph）是由节点（Vertex）和边（Edge）组成的一种非线性数据结构，用于表示对象之间的关联关系。可以将节点视为图中的元素，并且节点可以与其他节点通过边相连接。

在实际应用中，图可用于解决各种问题，如社交网络分析、路径搜索、最短路径算法等。在 Java 中，可以自行实现图的数据结构和相关算法，或使用第三方库（如JGraphT、Java Universal Network/Graph Framework等）来操作和处理图结构。

5.1 有向图（Directed Graph）：

也称为有向图、定向图或有向网络。有向图中的边具有方向性，表示节点之间的单向关系。如果节点 A 到节点 B 之间存在一条有向边，那么从节点 A 出发可以到达节点 B，但反过来不行。

5.2 无向图（Undirected Graph）：

也称为无向图、非定向图或无向网络。无向图中的边没有方向，表示节点之间的双向关系。如果节点 A 和节点 B 之间有一条边相连，则可以从节点 A 到节点 B 或者从节点 B 到节点 A。

5.3 使用选择

以下是一些关于使用有向图和无向图的常见场景的选择建议：

使用有向图（Directed Graph）的场景：

城市交通网络：可以将城市视为节点，道路视为有向边，用于表示城市之间的单向道路。
任务依赖关系：可以将任务视为节点，依赖关系视为有向边，用于表示任务之间的执行顺序。
网页链接图：可以将网页视为节点，链接关系视为有向边，用于表示网页之间的跳转链接。

使用无向图（Undirected Graph）的场景：

社交网络分析：可以将人员视为节点，社交关系视为无向边，用于表示人与人之间的双向社交关系。
交通网络规划：可以将地点视为节点，道路视为无向边，用于表示地点之间的双向交通关系。
好友推荐系统：可以将用户视为节点，共同兴趣或交互行为视为无向边，用于推荐潜在好友。

在选择数据结构时，还需考虑算法的时间复杂度和空间复杂度，并根据具体情况做出合适的权衡。

5.4 示例代码

下面是将有向图（Directed Graph）和无向图（Undirected Graph）结合在一起的代码示例：

import java.util.*;

// 有向图类
class DirectedGraph {
    private int V; // 图中节点的数量
    private List<List<Integer>> adjList; // 邻接表表示法

    public DirectedGraph(int nodes) {
        V = nodes;
        adjList = new ArrayList<>(V);

        for (int i = 0; i < V; i++) {
            adjList.add(new ArrayList<>());
        }
    }

    // 添加有向边
    public void addDirectedEdge(int src, int dest) {
        adjList.get(src).add(dest);
    }

    // 获取指定节点的邻居节点列表
    public List<Integer> getOutgoingNeighbors(int node) {
        return adjList.get(node);
    }
}

// 无向图类
class UndirectedGraph {
    private int V; // 图中节点的数量
    private List<List<Integer>> adjList; // 邻接表表示法

    public UndirectedGraph(int nodes) {
        V = nodes;
        adjList = new ArrayList<>(V);

        for (int i = 0; i < V; i++) {
            adjList.add(new ArrayList<>());
        }
    }

    // 添加无向边（边是双向的）
    public void addUndirectedEdge(int src, int dest) {
        adjList.get(src).add(dest);
        adjList.get(dest).add(src);
    }

    // 获取指定节点的邻居节点列表
    public List<Integer> getNeighbors(int node) {
        return adjList.get(node);
    }
}

// 使用示例
public class myClass {
    public static void main(String[] args) {
        int numNodes = 5;

        // 创建有向图对象
        DirectedGraph directedGraph = new DirectedGraph(numNodes);
        directedGraph.addDirectedEdge(0, 1);
        directedGraph.addDirectedEdge(1, 2);
        directedGraph.addDirectedEdge(1, 3);
        directedGraph.addDirectedEdge(2, 4);

        // 创建无向图对象
        UndirectedGraph undirectedGraph = new UndirectedGraph(numNodes);
        undirectedGraph.addUndirectedEdge(0, 1);
        undirectedGraph.addUndirectedEdge(1, 2);
        undirectedGraph.addUndirectedEdge(1, 3);
        undirectedGraph.addUndirectedEdge(2, 4);

        // 获取有向图的节点的出边邻居列表
        System.out.println("有向图的节点 1 的出边邻居列表：" + directedGraph.getOutgoingNeighbors(1));

        // 获取无向图的节点的邻居列表
        System.out.println("无向图的节点 1 的邻居列表：" + undirectedGraph.getNeighbors(1));
    }
}

运行结果：

有向图的节点 1 的出边邻居列表：[2, 3]
无向图的节点 1 的邻居列表：[0, 2, 3]

六.堆（Heap）：

堆是一种特殊的树形数据结构，满足堆属性。堆可以被实现为最大堆或最小堆，用于有效地找到最大值或最小值的数据结构。通过维护最大堆或最小堆的特性，我们可以很方便地实现对数据集合中的最大值或最小值的获取操作，这在某些问题中非常有用，比如Java 提供了优先级队列(PriorityQueue)、排序算法等来实现堆。

6.1 最大堆（Max Heap）：

树的根节点的值就是整个堆中的最大值。也就是说，无论通过什么方式访问堆的元素，我们都能够以O(1)的时间复杂度获取到最大值。此外，最大堆的性质还保证了除了根节点之外的其他节点满足父节点值大于等于子节点值的条件。

6.2 最小堆（Min Heap）：

树的根节点的值就是整个堆中的最小值。同样地，无论如何访问堆的元素，我们都可以以O(1)的时间复杂度获取到最小值。最小堆的性质保证了除了根节点之外的其他节点满足父节点值小于等于子节点值的条件。

6.3 示例代码

下面是一个将最小堆和最大堆的实现结合在一起示例代码，这个示例使用优先级队列（PriorityQueue）类来演示。

import java.util.PriorityQueue;

public class myClass {
    public static void main(String[] args) {
        // 创建最小堆
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        // 添加元素到最小堆
        minHeap.offer(5);
        minHeap.offer(3);
        minHeap.offer(8);
        minHeap.offer(1);

        // 打印最小堆中的最小值（根节点）
        System.out.println("最小值: " + minHeap.peek());

        // 删除最小堆中的最小值
        minHeap.poll();

        // 打印最小堆中的新最小值
        System.out.println("新的最小值: " + minHeap.peek());

        // 创建最大堆
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);

        // 添加元素到最大堆
        maxHeap.offer(5);
        maxHeap.offer(3);
        maxHeap.offer(8);
        maxHeap.offer(1);

        // 打印最大堆中的最大值（根节点）
        System.out.println("最大值: " + maxHeap.peek());

        // 删除最大堆中的最大值
        maxHeap.poll();

        // 打印最大堆中的新最大值
        System.out.println("新的最大值: " + maxHeap.peek());
    }
}

运行结果：

最小值: 1
新的最小值: 3
最大值: 8
新的最大值: 5

七.链表（LinkedList）：

链表是一种线性数据结构，也叫动态数据结构，但是并不会按线性的顺序存储数据，可以根据需要灵活地添加、删除节点，而数组长度固定且连续。

链表（LinkedList）由节点和指针组成，每个节点包含一个数据元素和一个指向下一个节点的指针（单向链表）或同时包含一个指向前一个节点的指针（双向链表）。

链表相比于数组的优势是插入和删除的操作效率高，因为只需要调整相关节点的指针；缺点是访问任意位置的节点时效率较低，需要从头节点开始逐个遍历。

7.1 单向链表：

单向链表中的每个节点包含两个值：当前节点的值和一个指向下一个节点的链接。通过这个链接，我们可以按顺序访问链表中的所有节点。链表的头节点是第一个节点，而尾节点的链接为空。

Java进阶篇--数据结构,Java进阶篇,数据结构,java,算法

7.2 双向链表：

双向链表中的每个节点有三个部分：数值、向后的节点链接和向前的节点链接。与单向链表不同的是，双向链表中的每个节点既可以从前往后遍历，也可以从后往前遍历。双向链表还具有头节点和尾节点，它们分别存储链表的第一个节点和最后一个节点。

Java进阶篇--数据结构,Java进阶篇,数据结构,java,算法

7.3 使用选择

使用单向链表时，通常在以下情况下可以考虑：

插入和删除操作频繁：由于单向链表只需要调整相邻节点的指针，插入和删除操作的效率比较高。
需要按顺序访问数据：单向链表可以按照节点的顺序依次访问，适用于需要按顺序遍历数据的场景。
内存空间有限：单向链表的节点只需要额外存储一个指针，相比于双向链表占用的内存空间更小。

使用双向链表时，通常在以下情况下可以考虑：

需要双向遍历数据：双向链表中的每个节点都包含向前和向后两个指针，可以方便地从头到尾或从尾到头遍历数据。
针对某个节点进行插入和删除操作：由于双向链表具有向前和向后的指针，可以更方便地找到目标节点并进行插入、删除等操作。
对称性要求：如果问题或算法需要对称性操作，双向链表更符合需求。例如，在LRU缓存算法中，为了快速删除最近未使用的节点，经常需要删除和添加节点，而双向链表可以提供更高的效率。

7.4 常用方法

单向链表（Singly Linked List）的常用方法：

insertAtHead(value): 在链表头部插入一个新节点。
insertAtTail(value): 在链表尾部插入一个新节点。
insertAtIndex(index, value): 在指定索引位置插入一个新节点。
deleteAtHead(): 删除链表头部的节点。
deleteAtTail(): 删除链表尾部的节点。
deleteAtIndex(index): 删除指定索引位置的节点。
search(value): 搜索链表中是否存在某个值，并返回对应节点。
getAtIndex(index): 获取指定索引位置的节点值。
isEmpty(): 判断链表是否为空。
size(): 返回链表的长度。
printList(): 打印链表中的所有节点值。

双向链表（Doubly Linked List）的常用方法：

insertAtHead(value): 在链表头部插入一个新节点。
insertAtTail(value): 在链表尾部插入一个新节点。
insertBeforeNode(node, value): 在指定节点之前插入一个新节点。
insertAfterNode(node, value): 在指定节点之后插入一个新节点。
deleteAtHead(): 删除链表头部的节点。
deleteAtTail(): 删除链表尾部的节点。
deleteNode(node): 删除指定节点。
search(value): 搜索链表中是否存在某个值，并返回对应节点。
getAtIndex(index): 获取指定索引位置的节点值。
isEmpty(): 判断链表是否为空。
size(): 返回链表的长度。
printList(): 打印链表中的所有节点值。

7.5 示例代码

// 单向链表节点
class ListNode {
    int val;         // 当前节点的值
    ListNode next;   // 指向下一个节点的指针

    // 构造函数
    public ListNode(int val) {
        this.val = val;
        this.next = null;
    }
}

// 双向链表节点
class DoubleListNode {
    int val;               // 当前节点的值
    DoubleListNode prev;   // 指向前一个节点的指针
    DoubleListNode next;   // 指向下一个节点的指针

    // 构造函数
    public DoubleListNode(int val) {
        this.val = val;
        this.prev = null;
        this.next = null;
    }
}

// 单向链表
class LinkedList {
    private ListNode head;   // 链表头节点

    // 构造函数
    public LinkedList() {
        this.head = null;
    }

    // 在链表末尾添加节点
    public void addNode(int val) {
        ListNode newNode = new ListNode(val);

        if (head == null) {  // 如果链表为空，则新节点为头节点
            head = newNode;
        } else {
            ListNode curr = head;
            while (curr.next != null) {  // 找到链表的最后一个节点
                curr = curr.next;
            }
            curr.next = newNode;  // 将新节点连接到链表末尾
        }
    }

    // 打印链表的所有节点值
    public void printList() {
        ListNode curr = head;
        while (curr != null) {
            System.out.print(curr.val + " ");
            curr = curr.next;
        }
        System.out.println();
    }
}

// 双向链表
class DoublyLinkedList {
    private DoubleListNode head;   // 链表头节点

    // 构造函数
    public DoublyLinkedList() {
        this.head = null;
    }

    // 在链表末尾添加节点
    public void addNode(int val) {
        DoubleListNode newNode = new DoubleListNode(val);

        if (head == null) {  // 如果链表为空，则新节点为头节点
            head = newNode;
        } else {
            DoubleListNode curr = head;
            while (curr.next != null) {  // 找到链表的最后一个节点
                curr = curr.next;
            }
            curr.next = newNode;  // 将新节点连接到链表末尾
            newNode.prev = curr;  // 更新新节点的前驱指针
        }
    }

    // 打印链表的所有节点值
    public void printList() {
        DoubleListNode curr = head;
        while (curr != null) {
            System.out.print(curr.val + " ");
            curr = curr.next;
        }
        System.out.println();
    }
}

// 测试单向链表和双向链表
public class Main {
    public static void main(String[] args) {
        LinkedList linkedList = new LinkedList();
        linkedList.addNode(1);
        linkedList.addNode(2);
        linkedList.addNode(3);
        System.out.print("单向链表: ");
        linkedList.printList();

        DoublyLinkedList doublyLinkedList = new DoublyLinkedList();
        doublyLinkedList.addNode(4);
        doublyLinkedList.addNode(5);
        doublyLinkedList.addNode(6);
        System.out.print("双向链表: ");
        doublyLinkedList.printList();
    }
}

输出结果：

单向链表: 1 2 3 
双向链表: 4 5 6

八.MAP：

当我们需要存储和操作键值对数据时，可以使用Map这个接口。它提供了一种将键映射到值的方法，允许我们通过给定的键快速查找对应的值，类似于字典或者索引。

在Map中，每个键都是唯一的，也就是说不会出现重复的键，而且每个键最多只能映射到一个值。这意味着我们可以依据特定的键来获取对应的值，而不必遍历整个Map。

8.1 常见的Map实现类：

HashMap：HashMap基于哈希表实现，它提供了快速的插入、查找和删除操作。它没有固定的顺序，即插入元素的顺序不会被保留。
TreeMap：TreeMap基于红黑树实现，它会对键进行排序。这使得TreeMap在查找操作上稍慢一些，但它可以按照键的顺序进行遍历。
LinkedHashMap：LinkedHashMap在HashMap的基础上，使用双向链表维护了插入元素的顺序，从而使得遍历顺序和插入顺序相同。它既拥有快速的查找操作，又能保留插入的顺序。

使用Map可以方便地进行数据的检索、插入、删除和更新操作。我们可以通过键来获取对应的值，可以使用put()方法插入键值对，使用remove()方法删除指定的键值对，也可以使用replace()方法更新键对应的值。

8.2 常用的方法

Map接口是Java集合框架中的一部分，用于存储和操作键值对数据。以下是Map接口中常用的方法：

put(key, value)：将指定的键值对存储到Map中，如果键已经存在，则会用新的值替换原有的值。
get(key)：根据指定的键获取对应的值。
remove(key)：根据指定的键从Map中移除对应的键值对。
containsKey(key)：判断Map中是否包含指定的键。
containsValue(value)：判断Map中是否包含指定的值。
isEmpty()：检查Map是否为空，即不包含任何键值对。
size()：返回Map中键值对的数量。
keySet()：返回一个包含所有键的Set集合。
values()：返回一个包含所有值的Collection集合。
entrySet()：返回一个包含所有键值对（Entry对象）的Set集合。

以上是Map接口中常见的方法。实际使用时，可以根据需要选择适当的方法来进行键值对的存储、获取、删除和判断操作。同时，需要注意的是，Map中的键是唯一的，因此在使用put()方法添加键值对时，要确保键的唯一性。

8.3 使用选择

Map适用于许多场景，特别是当我们需要根据键进行快速查找时。比如，在存储学生信息时，我们可以把学生的学号作为键，将学生对象作为值，这样就可以根据学号快速找到对应的学生信息。另外，Map还可以用于统计词频、缓存数据等方面。

总而言之，Map提供了一种灵活且高效的存储和查找键值对数据的方式，能够满足各种不同场景的需求。

8.4 示例代码

下面是一些使用Map接口方法的示例代码：

import java.util.Collection;
import java.util.HashMap;
import java.util.Map;
import java.util.Set;

public class Main{
    public static void main(String[] args) {
        // 创建一个HashMap对象作为Map实现类
        Map<String, Integer> map = new HashMap<>();

        // 向Map中添加键值对
        map.put("apple", 10);
        map.put("banana", 5);
        map.put("orange", 8);

        // 获取键对应的值
        int appleQuantity = map.get("apple");
        System.out.println("苹果数量：" + appleQuantity);

        // 判断Map是否包含指定的键或值
        boolean containsBanana = map.containsKey("banana");
        boolean containsValue8 = map.containsValue(8);
        System.out.println("是否包含香蕉：" + containsBanana);
        System.out.println("是否包含值为8的键值对：" + containsValue8);

        // 移除指定的键值对
        map.remove("orange");

        // 遍历Map中的键值对
        for (Map.Entry<String, Integer> entry : map.entrySet()) {
            String key = entry.getKey();
            int value = entry.getValue();
            System.out.println("水果：" + key + "，数量：" + value);
        }

        // 获取Map中键的集合
        Set<String> keySet = map.keySet();
        System.out.println("所有水果的名称：" + keySet);

        // 获取Map中值的集合
        Collection<Integer> values = map.values();
        System.out.println("所有水果的数量：" + values);
    }
}

输出结果：文章来源地址https://www.toymoban.com/news/detail-659829.html

苹果数量：10
是否包含香蕉：true
是否包含值为8的键值对：true
水果：banana，数量：5
水果：apple，数量：10
所有水果的名称：[banana, apple]
所有水果的数量：[5, 10]

到了这里，关于Java进阶篇--数据结构的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

Java进阶篇--数据结构

一.数组（Array）：

1.1 特点：

1.2 基本操作：

1.3 使用数组的好处包括：

1.4 数组也有一些限制：

二.集合框架（Collections Framework）：

2.1 列表（List）：

2.1.1 数组列表（ArrayList）：

扩展知识：

方法：

ArrayList的遍历方式

ArrayList<E>使用泛型

Arrays工具类

2.1.2 链表（LinkedList）：

常用方法：

2.1.3 使用选择：

2.1.4 示例代码：

2.2 集（Set）：

2.2.1 哈希集（HashSet）：

基本类型对应的包装类表如下：

HashSet的常用方法包括：

2.2.2 树集（TreeSet）：

TreeSet的常用方法包括：

2.2.3 使用选择：

2.2.4 示例代码：

2.3 映射（Map）：

2.3.1 哈希映射（HashMap）：

2.3.2 树映射（TreeMap）：

2.3.3 使用选择

2.3.4 示例代码

三.栈（Stack）和队列（Queue）：

3.1方法

3.2示例代码

四.树（Tree）：

4.1 二叉树（Binary Tree）：

4.2二叉搜索树（Binary Search Tree）：

4.3 操作方法

4.4 树的遍历

4.4.1树的遍历包括两种主要方式：

4.4.2 树的两种基本遍历方式：

4.5 示例代码

五.图（Graph）：

5.1 有向图（Directed Graph）：

5.2 无向图（Undirected Graph）：

5.3 使用选择

5.4 示例代码

六.堆（Heap）：

6.1 最大堆（Max Heap）：

6.2 最小堆（Min Heap）：

6.3 示例代码

七.链表（LinkedList）：

7.1 单向链表：

7.2 双向链表：

7.3 使用选择

7.4 常用方法

7.5 示例代码

八.MAP：

8.1 常见的Map实现类：

8.2 常用的方法

8.3 使用选择

8.4 示例代码

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2