数学建模之“TOPSIS数学模型”原理和代码详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模之“TOPSIS数学模型”原理和代码详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、简介

TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）是一种多准则决策分析方法，用于解决多个候选方案之间的排序和选择问题。它基于一种数学模型，通过比较每个候选方案与理想解和负理想解之间的相似性来评估其优劣。

TOPSIS方法包括以下步骤：

确定决策准则：首先确定影响决策的准则，例如成本、效益、可行性等。这些准则应该能够量化，并与候选方案相关联。
归一化：对每个准则进行归一化处理，将其转化为标准化的0-1范围内的值。这样可以确保不同准则的权重在计算中得到平等的考虑。
确定理想解和负理想解：根据每个准则的重要性，确定一个理想解和一个负理想解。理想解是在各个准则上表现最佳的方案，而负理想解则是在各个准则上表现最差的方案。
计算相似性：使用距离度量方法（如欧几里得距离或曼哈顿距离）计算每个候选方案与理想解和负理想解之间的相似性。
计算综合评分：根据相似性计算每个候选方案的综合评分。综合评分越接近1，表示该方案越接近理想解；综合评分越接近0，表示该方案越接近负理想解。
排序和选择：按照综合评分对候选方案进行排序，并选择得分最高的方案作为最优解。

TOPSIS方法的优点包括简单易用、不需要主观权重设定、能够有效处理多准则决策问题。然而，它也有一些限制，例如对准则之间的相互关系没有考虑，不能处理不确定性和不完备信息等。

总之，TOPSIS数学模型是一种常用的多准则决策方法，可以帮助决策者在多个候选方案中做出合理的选择和排序。

二、实例

以下是一个典型的TOPSIS例题：

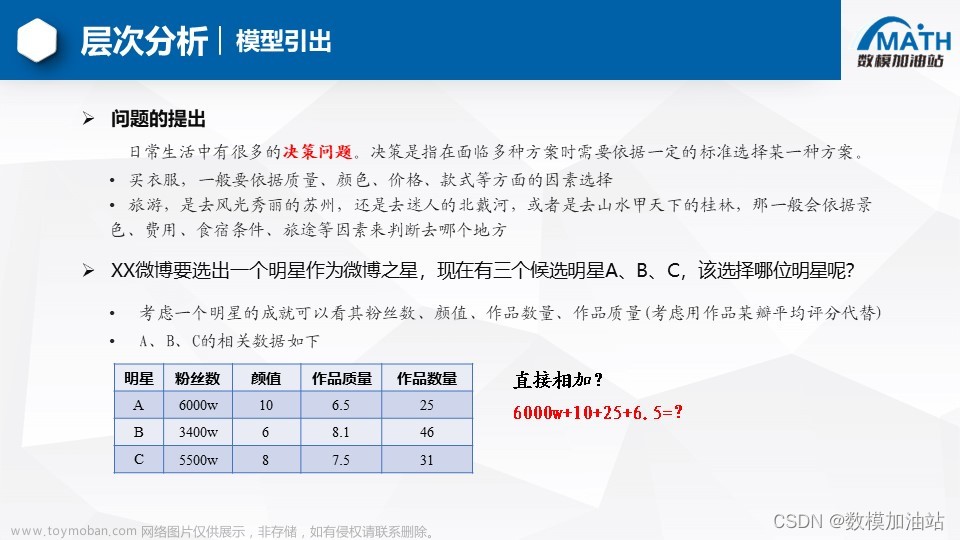
假设你是一家公司的采购经理，你需要从三个供应商中选择一个最佳的供应商来购买某种原材料。你考虑的准则有：价格、质量和交货时间。根据这些准则，你收集到了每个供应商的数据如下：

供应商A：价格 8, 质量 9, 交货时间 5
供应商B：价格 6, 质量 7, 交货时间 8
供应商C：价格 9, 质量 8, 交货时间 7

现在使用TOPSIS方法来选择最佳供应商。

1. 归一化：
首先，对每个准则进行归一化处理，将它们转化为0-1范围内的标准化值。这里我们可以使用最小-最大归一化方法。

供应商A：价格 8/9 ≈ 0.89, 质量 9/9 = 1, 交货时间 5/9 ≈ 0.56
供应商B：价格 6/9 ≈ 0.67, 质量 7/9 ≈ 0.78, 交货时间 8/9 ≈ 0.89
供应商C：价格 9/9 = 1, 质量 8/9 ≈ 0.89, 交货时间 7/9 ≈ 0.78

2. 确定理想解和负理想解：
根据每个准则的重要性，确定理想解和负理想解。对于价格和交货时间，理想解是最小值，负理想解是最大值；对于质量，理想解是最大值，负理想解是最小值。

理想解：价格 0, 质量 1, 交货时间 0
负理想解：价格 1, 质量 0, 交货时间 1

3. 计算相似性：
使用距离度量方法（如欧几里得距离）计算每个供应商与理想解和负理想解之间的相似性。

供应商A：与理想解的相似性 = √((0.89-0)^2 + (1-0)^2 + (0.56-0)^2) ≈ 1.12
与负理想解的相似性 = √((0.89-1)^2 + (1-0)^2 + (0.56-1)^2) ≈ 0.84
供应商B：与理想解的相似性 = √((0.67-0)^2 + (0.78-1)^2 + (0.89-0)^2) ≈ 0.73
与负理想解的相似性 = √((0.67-1)^2 + (0.78-0)^2 + (0.89-1)^2) ≈ 1.24
供应商C：与理想解的相似性 = √((1-0)^2 + (0.89-1)^2 + (0.78-0)^2) ≈ 0.26
与负理想解的相似性 = √((1-1)^2 + (0.89-0)^2 + (0.78-1)^2) ≈ 1.12

4. 计算综合评分：
根据相似性计算每个供应商的综合评分，使用正负理想解的相对距离。

供应商A：综合评分 = 0.84 / (0.84 + 1.12) ≈ 0.43
供应商B：综合评分 = 1.24 / (0.73 + 1.24) ≈ 0.63
供应商C：综合评分 = 0.26 / (0.26 + 1.12) ≈ 0.19

5. 排序和选择：
根据综合评分对供应商进行排序，并选择得分最高的供应商作为最优解。

综合评分排序：供应商B > 供应商A > 供应商C

因此，在这个例子中，供应商B被认为是最佳供应商，因为它在价格、质量和交货时间准则上相对于其他供应商更接近理想解。