SM2椭圆曲线公钥密码算法实现项目-Toy模板网

这篇具有很好参考价值的文章主要介绍了SM2椭圆曲线公钥密码算法实现项目。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、实验目的

Python 3.9 、PyCharm

二、方案设计

1.背景：

SM2椭圆曲线公钥密码算法是我国自主设计的公钥密码算法，包括SM2-1椭圆曲线数字签名算法，SM2-2椭圆曲线密钥交换协议，SM2-3椭圆曲线公钥加密算法，分别用于实现数字签名密钥协商和数据加密等功能。

2.原理：

（1）有限域上的椭圆曲线上的点的加法

（2）dB*C1=dB*k*G=k*(dB*G)=k*PB，这样保证了密钥在加密过程和解密过程中是一致的。

（3）哈希函数输出杂凑值

（4）Hass定理

3.算法步骤：

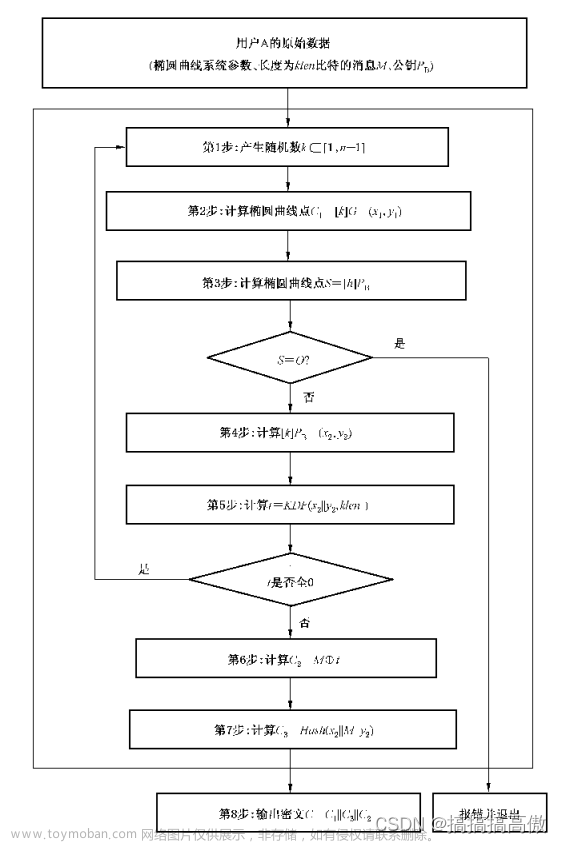
加密过程：

设需要发送的消息为比特串M ，klen为M的比特长度。

为了对明文M进行加密，作为加密者的用户A应实现以下运算步骤：

A1：用随机数发生器产生随机数k∈[1,n-1]；

A2：计算椭圆曲线点 C1=[k]G=(x1,y1)，（[k]G 表示 k*G ）将C1的数据类型转换为比特串；

A3：计算椭圆曲线点 S=[h]PB，若S是无穷远点，则报错并退出；

A4：计算椭圆曲线点 [k]PB=(x2,y2)，将坐标 x2、y2 的数据类型转换为比特串；

A5：计算t=KDF(x2∥y2，klen)，若 t 为全0比特串，则返回 A1；

A6：计算C2 = M⊕t；

A7：计算C3 = Hash(x2∥M∥y2)；

A8：输出密文C = C1∥C2∥C3。

解密过程：

设klen为密文中C2的比特长度。

为了对密文C=C1∥C2∥C3 进行解密，作为解密者的用户B应实现以下运算步骤：

B1：从C中取出比特串C1，将C1的数据类型转换为椭圆曲线上的点，验证C1是否满足椭圆曲线方程，若不满足则报错并退出；

B2：计算椭圆曲线点 S=[h]C1，若S是无穷远点，则报错并退出；

B3：计算[dB]C1=(x2,y2)，将坐标x2、y2的数据类型转换为比特串；

B4：计算t=KDF(x2∥y2，klen)，若t为全0比特串，则报错并退出；

B5：从C中取出比特串C2，计算M′= C2⊕t；

B6：计算u = Hash(x2∥M′∥y2)，从C中取出比特串C3，若u != C3，则报错并退出；

B7：输出明文M′。

三、方案实现

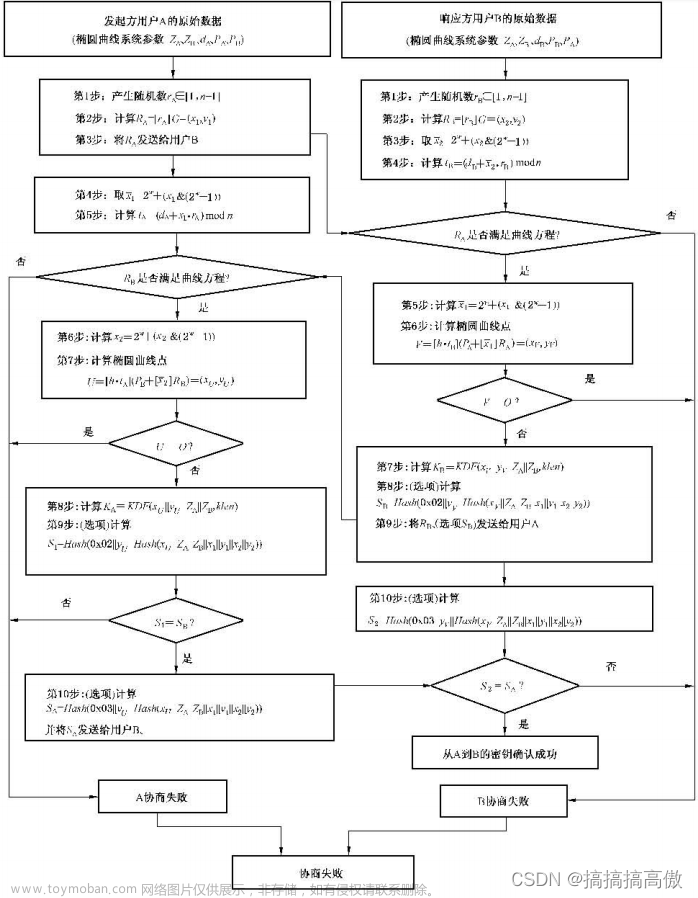
算法流程图：

sm2算法实现,算法,python,开发语言,网络安全

四、实验源码

1.主要函数

addPoint：点加运算

multiPoint：多倍点运算

KDF：产生长度为klen的密钥数据比特串

enCryto：加密函数

deCryto：解密函数

2.代码

import hashlib
import math
import random
import sys

class SM2:

    def getInverse(self,a):
        return pow(a,self.p-2,self.p)

    def addPoint(self,pointA,pointB=None):
        if pointB==None:
            temp=(3*pow(pointA[0],2)+self.a)*self.getInverse((2*pointA[1]))  
            x3=temp**2-2*pointA[0]
            x3%=self.p
            y3=temp*(pointA[0]-x3)-pointA[1]
            y3%=self.p
        elif pointA==[0,0] or pointB==[0,0]:
            x3=pointA[0]+pointB[0]
            y3=pointA[1]+pointB[1]
        else:
            temp=(pointA[1]-pointB[1])*self.getInverse(pointA[0]-pointB[0])
            x3=temp**2-pointA[0]-pointB[0]
            x3%=self.p
            y3=temp*(pointA[0]-x3)-pointA[1]
            y3%=self.p
        return x3,y3

    def multiPoint(self,point,k):
        multiPoint=[0,0]
        doublePoint=point
        while k>0:
            if k%2:
                multiPoint[0],multiPoint[1]=self.addPoint(multiPoint,doublePoint)
            k//=2
            doublePoint=self.addPoint(doublePoint)
        return multiPoint[0],multiPoint[1]


    def hex(self,num):
        num=hex(num).upper()[2:]
        return "0"*(64-len(num))+num

    
    def KDF(self,bitnum,klen):
        Ha=""
        hs=hashlib.sha256()    #产生长度为64的十六进制字符串作为消息摘要
        if klen>(2**32-1)*64:
            print("too long to caculate")
        rct=math.ceil(klen/64)
        for i in range(rct):
            ct=hex(i+1).upper()[2:]
            ct="0"*(32-len(ct))+ct
            x2y2ct=bitnum+ct
            hs.update(x2y2ct.encode("ascii"))
            Ha+=hs.hexdigest()  #返回摘要，作为十六进制数据字符串值
        return Ha[0:klen]
    

    def __init__(self):
        self.p=0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
        self.a=0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
        self.b=0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
        self.n=0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
        self.Gx=0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
        self.Gy=0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
        self.h=1      #Hass定理
        self.setSecretKey(True)
        self.PBx,self.PBy=self.multiPoint([self.Gx,self.Gy],self.d)
        print("公钥:({},{})".format(self.hex(self.PBx),self.hex(self.PBy)))
        if self.PBx+self.PBy==0:
            sys.exit(-1)
        hs=hashlib.sha256()

    def setSecretKey(self,show=False):
        self.d=random.randint(1,self.n)
        if show:
            print("私钥为:",self.hex(self.d))

    def enCryto(self,s:str):
        numt=0
        while numt==0:
            k=random.randint(1,self.n) #A1
            print("加密过程中生成随机数",self.hex(k))
            c1x,c1y=self.multiPoint([self.Gx,self.Gy],k) #A2
            print("C1点的坐标:({},{})".format(self.hex(c1x),self.hex(c1y)))
            C1=self.hex(c1x)+self.hex(c1y)
            print("C1为:",C1)
            x2,y2=self.multiPoint([self.PBx,self.PBy],k)  #A4
            x2y2connet=hex(x2).upper()[2:]+hex(y2).upper()[2:]
            s=s.encode("ascii")
            s=s.hex() 
            klen=len(s)
            t=self.KDF(x2y2connet,klen).upper()  #A5
            print(t)
            numt=int(t,16)
        C2=hex(int(s,16)^int(t,16)).upper()[2:]
        print("C2为:",C2)
        print(x2,s,y2,"?")
        C3=self.hex(x2)+s+self.hex(y2)
        hs=hashlib.sha256()
        hs.update(C3.encode("ascii"))
        C3=hs.hexdigest().upper()
        print("C3为:",C3)
        return C1+C2+C3
    
    def deCryto(self,c1c2c3):
        clen=len(c1c2c3)   #切片
        c1=c1c2c3[0:128]
        c2=c1c2c3[128:clen-64]
        c3=c1c2c3[-64:]
        x1=c1[0:64]
        y1=c1[64:128]
        x1=int(x1,16)
        y1=int(y1,16)
        left=pow(y1,2,self.p)
        right=pow(x1,3,self.p)+self.a*x1+self.b
        right%=self.p
        if left!=right: #C1和S验证
            sys.exit(-1)
        x2,y2=self.multiPoint([x1,y1],self.d)
        print("x2为:",x2)
        print("y2为:",y2)
        x2y2connet=hex(x2).upper()[2:]+hex(y2).upper()[2:]
        t=self.KDF(x2y2connet,len(c2))
        if int(t,16)==0:
            sys.exit(-1)
        Mm=hex(int(c2,16)^int(t,16)).upper()[2:]
        print("M`为:",Mm)
        u=self.hex(x2)+Mm+self.hex(y2)
        hs=hashlib.sha256()
        hs.update(u.encode("ascii"))
        print("x2||M||y2的哈希为:",hs.hexdigest().upper())
        if hs.hexdigest().upper()!=c3:
            sys.exit(-1)
        return bytes.fromhex(Mm)

def main():
    plaintxt=input()
    sm2=SM2()
    secret=sm2.enCryto(plaintxt)
    print("密文为:",secret)
    msg=sm2.deCryto(secret)
    print("明文为:",msg.decode("ascii"))

if __name__=="__main__":
    main()