第一部分:Ed25519算法的简介与重要性
随着数字加密技术的飞速发展,我们不断地探索更安全、更高效的加密算法来保护数据和身份验证。其中,Ed25519已经成为了椭圆曲线数字签名算法(ECDSA)的一个重要分支,其在性能和安全性方面都表现出了卓越的特点。
-
Ed25519的特点:
- 安全性: Ed25519相对于传统的ECDSA有着更好的安全性。
- 效率: 它的运行效率非常高,适合在各种设备上执行,包括移动设备。
- 短签名: 它产生的签名非常短,只有64字节。
-
为什么选择Ed25519?
选择Ed25519的主要原因是它结合了速度、安全性和简单性。它消除了多种可能的实施差异,这意味着它比其他加密方法更不容易受到侧信道攻击。
C#移植的背景与动机
C#作为一种广泛使用的编程语言,尤其在.NET框架中,有大量的应用程序和服务运行在这个框架上。因此,将Ed25519移植到C#可以为.NET开发者提供一个强大、高效和安全的数字签名工具。
具体的移植过程涉及了复杂的数学和编程技巧,下面我们会通过一个简化的示例来展示如何在C#中实现Ed25519算法。
C#实现示例
首先,确保你有.NET的基本知识,以及一些关于椭圆曲线加密的背景知识。
// 前置定义
public const int PublicKeyLength = 32;
public const int PrivateKeyLength = 64;
public const int SignatureLength = 64;
public const int KeySizeInBits = 256;
创建Ed25519的主类,并定义基本的属性和方法:
public class Ed25519
{
private readonly byte[] _privateKey;
private readonly byte[] _publicKey;
public Ed25519(byte[] privateKey, byte[] publicKey)
{
if (privateKey.Length != PrivateKeyLength || publicKey.Length != PublicKeyLength)
{
throw new ArgumentException("Invalid key length");
}
_privateKey = privateKey;
_publicKey = publicKey;
}
// 这里是签名和验证方法的占位符
}
为了方便理解,我们只展示了部分代码。实际上,这个类还需要包括签名生成和验证等核心功能。
具体过程请下载完整项目。
第二部分:核心签名和验证过程
现在我们将继续深入Ed25519的核心部分,即如何生成数字签名以及如何验证给定的签名是否有效。
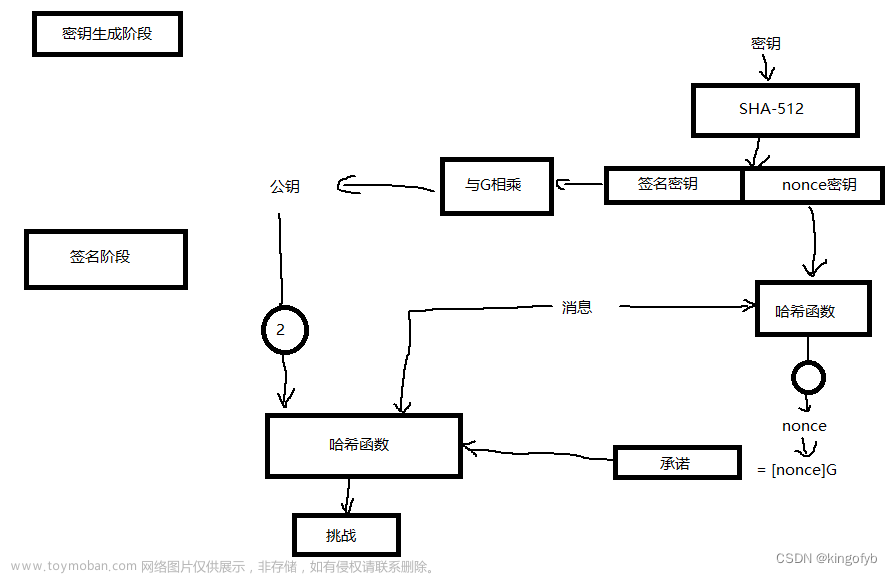
1. 签名生成
要生成Ed25519的签名,我们需要私钥和一个消息。基本步骤如下:
- 使用私钥和消息计算哈希值。
- 使用哈希值和私钥生成签名。
这里是简化版的C#代码:
public byte[] Sign(byte[] message)
{
if (message == null) throw new ArgumentNullException(nameof(message));
// 计算哈希
byte[] hash = ComputeHash(_privateKey, message);
// 生成签名
byte[] signature = GenerateSignature(hash);
return signature;
}
2. 验证签名
要验证Ed25519的签名,我们需要公钥、原始消息和其对应的签名。核心思想是用公钥重新计算一个签名,然后比较它是否与给定的签名匹配。
这里是简化版的C#代码:
public bool Verify(byte[] message, byte[] signature)
{
if (message == null) throw new ArgumentNullException(nameof(message));
if (signature.Length != SignatureLength) throw new ArgumentException("Invalid signature length");
// 使用公钥计算签名
byte[] computedSignature = ComputeSignature(_publicKey, message);
// 比较计算的签名与给定的签名
return AreSignaturesEqual(computedSignature, signature);
}
在这两个核心函数中,我们依赖于一些未显示的辅助函数,如ComputeHash、GenerateSignature和AreSignaturesEqual。这些函数执行加密哈希计算、真正的签名生成以及签名比较。
应用场景
由于Ed25519提供了高性能和安全的数字签名,因此它在多种场景中都非常有用:
- 身份验证: 服务器和客户端之间的通信常常需要双方身份的互相验证,确保消息的来源可靠。
- 数据完整性: 验证数据是否在传输过程中被修改。
- 合同数字化: 在数字化合同中使用Ed25519可以确保合同的内容未被更改,并且签名者的身份得到验证。
下面我们将探讨Ed25519与其他加密算法的比较,以及它在现实世界中的使用案例。
第三部分:Ed25519与其他加密算法的比较及现实应用案例
1. Ed25519与其他加密算法的比较
椭圆曲线加密技术已经存在了很长时间,并被应用在许多加密方案中。然而,不是所有的椭圆曲线加密都相同,Ed25519与其他常见算法的主要区别如下:
- 性能: 由于Ed25519的特殊设计,它在大多数情况下比传统的ECDSA算法更快。
- 签名大小: Ed25519的签名大小为64字节,比很多其他算法的签名更短,这使得它在网络传输和存储方面更为高效。
- 安全性: Ed25519的设计目标之一就是提供强大的安全性,同时减少可能的实现差异和侧信道攻击。
2. 现实应用案例
Ed25519因其高效和安全而在多个现实世界的应用中受到欢迎:
- 分布式版本控制系统: 如Git,使用Ed25519进行签名验证,以确保代码的完整性和来源。
- 安全通讯: 诸如Signal和WhatsApp这样的通讯应用使用Ed25519来验证消息的完整性和发送者的身份。
- 区块链: 许多现代的区块链技术,如Stellar和Solana, 使用Ed25519作为其核心的签名算法,由于其高效和安全性,使得大量交易能够迅速和安全地处理。
结论与未来发展
Ed25519已经成为当今最受欢迎和最受信任的数字签名算法之一。其在C#上的移植使得.NET开发者能够更方便地在他们的应用和服务中应用这一先进的技术。
尽管Ed25519在当前的应用中表现得很好,但随着技术的发展和新的攻击手段的出现,我们总是需要持续地评估和更新我们使用的安全技术。为此,持续的研究和开发是必不可少的,以确保我们的数据和通信始终受到最佳的保护。
为了深入探讨该技术或参考完整的C#移植实现,我们强烈建议下载和查看完整项目。这将为你提供一个完整的框架和理解,使你能够在自己的.NET项目中有效地利用Ed25519。文章来源:https://www.toymoban.com/news/detail-660608.html
感谢你的耐心阅读,希望这篇文章能够帮助你深入理解Ed25519和其在.NET环境中的应用。如果你有任何问题或反馈,请随时与我们联系。文章来源地址https://www.toymoban.com/news/detail-660608.html
到了这里,关于深入解析Ed25519椭圆曲线数字签名算法的C#移植及应用示例的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!