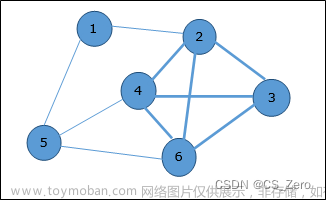
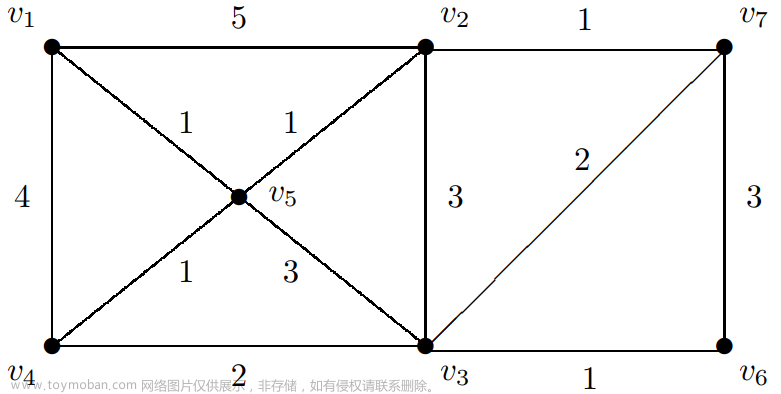
1. 拓扑排序+bitset
题目链接:Acwing164 可达性统计
第一次使用bitset,复杂度:N/32,比N小
所以总的时间复杂度为O(N*(N+M)/32)
#include <iostream>
#include <bitset>
#include <queue>
using namespace std;
const int N = 3e4+20;
bitset<N> f[N];
struct NODE{
int to, next;
}edge[N];
int head[N], cnt, inv[N], n, m;
void add(int u, int v) {
++cnt;
edge[cnt].to = v, edge[cnt].next = head[u], head[u] = cnt;
}
void topo() {
queue<int> q;
for(int i=1; i<=n; i++) {
if(!inv[i]) q.push(i);
}
while(!q.empty()) {
int x = q.front();
q.pop();
f[x][x] = 1; //自己可到达
for(int i = head[x]; i; i = edge[i].next) {
int v = edge[i].to;
f[v] |= f[x];
inv[v]--;
if(!inv[v]) q.push(v);
}
}
for(int i=1; i<=n; i++) printf("%d\n", f[i].count()); //二进制中1的个数
}
int main() {
int u, v; scanf("%d%d", &n, &m);
while(m--){
scanf("%d%d", &u, &v);
add(v, u); //反向建图
inv[u]++;
}
topo();
return 0;
}
2. 01分数规划, spfa判断正环
题目链接:Acwing 观光奶牛

#include <bits/stdc++.h>
using namespace std;
const int N = 1050, M = 5005;
int head[N], cnt, n, ct[N], st[N];
double dis[N], f[N];
struct NODE{
int to, next, w;
}edge[M];
void add(int u, int v, int w){
++cnt;
edge[cnt].to = v, edge[cnt].next = head[u], head[u] = cnt;
edge[cnt].w = w;
}
bool spfa(double mid) {
queue<int> q;
for(int i=1; i<=n; i++) q.push(i), st[i] = true, dis[i] = ct[i] = 0;
while(!q.empty()) {
int x = q.front();
q.pop();
st[x] = false;
for(int i = head[x]; i; i = edge[i].next) {
int v = edge[i].to;
if( dis[v] < dis[x] + f[x] - mid * edge[i].w) { //判断正环
dis[v] = dis[x] + f[x] - mid * edge[i].w;
ct[v] = ct[x]+1;
if(ct[v] >= n) return true;
if(!st[v]) {
q.push(v), st[v] = true;
}
}
}
}
return false;
}
int main() {
int p; scanf("%d%d", &n, &p);
for(int i=1; i<=n; i++) cin >> f[i];
int a, b, w;
while(p--) {
scanf("%d%d%d", &a, &b, &w);
add(a, b, w);
}
double l = 0, r = 1010, eps = 1e-4;
while(r-l > eps) {
double mid = (l+r)/2;
if(spfa(mid)) l = mid;
else r =mid;
}
printf("%.2lf", l);
return 0;
}3. dp, 统计s点到t点的最短路/次短路有多少条
题目链接:cf div3. G. Counting Shortcuts文章来源:https://www.toymoban.com/news/detail-661433.html
需要注意dp的转移顺序文章来源地址https://www.toymoban.com/news/detail-661433.html
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5+10, M = 4e5+10, mod = 1e9+7;
int st, ed;
bool walked[N];
int cnt, head[N], depth[N];
vector<int> vec[N];
ll dp[N][2]; //dp[i][0/1]代表从s到i点为最/次短路有多少条路径
struct EDGE{
int to, next;
}edge[M];
void add(int u, int v){
++cnt;
edge[cnt].to = v, edge[cnt].next = head[u], head[u] = cnt;
}
void bfs(){
queue<int> q;
q.push(st);
walked[st] = 1;
depth[st] = 0;
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = head[x]; i; i = edge[i].next){
int v = edge[i].to;
if(walked[v]) continue;
q.push(v);
walked[v] = 1;
depth[v] = depth[x]+1;
}
}
}
int main() {
int T; scanf("%d", &T);
while(T--){
int n, m, u, v; scanf("%d%d", &n, &m);
for(int i = 1; i<=n; i++) head[i] = walked[i] = dp[i][0] = dp[i][1] = 0;
for(int i = 1; i<=cnt; i++) edge[cnt].to = edge[cnt].next = 0;
cnt = 0;
scanf("%d%d", &st, &ed);
while(m--){
scanf("%d%d", &u, &v);
add(u, v), add(v, u);
}
bfs(); //处理出深度
for(int i = 0; i<=depth[ed]; i++) vec[i].clear();
for(int i = 1; i<=n; i++) {
vec[depth[i]].emplace_back(i);
}
dp[st][0]= 1;
for(int i = 0; i <= depth[ed]; i++) { //枚举深度
for(int j = 0; j<vec[i].size(); j++){ //先转移同一层的
int uu = vec[i][j]; //深度为i的点uu
for(int k = head[uu]; k; k = edge[k].next) {
int vv = edge[k].to; //与uu相邻的点vv
if(depth[vv]==i) dp[vv][1] = (dp[vv][1] + dp[uu][0])%mod;
}
}
for(int j = 0; j<vec[i].size(); j++){ //再转移下一层的
int uu = vec[i][j]; //深度为i的点uu
for(int k = head[uu]; k; k = edge[k].next) {
int vv = edge[k].to; //与uu相邻的点vv
if(depth[vv]==i+1) dp[vv][0] = (dp[vv][0] + dp[uu][0])%mod, dp[vv][1] = (dp[vv][1] + dp[uu][1])%mod;
}
}
}
ll ans = (dp[ed][1] + dp[ed][0])%mod;
printf("%lld\n", ans);
}
return 0;
}
//因为该层的dp[0], dp[1]转移给下一层的dp[0], dp[1]
//而该层的dp[0]由上一层转移而来(没有问题),而该层的dp[1]却还可以由同一层的dp[0]转移而来
//因此我们应该先把该层的dp[1]转移完,再把本层的转移给下一层到了这里,关于图论相关问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!