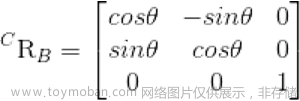最近一直忙于工作,每天都在写一些业务代码。而目前工程中的技术栈并没有使用旋量这一套机器人理论系统,因此时间长了自己都忘记了。
于是决定把这本书配套的代码内容也过一遍,查漏补缺,把这本书的笔记内容完结一下。
代码来源于github:https://github.com/NxRLab/ModernRobotics
其中Python部分,相关的函数一共有47个,其实也不是很多。
读者朋友们可以配合我的专栏地址一起学习:
【现代机器人学】学习笔记
目录
刚体变换部分:
NearZero:判断是否接近0
Normalize:向量归一化
RotInv:旋转矩阵求逆
VecToso3:向量到so3
so3ToVec:so3到向量
AxisAng3:旋转三维矢量到轴角
MatrixExp3:矩阵指数积,so3到旋转矩阵
MatrixLog3:矩阵对数,旋转矩阵到so3
RpToTrans:旋转平移构造齐次矩阵
TransToRp:齐次矩阵拆分旋转平移
TransInv:齐次矩阵的逆矩阵
VecTose3:向量到se3
se3ToVec:se3到向量
Adjoint:计算齐次矩阵的伴随矩阵
ScrewToAxis:螺旋轴qsh到标准螺旋轴:
AxisAng6:旋量到螺旋轴的正则化过程
MatrixExp6:se3到齐次矩阵
MatrixLog6:齐次矩阵到se3
ProjectToSO3:找到和SO3最近的矩阵
ProjectToSE3:找到和SE3最接近的矩阵
DistanceToSO3:计算距离SO3的距离
DistanceToSE3:计算距离SE3的距离
TestIfSO3:检查输入矩阵是否是SO3
TestIfSE3:检查输入矩阵是否是SE3
机器人运动学部分:
FKinBody:基于Body系进行FK计算
FKinSpace:基于Space系进行FK计算
JacobianSpace:基于Space系的机器人雅可比
JacobianBody:基于Body系的机器人雅可比
IKinSpace:基于Space系的机器人逆运动学
IKinBody:基于Body系的机器人逆运动学
机器人动力学部分:
ad: 旋量李括号(叉积伴随运算)
InverseDynamics:逆动力学算法
MassMatrix:计算质量矩阵
VelQuadraticForces:计算科里奥力项和向心项
GravityForces:计算克服重力所需的关节力/力矩
EndEffectorForces:计算创建末端执行器力Ftip所需的关节力/扭矩
ForwardDynamics:前向动力学
逆动力学算法可用于计算(总结一下):
EulerStep:欧拉积分工具函数
InverseDynamicsTrajectory :给定轨迹,计算轨迹中各时刻的关节力矩
ForwardDynamicsTrajectory:给定关节力矩序列,推算机械臂运动
机器人轨迹生成部分:
CubicTimeScaling:三次多项式缩放时间尺度
QuinticTimeScaling:五次多项式缩放时间尺度
如何计算三次/五次多项式的系数?
JointTrajectory:关节空间轨迹平滑插值
ScrewTrajectory:螺旋轴空间平滑插值
CartesianTrajectory:笛卡尔空间平滑插值
机器人控制部分:
ComputedTorque:计算特定时刻的关节控制力矩
SimulateControl:模拟力矩控制器去跟随一条期望的机器人轨迹
下面开始:
刚体变换部分:
NearZero:判断是否接近0
def NearZero(z):
"""Determines whether a scalar is small enough to be treated as zero
:param z: A scalar input to check
:return: True if z is close to zero, false otherwise
Example Input:
z = -1e-7
Output:
True
"""
return abs(z) < 1e-6这个函数是判断输入的标量是否接近于0,比较简单。
当然,如果输入是向量,则会返回一个装有true或false的列表,指明各项是否接近0。
Normalize:向量归一化
def Normalize(V):
"""Normalizes a vector
:param V: A vector
:return: A unit vector pointing in the same direction as z
Example Input:
V = np.array([1, 2, 3])
Output:
np.array([0.26726124, 0.53452248, 0.80178373])
"""
return V / np.linalg.norm(V)这个函数的作用是对向量进行归一化,即方向不变,除以模长。而np.linalg.norm()用于求范数,linalg本意为linear(线性) + algebra(代数),norm则表示范数。默认是2范数,即元素之和开平方。
RotInv:旋转矩阵求逆
def RotInv(R):
"""Inverts a rotation matrix
:param R: A rotation matrix
:return: The inverse of R
Example Input:
R = np.array([[0, 0, 1],
[1, 0, 0],
[0, 1, 0]])
Output:
np.array([[0, 1, 0],
[0, 0, 1],
[1, 0, 0]])
"""
return np.array(R).T求旋转矩阵的逆矩阵。我们知道旋转矩阵的特性是,其逆矩阵与转置矩阵相同。因此求逆速度可以大幅度加快。
VecToso3:向量到so3
def VecToso3(omg):
"""Converts a 3-vector to an so(3) representation
:param omg: A 3-vector
:return: The skew symmetric representation of omg
Example Input:
omg = np.array([1, 2, 3])
Output:
np.array([[ 0, -3, 2],
[ 3, 0, -1],
[-2, 1, 0]])
"""
return np.array([[0, -omg[2], omg[1]],
[omg[2], 0, -omg[0]],
[-omg[1], omg[0], 0]])这个函数对应公式:

即把一个向量转化为so3的矩阵表示。我们知道旋转矩阵的表示则是:

即通过轴角可转化为旋转矩阵。这个之后介绍。
与此相反,
so3ToVec:so3到向量
def so3ToVec(so3mat):
"""Converts an so(3) representation to a 3-vector
:param so3mat: A 3x3 skew-symmetric matrix
:return: The 3-vector corresponding to so3mat
Example Input:
so3mat = np.array([[ 0, -3, 2],
[ 3, 0, -1],
[-2, 1, 0]])
Output:
np.array([1, 2, 3])
"""
return np.array([so3mat[2][1], so3mat[0][2], so3mat[1][0]])这个函数的作用和VecToso3刚好相反,是把[w]转化为向量表示。
AxisAng3:旋转三维矢量到轴角
def AxisAng3(expc3):
"""Converts a 3-vector of exponential coordinates for rotation into
axis-angle form
:param expc3: A 3-vector of exponential coordinates for rotation
:return omghat: A unit rotation axis
:return theta: The corresponding rotation angle
Example Input:
expc3 = np.array([1, 2, 3])
Output:
(np.array([0.26726124, 0.53452248, 0.80178373]), 3.7416573867739413)
"""
return (Normalize(expc3), np.linalg.norm(expc3))这是一个工具函数,我们可以看到:其作用是:将用于旋转的指数坐标的3维矢量转换为轴角度形式。即返回的第一个数是归一化的方向,第二维是角度。
MatrixExp3:矩阵指数积,so3到旋转矩阵
def MatrixExp3(so3mat):
"""Computes the matrix exponential of a matrix in so(3)
:param so3mat: A 3x3 skew-symmetric matrix
:return: The matrix exponential of so3mat
Example Input:
so3mat = np.array([[ 0, -3, 2],
[ 3, 0, -1],
[-2, 1, 0]])
Output:
np.array([[-0.69492056, 0.71352099, 0.08929286],
[-0.19200697, -0.30378504, 0.93319235],
[ 0.69297817, 0.6313497 , 0.34810748]])
"""
omgtheta = so3ToVec(so3mat)
if NearZero(np.linalg.norm(omgtheta)):
return np.eye(3)
else:
theta = AxisAng3(omgtheta)[1]
omgmat = so3mat / theta
return np.eye(3) + np.sin(theta) * omgmat \
+ (1 - np.cos(theta)) * np.dot(omgmat, omgmat)
从这个函数开始,代码量开始增大,它的作用是:
输入一个反对称矩阵,把它转化为一个旋转矩阵。即我上面在VecToso3部分提到的公式:

即比较著名的罗德里格斯公式。(这个公式友好多种表达形式)
我们可以看到在实现中,我们首先调用了前面提到的so3ToVec,把反对称矩阵中的向量提出来。
在这里我们需要对它做一个安全性的校验:如果它的模长接近于0,即直接返回单位矩阵。否则要计算它的角度。
omgmat = so3mat / theta
我们可以看到有一步这样的操作:首先这个操作是要把[w]给变成标准的归一化反对称矩阵,然后再套用上面的公式来计算旋转矩阵。当角度是0的时候就不能除以了,因此做了一个if 和 else的检查判断。
MatrixLog3:矩阵对数,旋转矩阵到so3
def MatrixLog3(R):
"""Computes the matrix logarithm of a rotation matrix
:param R: A 3x3 rotation matrix
:return: The matrix logarithm of R
Example Input:
R = np.array([[0, 0, 1],
[1, 0, 0],
[0, 1, 0]])
Output:
np.array([[ 0, -1.20919958, 1.20919958],
[ 1.20919958, 0, -1.20919958],
[-1.20919958, 1.20919958, 0]])
"""
acosinput = (np.trace(R) - 1) / 2.0
if acosinput >= 1:
return np.zeros((3, 3))
elif acosinput <= -1:
if not NearZero(1 + R[2][2]):
omg = (1.0 / np.sqrt(2 * (1 + R[2][2]))) \
* np.array([R[0][2], R[1][2], 1 + R[2][2]])
elif not NearZero(1 + R[1][1]):
omg = (1.0 / np.sqrt(2 * (1 + R[1][1]))) \
* np.array([R[0][1], 1 + R[1][1], R[2][1]])
else:
omg = (1.0 / np.sqrt(2 * (1 + R[0][0]))) \
* np.array([1 + R[0][0], R[1][0], R[2][0]])
return VecToso3(np.pi * omg)
else:
theta = np.arccos(acosinput)
return theta / 2.0 / np.sin(theta) * (R - np.array(R).T)这个函数看起来比较复杂了,那么它是要干啥呢?
它会把一个输入的旋转矩阵,转化为so3的矩阵形式。

我们可以分析下代码是如何实现的:
我们首先计算了

在这里代码首先判断:
if acosinput >= 1:
return np.zeros((3, 3))
那这就说明R是一个单位阵(对角线元素都大于等于3了) ,那就返回一个零矩阵即可,模长为0,方向任意。
然后再判断:
elif acosinput <= -1:
即为上图的b的形式:
if not NearZero(1 + R[2][2]):
omg = (1.0 / np.sqrt(2 * (1 + R[2][2]))) \
* np.array([R[0][2], R[1][2], 1 + R[2][2]])
对应

注意这里公式的下标是从1开始,而代码的下标是从0开始。
elif not NearZero(1 + R[1][1]):
omg = (1.0 / np.sqrt(2 * (1 + R[1][1]))) \
* np.array([R[0][1], 1 + R[1][1], R[2][1]])

else:
omg = (1.0 / np.sqrt(2 * (1 + R[0][0]))) \
* np.array([1 + R[0][0], R[1][0], R[2][0]])

注意以上三种算出的都是w向量。根据函数要求,应该返回一个矩阵形式的内容,因此还需要调用一个VecToso3来实现:
return VecToso3(np.pi * omg)
需要谨记的是:

这种情况下,只求一个w是不对的, 因为根据函数的意思是,要把R送入,得到so3,所以里面要有角度相关的变量。这种情况下,theta为pi。因此传入VecToso3的实参是np.pi * omg而不是一个单纯的omg。
最后就是常规情况:
else:
theta = np.arccos(acosinput)
return theta / 2.0 / np.sin(theta) * (R - np.array(R).T)

先求出theta,然后直接根据函数内容得到so3进行返回就可以了。
RpToTrans:旋转平移构造齐次矩阵
def RpToTrans(R, p):
"""Converts a rotation matrix and a position vector into homogeneous
transformation matrix
:param R: A 3x3 rotation matrix
:param p: A 3-vector
:return: A homogeneous transformation matrix corresponding to the inputs
Example Input:
R = np.array([[1, 0, 0],
[0, 0, -1],
[0, 1, 0]])
p = np.array([1, 2, 5])
Output:
np.array([[1, 0, 0, 1],
[0, 0, -1, 2],
[0, 1, 0, 5],
[0, 0, 0, 1]])
"""
return np.r_[np.c_[R, p], [[0, 0, 0, 1]]]这个函数本身没有什么好说,但是发现它的实现方式有些好玩,用到了np.r_和np.c_:
numpy.r_: 将slice对象沿第一轴进行连接(上下拼接)
我们可以看到,在这里,np.r_的括号里分成了两份:
一份是np.c_[R, p],
一份是 [[0, 0, 0, 1]]
那么这俩二维数组,沿第一轴进行连接,即沿着x轴进行拼接。
numpy.c:将slice对象沿第二轴进行连接(左右拼接)
np.c_[R, p]即把R和p左右拼起来。
TransToRp:齐次矩阵拆分旋转平移
def TransToRp(T):
"""Converts a homogeneous transformation matrix into a rotation matrix
and position vector
:param T: A homogeneous transformation matrix
:return R: The corresponding rotation matrix,
:return p: The corresponding position vector.
Example Input:
T = np.array([[1, 0, 0, 0],
[0, 0, -1, 0],
[0, 1, 0, 3],
[0, 0, 0, 1]])
Output:
(np.array([[1, 0, 0],
[0, 0, -1],
[0, 1, 0]]),
np.array([0, 0, 3]))
"""
T = np.array(T)
return T[0: 3, 0: 3], T[0: 3, 3]用到了切片,入门知识,没什么好说的。
TransInv:齐次矩阵的逆矩阵
def TransInv(T):
"""Inverts a homogeneous transformation matrix
:param T: A homogeneous transformation matrix
:return: The inverse of T
Uses the structure of transformation matrices to avoid taking a matrix
inverse, for efficiency.
Example input:
T = np.array([[1, 0, 0, 0],
[0, 0, -1, 0],
[0, 1, 0, 3],
[0, 0, 0, 1]])
Output:
np.array([[1, 0, 0, 0],
[0, 0, 1, -3],
[0, -1, 0, 0],
[0, 0, 0, 1]])
"""
R, p = TransToRp(T)
Rt = np.array(R).T
return np.r_[np.c_[Rt, -np.dot(Rt, p)], [[0, 0, 0, 1]]]
实际在机械臂控制当中,一般都有速度要求,即你的求解必须在机械臂的控制频率内计算得到。例如你的机械臂是1000hz控制频率,那就意味着每个控制周期必须在1ms内计算完成,否则机械臂就会丢包导致不稳定。因此快速计算齐次矩阵的逆矩阵则是非常必要的。
看到代码中又用到了np.r_和np.c_,我们可以辅助记忆,r代表row,即按行拼接。c代表column,代表按列拼接。
VecTose3:向量到se3
def VecTose3(V):
"""Converts a spatial velocity vector into a 4x4 matrix in se3
:param V: A 6-vector representing a spatial velocity
:return: The 4x4 se3 representation of V
Example Input:
V = np.array([1, 2, 3, 4, 5, 6])
Output:
np.array([[ 0, -3, 2, 4],
[ 3, 0, -1, 5],
[-2, 1, 0, 6],
[ 0, 0, 0, 0]])
"""
return np.r_[np.c_[VecToso3([V[0], V[1], V[2]]), [V[3], V[4], V[5]]],
np.zeros((1, 4))]我们知道在旋量理论体系下,是w在前,v在后的:

根据这一套实现可以把旋量的向量转化为se3
se3ToVec:se3到向量
def se3ToVec(se3mat):
""" Converts an se3 matrix into a spatial velocity vector
:param se3mat: A 4x4 matrix in se3
:return: The spatial velocity 6-vector corresponding to se3mat
Example Input:
se3mat = np.array([[ 0, -3, 2, 4],
[ 3, 0, -1, 5],
[-2, 1, 0, 6],
[ 0, 0, 0, 0]])
Output:
np.array([1, 2, 3, 4, 5, 6])
"""
return np.r_[[se3mat[2][1], se3mat[0][2], se3mat[1][0]],
[se3mat[0][3], se3mat[1][3], se3mat[2][3]]]这个就是从[V]中把向量提取出来,和VecTose3为反过程。
Adjoint:计算齐次矩阵的伴随矩阵
def Adjoint(T):
"""Computes the adjoint representation of a homogeneous transformation
matrix
:param T: A homogeneous transformation matrix
:return: The 6x6 adjoint representation [AdT] of T
Example Input:
T = np.array([[1, 0, 0, 0],
[0, 0, -1, 0],
[0, 1, 0, 3],
[0, 0, 0, 1]])
Output:
np.array([[1, 0, 0, 0, 0, 0],
[0, 0, -1, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 3, 1, 0, 0],
[3, 0, 0, 0, 0, -1],
[0, 0, 0, 0, 1, 0]])
"""
R, p = TransToRp(T)
return np.r_[np.c_[R, np.zeros((3, 3))],
np.c_[np.dot(VecToso3(p), R), R]]这个函数即计算伴随矩阵:

我们可以看到现在开始使用到前面所造的轮子了。
既然写到这里了,我们回顾一下,这个伴随矩阵是干嘛用的?

伴随矩阵就是实现两个旋量之间的坐标变换用的。
ScrewToAxis:螺旋轴qsh到标准螺旋轴:
def ScrewToAxis(q, s, h):
"""Takes a parametric description of a screw axis and converts it to a
normalized screw axis
:param q: A point lying on the screw axis
:param s: A unit vector in the direction of the screw axis
:param h: The pitch of the screw axis
:return: A normalized screw axis described by the inputs
Example Input:
q = np.array([3, 0, 0])
s = np.array([0, 0, 1])
h = 2
Output:
np.array([0, 0, 1, 0, -3, 2])
"""
return np.r_[s, np.cross(q, s) + np.dot(h, s)]
我们这里可以回顾一下:
【现代机器人学】学习笔记二:刚体运动
s表示螺旋轴的朝向,\dot{\theta}则表示绕轴转动的角速度大小。(注意这里是dot,上面是有一点的,表示角度的导数,角速度)。
h表示节距,即线速度/角速度。
q为轴上任意一点,用于配合s定位这根轴。
那么代码里的S和这里的旋量v,其实代表了S是V的一个正则化。
即满足条件:
AxisAng6:旋量到螺旋轴的正则化过程
def AxisAng6(expc6):
"""Converts a 6-vector of exponential coordinates into screw axis-angle
form
:param expc6: A 6-vector of exponential coordinates for rigid-body motion
S*theta
:return S: The corresponding normalized screw axis
:return theta: The distance traveled along/about S
Example Input:
expc6 = np.array([1, 0, 0, 1, 2, 3])
Output:
(np.array([1.0, 0.0, 0.0, 1.0, 2.0, 3.0]), 1.0)
"""
theta = np.linalg.norm([expc6[0], expc6[1], expc6[2]])
if NearZero(theta):
theta = np.linalg.norm([expc6[3], expc6[4], expc6[5]])
return (np.array(expc6 / theta), theta)我们注意到代码中,先把前三个数字做了二范数,即判断角速度的模长是否接近0。然后才做后续的步骤:
这个函数的描述是,对6维指数坐标转化为螺旋轴表示形式:
其实这是描述了一个旋量到螺旋轴的正则化过程。
MatrixExp6:se3到齐次矩阵
def MatrixExp6(se3mat):
"""Computes the matrix exponential of an se3 representation of
exponential coordinates
:param se3mat: A matrix in se3
:return: The matrix exponential of se3mat
Example Input:
se3mat = np.array([[0, 0, 0, 0],
[0, 0, -1.57079632, 2.35619449],
[0, 1.57079632, 0, 2.35619449],
[0, 0, 0, 0]])
Output:
np.array([[1.0, 0.0, 0.0, 0.0],
[0.0, 0.0, -1.0, 0.0],
[0.0, 1.0, 0.0, 3.0],
[ 0, 0, 0, 1]])
"""
se3mat = np.array(se3mat)
omgtheta = so3ToVec(se3mat[0: 3, 0: 3])
if NearZero(np.linalg.norm(omgtheta)):
return np.r_[np.c_[np.eye(3), se3mat[0: 3, 3]], [[0, 0, 0, 1]]]
else:
theta = AxisAng3(omgtheta)[1]
omgmat = se3mat[0: 3, 0: 3] / theta
return np.r_[np.c_[MatrixExp3(se3mat[0: 3, 0: 3]),
np.dot(np.eye(3) * theta \
+ (1 - np.cos(theta)) * omgmat \
+ (theta - np.sin(theta)) \
* np.dot(omgmat,omgmat),
se3mat[0: 3, 3]) / theta],
[[0, 0, 0, 1]]]送入一个se3:

求解下面的内容:

我们首先要判断角速度是不是0,如果是的话,那角度就是0,即省去很多计算:
if NearZero(np.linalg.norm(omgtheta)):
return np.r_[np.c_[np.eye(3), se3mat[0: 3, 3]], [[0, 0, 0, 1]]]
否则的话我们得先老老实实求出so3和对应角度:
theta = AxisAng3(omgtheta)[1]
omgmat = se3mat[0: 3, 0: 3] / theta
然后套用上面的公式来求齐次矩阵:
return np.r_[np.c_[MatrixExp3(se3mat[0: 3, 0: 3]),
np.dot(np.eye(3) * theta \
+ (1 - np.cos(theta)) * omgmat \
+ (theta - np.sin(theta)) \
* np.dot(omgmat,omgmat),
se3mat[0: 3, 3]) / theta],
[[0, 0, 0, 1]]]
我们观察到,左上角:
MatrixExp3(se3mat[0: 3, 0: 3]) 调用MatrixExp3把so3转换为旋转矩阵
然后右上角
np.dot(np.eye(3) * theta \
+ (1 - np.cos(theta)) * omgmat \
+ (theta - np.sin(theta)) \
* np.dot(omgmat,omgmat),
se3mat[0: 3, 3]) / theta
代表两项,由
np.eye(3) * theta \
+ (1 - np.cos(theta)) * omgmat \
+ (theta - np.sin(theta)) \
* np.dot(omgmat,omgmat)
和 se3mat[0: 3, 3]) / theta 进行点乘。
前者代表:

后者代表v,注意,在这个公式当中,w的模长为1,或w=0,v的模长为1。这也就是为什么se3mat[0: 3, 3]) / theta 代表v。
那么这里的theta是通过调用AxisAng3得到的,注意我们这里的这个case,已经是w不为0的case了。
MatrixLog6:齐次矩阵到se3
def MatrixLog6(T):
"""Computes the matrix logarithm of a homogeneous transformation matrix
:param R: A matrix in SE3
:return: The matrix logarithm of R
Example Input:
T = np.array([[1, 0, 0, 0],
[0, 0, -1, 0],
[0, 1, 0, 3],
[0, 0, 0, 1]])
Output:
np.array([[0, 0, 0, 0]
[0, 0, -1.57079633, 2.35619449]
[0, 1.57079633, 0, 2.35619449]
[0, 0, 0, 0]])
"""
R, p = TransToRp(T)
omgmat = MatrixLog3(R)
if np.array_equal(omgmat, np.zeros((3, 3))):
return np.r_[np.c_[np.zeros((3, 3)),
[T[0][3], T[1][3], T[2][3]]],
[[0, 0, 0, 0]]]
else:
theta = np.arccos((np.trace(R) - 1) / 2.0)
return np.r_[np.c_[omgmat,
np.dot(np.eye(3) - omgmat / 2.0 \
+ (1.0 / theta - 1.0 / np.tan(theta / 2.0) / 2) \
* np.dot(omgmat,omgmat) / theta,[T[0][3],
T[1][3],
T[2][3]])],
[[0, 0, 0, 0]]]我们可以看到这个函数的注释是作者偷懒了,他拷贝来的,return还是MatrixLog3的内容。。
言归正传:

这个实现看起来比较复杂,我们拆开来看一下:
R, p = TransToRp(T)
omgmat = MatrixLog3(R)
是从齐次矩阵得到的旋转和平移,然后把旋转直接用之前的函数MatrixLog3求了一个so3出来。
随后,要判断这个旋转矩阵是不是单位阵:
if np.array_equal(omgmat, np.zeros((3, 3))):
return np.r_[np.c_[np.zeros((3, 3)),
[T[0][3], T[1][3], T[2][3]]],
[[0, 0, 0, 0]]]
他的实现是判断so3是不是各项都为0,当然我们自己实现的时候也可以判断轴角的角度是不是0,或者三个轴是不是都为0,这个实现可以多种。
如果是的话,那得到的[v]中的[w]就都是0,v的话直接取平移部分的值。
这里要注意:

这里得到的w和v,其实是螺旋轴[S]里的表示。
我们这里一定要分清楚:
se3指的是 中的红色部分,因此是有theta项的。
中的红色部分,因此是有theta项的。
同理前面的MatrixLog3函数的返回值中,也是有一项是theta项的。(接下来也要注意这句话!!)
所以接下来后面注意,返回值得到的[S]以后,也要和theta相乘才是真正的se3的结果!
接下来我们再看当旋转不为0的情况:
theta = np.arccos((np.trace(R) - 1) / 2.0)
return np.r_[np.c_[omgmat,
np.dot(np.eye(3) - omgmat / 2.0 \
+ (1.0 / theta - 1.0 / np.tan(theta / 2.0) / 2) \
* np.dot(omgmat,omgmat) / theta,[T[0][3],
T[1][3],
T[2][3]])],
[[0, 0, 0, 0]]]
omgmat代表[w]theta, 然后在列上做一个拼接,和v*theta拼接到一起。
v怎么得到呢?

v*theta 即
np.dot(np.eye(3) - omgmat / 2.0 \
+ (1.0 / theta - 1.0 / np.tan(theta / 2.0) / 2) \
* np.dot(omgmat,omgmat) / theta,[T[0][3],
T[1][3],
T[2][3]])],
其中,p则是
[T[0][3], T[1][3], T[2][3]])],
而

第一项,np.eye(3)代表1/theta * I * theta, 我们知道theta是一个标量,可以直接乘进去
第二项,因为我们的omgmat是从MatrixLog3(R)得到的,因此omgmat这一项代表了[w]* theta,所以 omgmat / 2.0代表了 1/2 *[w] *theta
我们再看第三项,
 这一项再乘以theta对应:
这一项再乘以theta对应:
(1.0 / theta - 1.0 / np.tan(theta / 2.0) / 2) * np.dot(omgmat,omgmat) / theta
这是怎么得到的呢?
注意,omgmat实际上是[w]theta,因此np.dot(omgmat,omgmat)实际上变成了[w]^2 \theta^2,所以要多除以一个theta!
ProjectToSO3:找到和SO3最近的矩阵
def ProjectToSO3(mat):
"""Returns a projection of mat into SO(3)
:param mat: A matrix near SO(3) to project to SO(3)
:return: The closest matrix to R that is in SO(3)
Projects a matrix mat to the closest matrix in SO(3) using singular-value
decomposition (see
http://hades.mech.northwestern.edu/index.php/Modern_Robotics_Linear_Algebra_Review).
This function is only appropriate for matrices close to SO(3).
Example Input:
mat = np.array([[ 0.675, 0.150, 0.720],
[ 0.370, 0.771, -0.511],
[-0.630, 0.619, 0.472]])
Output:
np.array([[ 0.67901136, 0.14894516, 0.71885945],
[ 0.37320708, 0.77319584, -0.51272279],
[-0.63218672, 0.61642804, 0.46942137]])
"""
U, s, Vh = np.linalg.svd(mat)
R = np.dot(U, Vh)
if np.linalg.det(R) < 0:
# In this case the result may be far from mat.
R[:, 2] = -R[:, 2]
return R这个函数的作用是,我们可能会经常对一些旋转矩阵进行不同形式的转换(例如轴角,四元数等),那这就可能导致精度的损失,以至于这个矩阵不再是SO3的形式。这个函数书上并没有提到,这是一个工程中用到的方法,所以需要参考这个附录:
http://hades.mech.northwestern.edu/images/c/c8/AppendixE-linear-algebra-review-Dec20-2019.pdf因为R是正交矩阵,所以奇异值分解以后,中间的奇异值矩阵应该是1。对于不是1的情况,只要把它认为是1即可。

当然,这样可能存在的问题是,输入的矩阵可能行列式是-1,这种实际上说明它不在SO3空间中,那简单的处理方法是把最后一列取反。不过这样的话,输出的矩阵就和输入的差很多了。
ProjectToSE3:找到和SE3最接近的矩阵
def ProjectToSE3(mat):
"""Returns a projection of mat into SE(3)
:param mat: A 4x4 matrix to project to SE(3)
:return: The closest matrix to T that is in SE(3)
Projects a matrix mat to the closest matrix in SE(3) using singular-value
decomposition (see
http://hades.mech.northwestern.edu/index.php/Modern_Robotics_Linear_Algebra_Review).
This function is only appropriate for matrices close to SE(3).
Example Input:
mat = np.array([[ 0.675, 0.150, 0.720, 1.2],
[ 0.370, 0.771, -0.511, 5.4],
[-0.630, 0.619, 0.472, 3.6],
[ 0.003, 0.002, 0.010, 0.9]])
Output:
np.array([[ 0.67901136, 0.14894516, 0.71885945, 1.2 ],
[ 0.37320708, 0.77319584, -0.51272279, 5.4 ],
[-0.63218672, 0.61642804, 0.46942137, 3.6 ],
[ 0. , 0. , 0. , 1. ]])
"""
mat = np.array(mat)
return RpToTrans(ProjectToSO3(mat[:3, :3]), mat[:3, 3])这个函数一看就懂,我们知道这个事情麻烦就麻烦在左上角的旋转矩阵当中,我们只要调用上一个函数ProjectToSO3,把输入矩阵的旋转部分做一个投影,平移部分直接抄下来,就可以了。
DistanceToSO3:计算距离SO3的距离
def DistanceToSO3(mat):
"""Returns the Frobenius norm to describe the distance of mat from the
SO(3) manifold
:param mat: A 3x3 matrix
:return: A quantity describing the distance of mat from the SO(3)
manifold
Computes the distance from mat to the SO(3) manifold using the following
method:
If det(mat) <= 0, return a large number.
If det(mat) > 0, return norm(mat^T.mat - I).
Example Input:
mat = np.array([[ 1.0, 0.0, 0.0 ],
[ 0.0, 0.1, -0.95],
[ 0.0, 1.0, 0.1 ]])
Output:
0.08835
"""
if np.linalg.det(mat) > 0:
return np.linalg.norm(np.dot(np.array(mat).T, mat) - np.eye(3))
else:
return 1e+9如果行列式小于等于0,说明它就不是SO3,这时候直接返回一个很大的值即可。
否则,我们要利用SO3的一个特性:即它是正交矩阵。因此我们把这个矩阵和它的转置乘起来,看看是不是单位阵,并且把它和单位阵相减,计算二范数,即可得到距离SO3的距离。
DistanceToSE3:计算距离SE3的距离
def DistanceToSE3(mat):
"""Returns the Frobenius norm to describe the distance of mat from the
SE(3) manifold
:param mat: A 4x4 matrix
:return: A quantity describing the distance of mat from the SE(3)
manifold
Computes the distance from mat to the SE(3) manifold using the following
method:
Compute the determinant of matR, the top 3x3 submatrix of mat.
If det(matR) <= 0, return a large number.
If det(matR) > 0, replace the top 3x3 submatrix of mat with matR^T.matR,
and set the first three entries of the fourth column of mat to zero. Then
return norm(mat - I).
Example Input:
mat = np.array([[ 1.0, 0.0, 0.0, 1.2 ],
[ 0.0, 0.1, -0.95, 1.5 ],
[ 0.0, 1.0, 0.1, -0.9 ],
[ 0.0, 0.0, 0.1, 0.98 ]])
Output:
0.134931
"""
matR = np.array(mat)[0: 3, 0: 3]
if np.linalg.det(matR) > 0:
return np.linalg.norm(np.r_[np.c_[np.dot(np.transpose(matR), matR),
np.zeros((3, 1))],
[np.array(mat)[3, :]]] - np.eye(4))
else:
return 1e+9我们的判断依据仍然是,以旋转部分作为判断,如果旋转部分的行列式都小于等于0,那返回大值;否则和DistanceToSO3那样照猫画虎拼一个像单位阵的东西 ,与单位阵相减,计算二范数即可。
TestIfSO3:检查输入矩阵是否是SO3
def TestIfSO3(mat):
"""Returns true if mat is close to or on the manifold SO(3)
:param mat: A 3x3 matrix
:return: True if mat is very close to or in SO(3), false otherwise
Computes the distance d from mat to the SO(3) manifold using the
following method:
If det(mat) <= 0, d = a large number.
If det(mat) > 0, d = norm(mat^T.mat - I).
If d is close to zero, return true. Otherwise, return false.
Example Input:
mat = np.array([[1.0, 0.0, 0.0 ],
[0.0, 0.1, -0.95],
[0.0, 1.0, 0.1 ]])
Output:
False
"""
return abs(DistanceToSO3(mat)) < 1e-3我们调用上面得到的DistanceToSO3就可以轻易得到输入矩阵和SO3的距离从而进行判断。
TestIfSE3:检查输入矩阵是否是SE3
def TestIfSE3(mat):
"""Returns true if mat is close to or on the manifold SE(3)
:param mat: A 4x4 matrix
:return: True if mat is very close to or in SE(3), false otherwise
Computes the distance d from mat to the SE(3) manifold using the
following method:
Compute the determinant of the top 3x3 submatrix of mat.
If det(mat) <= 0, d = a large number.
If det(mat) > 0, replace the top 3x3 submatrix of mat with mat^T.mat, and
set the first three entries of the fourth column of mat to zero.
Then d = norm(T - I).
If d is close to zero, return true. Otherwise, return false.
Example Input:
mat = np.array([[1.0, 0.0, 0.0, 1.2],
[0.0, 0.1, -0.95, 1.5],
[0.0, 1.0, 0.1, -0.9],
[0.0, 0.0, 0.1, 0.98]])
Output:
False
"""
return abs(DistanceToSE3(mat)) < 1e-3
这个和上一个类似,就不多说了。注意平时实用的时候,记得判断输入矩阵的大小,这是作者没有做的。如果输入矩阵不一样大,就会报错了,而不是正常返回true或false。
机器人运动学部分:
FKinBody:基于Body系进行FK计算
def FKinBody(M, Blist, thetalist):
"""Computes forward kinematics in the body frame for an open chain robot
:param M: The home configuration (position and orientation) of the end-
effector
:param Blist: The joint screw axes in the end-effector frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param thetalist: A list of joint coordinates
:return: A homogeneous transformation matrix representing the end-
effector frame when the joints are at the specified coordinates
(i.t.o Body Frame)
Example Input:
M = np.array([[-1, 0, 0, 0],
[ 0, 1, 0, 6],
[ 0, 0, -1, 2],
[ 0, 0, 0, 1]])
Blist = np.array([[0, 0, -1, 2, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0.1]]).T
thetalist = np.array([np.pi / 2.0, 3, np.pi])
Output:
np.array([[0, 1, 0, -5],
[1, 0, 0, 4],
[0, 0, -1, 1.68584073],
[0, 0, 0, 1]])
"""
T = np.array(M)
for i in range(len(thetalist)):
T = np.dot(T, MatrixExp6(VecTose3(np.array(Blist)[:, i] \
* thetalist[i])))
return T这个函数可以参考我们FK这节的实现内容:

我们可以看到,输入的M是机械臂在0位置时,末端的姿态;
B则是我们根据旋量的表述,以body系作为参考,各个轴的螺旋轴表示:
【现代机器人学】学习笔记三:前向运动学(Forward Kinematics)
而theta则是各个关节角的执行角度。
我们可以注意到,因为是在body系下的操作,因此按顺序写在M的右侧。
FKinSpace:基于Space系进行FK计算
def FKinSpace(M, Slist, thetalist):
"""Computes forward kinematics in the space frame for an open chain robot
:param M: The home configuration (position and orientation) of the end-
effector
:param Slist: The joint screw axes in the space frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param thetalist: A list of joint coordinates
:return: A homogeneous transformation matrix representing the end-
effector frame when the joints are at the specified coordinates
(i.t.o Space Frame)
Example Input:
M = np.array([[-1, 0, 0, 0],
[ 0, 1, 0, 6],
[ 0, 0, -1, 2],
[ 0, 0, 0, 1]])
Slist = np.array([[0, 0, 1, 4, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, -1, -6, 0, -0.1]]).T
thetalist = np.array([np.pi / 2.0, 3, np.pi])
Output:
np.array([[0, 1, 0, -5],
[1, 0, 0, 4],
[0, 0, -1, 1.68584073],
[0, 0, 0, 1]])
"""
T = np.array(M)
for i in range(len(thetalist) - 1, -1, -1):
T = np.dot(MatrixExp6(VecTose3(np.array(Slist)[:, i] \
* thetalist[i])), T)
return T
这个函数我们参考基于Space的指数积公式:

实现的方法也和上一个函数,FKinBody类似,先把机械臂摆到零位,然后输入各个轴在space系下的螺旋轴的表示,以及转过的角度。因为是基于Space系进行的操作,因此放到M的左侧,顺序则与Body系下的类似操作相同。不过从代码实现上,是倒着乘的,因此实现上也是倒着来。
JacobianSpace:基于Space系的机器人雅可比
def JacobianSpace(Slist, thetalist):
"""Computes the space Jacobian for an open chain robot
:param Slist: The joint screw axes in the space frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param thetalist: A list of joint coordinates
:return: The space Jacobian corresponding to the inputs (6xn real
numbers)
Example Input:
Slist = np.array([[0, 0, 1, 0, 0.2, 0.2],
[1, 0, 0, 2, 0, 3],
[0, 1, 0, 0, 2, 1],
[1, 0, 0, 0.2, 0.3, 0.4]]).T
thetalist = np.array([0.2, 1.1, 0.1, 1.2])
Output:
np.array([[ 0, 0.98006658, -0.09011564, 0.95749426]
[ 0, 0.19866933, 0.4445544, 0.28487557]
[ 1, 0, 0.89120736, -0.04528405]
[ 0, 1.95218638, -2.21635216, -0.51161537]
[0.2, 0.43654132, -2.43712573, 2.77535713]
[0.2, 2.96026613, 3.23573065, 2.22512443]])
"""
Js = np.array(Slist).copy().astype(float)
T = np.eye(4)
for i in range(1, len(thetalist)):
T = np.dot(T, MatrixExp6(VecTose3(np.array(Slist)[:, i - 1] \
* thetalist[i - 1])))
Js[:, i] = np.dot(Adjoint(T), np.array(Slist)[:, i])
return Js我们看先回忆一下,基于Space系的机器人雅可比如何计算:
先把机器人依次从1轴开始,摆到某个位形(在FK中是0位,这里则不是零位),然后根据坐标系的朝向写出下一个轴(第i轴)的w,然后把轴上一点q也写出来,使用-w \times q 写出v,或者直接根据移动副写出v,令w为0。这样就写出来就是雅可比中的i列。
1.对于第一轴,和FK中算螺旋轴旋量的方法一样。
2.对于当前的w和q,要考虑进去前面的旋转和平移,可以写成变量的形式。
————————————————
版权声明:本文为CSDN博主「zkk9527」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/zkk9527/article/details/128278741

我们现在细看这个代码:
for i in range(1, len(thetalist)):
T = np.dot(T, MatrixExp6(VecTose3(np.array(Slist)[:, i - 1] \
* thetalist[i - 1]))) 这一步操作是为了逐步得到 ,因为公式中,是乘到i-1截止,并且从2开始;
,因为公式中,是乘到i-1截止,并且从2开始;
因此代码的实现上,从1开始乘(因为代码下标是从0开始), 雅可比的第0列和S螺旋轴保持一致,而从第一列开始(即下标为i),先通过VectorTose3得到[Si],再乘以对应的角度,再通过MatrixExp6得到具体的指数积,并和之前的累乘。
详细看:对于公式中的i=2(代码中则为i=1),带入公式则只有第一项 ,由于要套用这个累乘的框架,因此T先要置为单位矩阵。
,由于要套用这个累乘的框架,因此T先要置为单位矩阵。
然后调用Ad函数,求其伴随矩阵,并和第i列的螺旋轴相乘:
Js[:, i] = np.dot(Adjoint(T), np.array(Slist)[:, i])从而得到第i列的机器人雅可比,实现如下操作

JacobianBody:基于Body系的机器人雅可比
def JacobianBody(Blist, thetalist):
"""Computes the body Jacobian for an open chain robot
:param Blist: The joint screw axes in the end-effector frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param thetalist: A list of joint coordinates
:return: The body Jacobian corresponding to the inputs (6xn real
numbers)
Example Input:
Blist = np.array([[0, 0, 1, 0, 0.2, 0.2],
[1, 0, 0, 2, 0, 3],
[0, 1, 0, 0, 2, 1],
[1, 0, 0, 0.2, 0.3, 0.4]]).T
thetalist = np.array([0.2, 1.1, 0.1, 1.2])
Output:
np.array([[-0.04528405, 0.99500417, 0, 1]
[ 0.74359313, 0.09304865, 0.36235775, 0]
[-0.66709716, 0.03617541, -0.93203909, 0]
[ 2.32586047, 1.66809, 0.56410831, 0.2]
[-1.44321167, 2.94561275, 1.43306521, 0.3]
[-2.06639565, 1.82881722, -1.58868628, 0.4]])
"""
Jb = np.array(Blist).copy().astype(float)
T = np.eye(4)
for i in range(len(thetalist) - 2, -1, -1):
T = np.dot(T,MatrixExp6(VecTose3(np.array(Blist)[:, i + 1] \
* -thetalist[i + 1])))
Jb[:, i] = np.dot(Adjoint(T), np.array(Blist)[:, i])
return Jb基于Body系的雅克比,则也是类似,我们需要参考body系的雅可比计算方法:

我们围绕这个公式入手:

for i in range(len(thetalist) - 2, -1, -1):
T = np.dot(T,MatrixExp6(VecTose3(np.array(Blist)[:, i + 1] \
* -thetalist[i + 1])))这一步的操作是为了计算:

我们可以注意,原公式是从n-1开始计算,那么在代码中,由于下标为0开始,因此公式中的n-1实际上就是代码中的n-2;
我们按照公式,调用VecTose3得到[Bi+1],再和负数角度相乘,并调用MatrixExp6变成矩阵,一路乘到右侧。
详细看:对于公式中的第一轮,i=n-1(对应代码则是i=n-2),第一项实际上就只有 这一项,由于要套用累乘框架,因此T先要置为单位矩阵。
这一项,由于要套用累乘框架,因此T先要置为单位矩阵。
然后调用Ad函数,求其伴随矩阵,并和第i列的螺旋轴相乘:
Jb[:, i] = np.dot(Adjoint(T), np.array(Blist)[:, i])从而得到第i列的机器人雅可比:

IKinSpace:基于Space系的机器人逆运动学
def IKinSpace(Slist, M, T, thetalist0, eomg, ev):
"""Computes inverse kinematics in the space frame for an open chain robot
:param Slist: The joint screw axes in the space frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param M: The home configuration of the end-effector
:param T: The desired end-effector configuration Tsd
:param thetalist0: An initial guess of joint angles that are close to
satisfying Tsd
:param eomg: A small positive tolerance on the end-effector orientation
error. The returned joint angles must give an end-effector
orientation error less than eomg
:param ev: A small positive tolerance on the end-effector linear position
error. The returned joint angles must give an end-effector
position error less than ev
:return thetalist: Joint angles that achieve T within the specified
tolerances,
:return success: A logical value where TRUE means that the function found
a solution and FALSE means that it ran through the set
number of maximum iterations without finding a solution
within the tolerances eomg and ev.
Uses an iterative Newton-Raphson root-finding method.
The maximum number of iterations before the algorithm is terminated has
been hardcoded in as a variable called maxiterations. It is set to 20 at
the start of the function, but can be changed if needed.
Example Input:
Slist = np.array([[0, 0, 1, 4, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, -1, -6, 0, -0.1]]).T
M = np.array([[-1, 0, 0, 0],
[ 0, 1, 0, 6],
[ 0, 0, -1, 2],
[ 0, 0, 0, 1]])
T = np.array([[0, 1, 0, -5],
[1, 0, 0, 4],
[0, 0, -1, 1.6858],
[0, 0, 0, 1]])
thetalist0 = np.array([1.5, 2.5, 3])
eomg = 0.01
ev = 0.001
Output:
(np.array([ 1.57073783, 2.99966384, 3.1415342 ]), True)
"""
thetalist = np.array(thetalist0).copy()
i = 0
maxiterations = 20
Tsb = FKinSpace(M,Slist, thetalist)
Vs = np.dot(Adjoint(Tsb), \
se3ToVec(MatrixLog6(np.dot(TransInv(Tsb), T))))
err = np.linalg.norm([Vs[0], Vs[1], Vs[2]]) > eomg \
or np.linalg.norm([Vs[3], Vs[4], Vs[5]]) > ev
while err and i < maxiterations:
thetalist = thetalist \
+ np.dot(np.linalg.pinv(JacobianSpace(Slist, \
thetalist)), Vs)
i = i + 1
Tsb = FKinSpace(M, Slist, thetalist)
Vs = np.dot(Adjoint(Tsb), \
se3ToVec(MatrixLog6(np.dot(TransInv(Tsb), T))))
err = np.linalg.norm([Vs[0], Vs[1], Vs[2]]) > eomg \
or np.linalg.norm([Vs[3], Vs[4], Vs[5]]) > ev
return (thetalist, not err)这个函数作为基于Space系的逆解函数,实现从笛卡尔空间到关节空间的映射。
我们先拆分这部分代码,先看输入:
Slist:照例,是space系作为参考的各个螺旋轴的表示;
M:机器人在零位时末端执行器的位形;
T:期望拿来求逆解的笛卡尔位姿;
thetalist0:关节角迭代初值;
eomg:求解的角度的误差应低于此值;
ev:求解的位置误差应低于此值
两个返回值:第一项:求出的运动学逆解; 第二项:是否求解成功
我们先看循环外的操作:
thetalist = np.array(thetalist0).copy()
i = 0
maxiterations = 20
Tsb = FKinSpace(M,Slist, thetalist)
Vs = np.dot(Adjoint(Tsb), \
se3ToVec(MatrixLog6(np.dot(TransInv(Tsb), T))))
err = np.linalg.norm([Vs[0], Vs[1], Vs[2]]) > eomg \
or np.linalg.norm([Vs[3], Vs[4], Vs[5]]) > ev这里对迭代步长进行了硬编码,设置为20次。实际上还有一些其他的技巧自动计算迭代步长,这些小trick可以使得ik可以求解的更好,这个后续我会在其他文章中进行补充。
首先,我们通过FKinSpace进行了前向运动学,那么后面我们该怎么做呢?
直观上说,我们就需要把算出的FK的结果,和期望的笛卡尔位姿,算一个差异值,并且用旋量表示。因此,需要先通过TransInv(Tsb)快速求出逆解,然后和期望的笛卡尔位姿T做一个点乘,算出二者的差异的矩阵ΔT。
然后把这个ΔT,通过MatrixLog6函数,变成旋量se3的矩阵表示 [V],下一步就是调用se3ToVec把它的括号去掉,得到V。
在得到了V以后呢,我们可以注意到,期望的位姿T,其实是Tsd;然后Tsb的逆矩阵Tbs,左乘Tsd,得到了一个Tbd,那么这个Tbd转化为旋量以后,实际上就是基于Body系的旋量Vb,通过伴随矩阵,可以转换到space系下Vs。
在得到space系下的旋量,判断前三维是不是大于容忍的角度误差,后三维是不是大于容忍的位置误差,从而得到一个求解的初始成功与否的变量err。如果有一个大于,则认为求解没成功。
然后我们再看循环里的操作:
while err and i < maxiterations:
thetalist = thetalist \
+ np.dot(np.linalg.pinv(JacobianSpace(Slist, \
thetalist)), Vs)
i = i + 1
Tsb = FKinSpace(M, Slist, thetalist)
Vs = np.dot(Adjoint(Tsb), \
se3ToVec(MatrixLog6(np.dot(TransInv(Tsb), T))))
err = np.linalg.norm([Vs[0], Vs[1], Vs[2]]) > eomg \
or np.linalg.norm([Vs[3], Vs[4], Vs[5]]) > ev后面的几行之前的一样,就不讲了。在这里我们只分析前面的梯度变化的过程:
thetalist = thetalist \
+ np.dot(np.linalg.pinv(JacobianSpace(Slist, \
thetalist)), Vs) 
我们根据公式来看,一目了然。
最后把求得的关节角,以及成功与否的变量返回回去即可。
IKinBody:基于Body系的机器人逆运动学
def IKinBody(Blist, M, T, thetalist0, eomg, ev):
"""Computes inverse kinematics in the body frame for an open chain robot
:param Blist: The joint screw axes in the end-effector frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param M: The home configuration of the end-effector
:param T: The desired end-effector configuration Tsd
:param thetalist0: An initial guess of joint angles that are close to
satisfying Tsd
:param eomg: A small positive tolerance on the end-effector orientation
error. The returned joint angles must give an end-effector
orientation error less than eomg
:param ev: A small positive tolerance on the end-effector linear position
error. The returned joint angles must give an end-effector
position error less than ev
:return thetalist: Joint angles that achieve T within the specified
tolerances,
:return success: A logical value where TRUE means that the function found
a solution and FALSE means that it ran through the set
number of maximum iterations without finding a solution
within the tolerances eomg and ev.
Uses an iterative Newton-Raphson root-finding method.
The maximum number of iterations before the algorithm is terminated has
been hardcoded in as a variable called maxiterations. It is set to 20 at
the start of the function, but can be changed if needed.
Example Input:
Blist = np.array([[0, 0, -1, 2, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0.1]]).T
M = np.array([[-1, 0, 0, 0],
[ 0, 1, 0, 6],
[ 0, 0, -1, 2],
[ 0, 0, 0, 1]])
T = np.array([[0, 1, 0, -5],
[1, 0, 0, 4],
[0, 0, -1, 1.6858],
[0, 0, 0, 1]])
thetalist0 = np.array([1.5, 2.5, 3])
eomg = 0.01
ev = 0.001
Output:
(np.array([1.57073819, 2.999667, 3.14153913]), True)
"""
thetalist = np.array(thetalist0).copy()
i = 0
maxiterations = 20
Vb = se3ToVec(MatrixLog6(np.dot(TransInv(FKinBody(M, Blist, \
thetalist)), T)))
err = np.linalg.norm([Vb[0], Vb[1], Vb[2]]) > eomg \
or np.linalg.norm([Vb[3], Vb[4], Vb[5]]) > ev
while err and i < maxiterations:
thetalist = thetalist \
+ np.dot(np.linalg.pinv(JacobianBody(Blist, \
thetalist)), Vb)
i = i + 1
Vb \
= se3ToVec(MatrixLog6(np.dot(TransInv(FKinBody(M, Blist, \
thetalist)), T)))
err = np.linalg.norm([Vb[0], Vb[1], Vb[2]]) > eomg \
or np.linalg.norm([Vb[3], Vb[4], Vb[5]]) > ev
return (thetalist, not err)相比IKinSpace函数,这个函数基本长的一样,不过有两点可以注意:
Vb = se3ToVec(MatrixLog6(np.dot(TransInv(FKinBody(M, Blist, \
thetalist)), T)))针对这个函数,首先调用FKinBody,计算FK。那么这个FK计算出的结果,是Tsb。T则是Tsd,(d意为desired),因此Tsb的逆矩阵Tbs,左乘Tsd,得到的ΔT即Tbd,就是body系下的位姿误差,我们转换为旋量以后,就是[Vb]了。因为这个函数是基于Body系的机器人逆运动学,因此不需要像IKinSpace函数一样还得再调用Adjoint函数转换旋量坐标系。
其他的内容和IKinSpace函数一致,这里不再赘述。
机器人动力学部分:
ad: 旋量李括号(叉积伴随运算)
def ad(V):
"""Calculate the 6x6 matrix [adV] of the given 6-vector
:param V: A 6-vector spatial velocity
:return: The corresponding 6x6 matrix [adV]
Used to calculate the Lie bracket [V1, V2] = [adV1]V2
Example Input:
V = np.array([1, 2, 3, 4, 5, 6])
Output:
np.array([[ 0, -3, 2, 0, 0, 0],
[ 3, 0, -1, 0, 0, 0],
[-2, 1, 0, 0, 0, 0],
[ 0, -6, 5, 0, -3, 2],
[ 6, 0, -4, 3, 0, -1],
[-5, 4, 0, -2, 1, 0]])
"""
omgmat = VecToso3([V[0], V[1], V[2]])
return np.r_[np.c_[omgmat, np.zeros((3, 3))],
np.c_[VecToso3([V[3], V[4], V[5]]), omgmat]]关于这个小的ad,我们要和大的Adjoint函数分开:
在这里我们再回顾一下大的Ad和小的ad的区别:
大Ad表示伴随,是基于矩阵的:
提供一个矩阵,可以计算这样的结果,实现旋量的坐标系转换。
小的ad也表示伴随,是
这个运算再乘以一个旋量意味着两个旋量在做叉积。
InverseDynamics:逆动力学算法
def InverseDynamics(thetalist, dthetalist, ddthetalist, g, Ftip, Mlist, \
Glist, Slist):
"""Computes inverse dynamics in the space frame for an open chain robot
:param thetalist: n-vector of joint variables
:param dthetalist: n-vector of joint rates
:param ddthetalist: n-vector of joint accelerations
:param g: Gravity vector g
:param Ftip: Spatial force applied by the end-effector expressed in frame
{n+1}
:param Mlist: List of link frames {i} relative to {i-1} at the home
position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:return: The n-vector of required joint forces/torques
This function uses forward-backward Newton-Euler iterations to solve the
equation:
taulist = Mlist(thetalist)ddthetalist + c(thetalist,dthetalist) \
+ g(thetalist) + Jtr(thetalist)Ftip
Example Input (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
ddthetalist = np.array([2, 1.5, 1])
g = np.array([0, 0, -9.8])
Ftip = np.array([1, 1, 1, 1, 1, 1])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
Output:
np.array([74.69616155, -33.06766016, -3.23057314])
"""
n = len(thetalist)
Mi = np.eye(4)
Ai = np.zeros((6, n))
AdTi = [[None]] * (n + 1)
Vi = np.zeros((6, n + 1))
Vdi = np.zeros((6, n + 1))
Vdi[:, 0] = np.r_[[0, 0, 0], -np.array(g)]
AdTi[n] = Adjoint(TransInv(Mlist[n]))
Fi = np.array(Ftip).copy()
taulist = np.zeros(n)
for i in range(n):
Mi = np.dot(Mi,Mlist[i])
Ai[:, i] = np.dot(Adjoint(TransInv(Mi)), np.array(Slist)[:, i])
AdTi[i] = Adjoint(np.dot(MatrixExp6(VecTose3(Ai[:, i] * \
-thetalist[i])), \
TransInv(Mlist[i])))
Vi[:, i + 1] = np.dot(AdTi[i], Vi[:,i]) + Ai[:, i] * dthetalist[i]
Vdi[:, i + 1] = np.dot(AdTi[i], Vdi[:, i]) \
+ Ai[:, i] * ddthetalist[i] \
+ np.dot(ad(Vi[:, i + 1]), Ai[:, i]) * dthetalist[i]
for i in range (n - 1, -1, -1):
Fi = np.dot(np.array(AdTi[i + 1]).T, Fi) \
+ np.dot(np.array(Glist[i]), Vdi[:, i + 1]) \
- np.dot(np.array(ad(Vi[:, i + 1])).T, \
np.dot(np.array(Glist[i]), Vi[:, i + 1]))
taulist[i] = np.dot(np.array(Fi).T, Ai[:, i])
return taulist对于逆动力学算法而言,需要做的事情是:根据关节位置、速度、加速度计算关节力矩。
我们先看函数的输入:
thetalist:各关节角度
dthetalist:各关节速度
ddthetalist:各关节加速度
g:重力向量(向上为正方向)
Ftip:末端执行器作用于环境的力旋量。
Mlist:在初始零位时,i轴坐标系相对于i-1轴的变换(可以看到注释中提到,包括M01,M12,M23,M34,即第一轴并不在原点。这里的示例是一个三轴机器人,而零位矩阵M却出现了四组矩阵,M01代表第1轴到base的变换,M12代表2轴到1轴的变换,M23则是第三轴的,M34代表末端执行器到第三轴的变换。所以说0代表的是基坐标系)
Glist:连杆的空间惯量矩阵
Slist:Space系下各关节的螺旋轴,按列来排布
我们知道根据【现代机器人学】学习笔记七:开链动力学(前向动力学Forward dynamics 与逆动力学Inverse dynamics)
中提到的逆动力学方法,前向迭代+后向迭代:

首先,我们看到作者像是在写C++一样的初始化了一堆变量,因为他后面要在循环中赋值:
n = len(thetalist)
Mi = np.eye(4)
Ai = np.zeros((6, n))
AdTi = [[None]] * (n + 1)
Vi = np.zeros((6, n + 1))
Vdi = np.zeros((6, n + 1))
Vdi[:, 0] = np.r_[[0, 0, 0], -np.array(g)]
AdTi[n] = Adjoint(TransInv(Mlist[n]))
Fi = np.array(Ftip).copy()
taulist = np.zeros(n)1. 我们可以看到作者用Vi表示旋量,Vdi表示旋量的速度,并且通过 Vdi[:, 0] = np.r_[[0, 0, 0], -np.array(g)] 把第一列置为(0,0,0,0,0,-g),这里我们要注意,输入的g是(0,0,-9.8)那么在这里-g就是把-9.8变成了9.8。
2.我们可以看到,n为轴的数目,Vi,Vdi均设置为n+1大小。(并不是因为多了一个末端执行器,而是因为多了一个基坐标系,这点千万要注意,否则会被下标绕晕过去)。
而AdTi也是n+1大小,这里则是考虑了末端执行器,第一个数装从第一个轴和基坐标系的Ad转换,最后一个数装从末端执行器和第n轴的Ad转换。
而Ai为螺旋轴,就和机械臂轴的数目保持一致就好了。
3.定义一个Mi作为单位阵,用于后面保持连乘的格式。
Fi的初值为末端执行器的力旋量,也是用于后文反向迭代的连乘格式。
for i in range(n):
Mi = np.dot(Mi,Mlist[i])
Ai[:, i] = np.dot(Adjoint(TransInv(Mi)), np.array(Slist)[:, i])
AdTi[i] = Adjoint(np.dot(MatrixExp6(VecTose3(Ai[:, i] * \
-thetalist[i])), \
TransInv(Mlist[i])))
Vi[:, i + 1] = np.dot(AdTi[i], Vi[:,i]) + Ai[:, i] * dthetalist[i]
Vdi[:, i + 1] = np.dot(AdTi[i], Vdi[:, i]) \
+ Ai[:, i] * ddthetalist[i] \
+ np.dot(ad(Vi[:, i + 1]), Ai[:, i]) * dthetalist[i]我们观察一下前向迭代的过程:
循环为从1~n,即在代码中为for i in range(n),从0到n-1。因为代码是以0为下标的。
然后看前向迭代的第一步:

theta_i我们知道是第i轴的关节角,那么Ai是啥?
这个Ai,它直观意义是,关节i的初始螺旋轴在连杆坐标系i中的表示。
因此,我们需要先得到Mi:如何得到呢? Mi = np.dot(Mi,Mlist[i])。我们知道输入的Mlist中,依次为M01,M12...所以在前向迭代的过程中,每一轮搞一个连乘就好。
得到Mi,我们通过这一个步骤:
Ai[:, i] = np.dot(Adjoint(TransInv(Mi)), np.array(Slist)[:, i]),实现

所以在代码中Ai大小也为n,和螺旋轴一一对应。
那么现在元素齐全,就可以放心的得到i坐标系下,第i-1轴的表示了:

np.dot(MatrixExp6(VecTose3(Ai[:, i] * \
-thetalist[i])), \
TransInv(Mlist[i]))我们注意到,Mlist中存放的实际上是M(i,i+1),因此这里需要先求一个逆矩阵。
我们这里可以注意,对于边界条件,例如第一个数,代码中i=0的情况:我们最开始定义了一个Mi为单位矩阵,即用到了这里。对于M中的首个元素,M01,第一步可以成功求出一个T10,符合规范。0代表基坐标系,1代表第一轴。
然后计算前向迭代中的第二项:

第一个Ad,实现对旋量的坐标系转换,即直接调用以前实现的Adjoint函数就可以:
AdTi[i] = Adjoint(np.dot(MatrixExp6(VecTose3(Ai[:, i] * \
-thetalist[i])), \
TransInv(Mlist[i])))然后代码就简单了起来:
Vi[:, i + 1] = np.dot(AdTi[i], Vi[:,i]) + Ai[:, i] * dthetalist[i]照猫画虎,即:连杆i的运动旋量,由两部分构成:以i坐标系表示的i-1连杆的运动旋量,和i关节的速度引起的附加运动旋量构成。
这里注意下代码中的写法:因为其Vi使用的大小是i+1大小,也就是说,从i=1开始才是第0轴的旋量。
在第一轮迭代中,Ai[:, i] * dthetalist[i]是第1轴速度引起的附加运动旋量,
Vi[:,0]代表基坐标系的旋量,肯定默认为0。而AdTi[0]算出的则是T10的伴随矩阵。即以第一轴坐标系表示的基坐标系的运动旋量。
所以这段代码要注意:
Vi,Vdi均设置为n+1大小。(并不是因为多了一个末端执行器,而是因为多了一个基坐标系)。
V0代表基坐标系,V1代表第一轴,V2代表第二轴....
而AdTi也是n+1大小,这里则是考虑了末端执行器,即AdT0代表的是在1轴坐标系下基坐标系的运动旋量!
ok,搞明白了这个坐标关系,就i可以继续看旋量的速度了:

Vdi[:, i + 1] = np.dot(AdTi[i], Vdi[:, i]) \
+ Ai[:, i] * ddthetalist[i] \
+ np.dot(ad(Vi[:, i + 1]), Ai[:, i]) * dthetalist[i]加速度辅助记忆方法: 自身关节加速度
+ i系中连杆i-1加速度引起的分量
+ 速度李括号叉积分量 。
而速度叉积分量(两个旋量李括号)则是推导得到的,见中文版179页。
然后我们再看逆向迭代:
for i in range (n - 1, -1, -1):
Fi = np.dot(np.array(AdTi[i + 1]).T, Fi) \
+ np.dot(np.array(Glist[i]), Vdi[:, i + 1]) \
- np.dot(np.array(ad(Vi[:, i + 1])).T, \
np.dot(np.array(Glist[i]), Vi[:, i + 1]))
taulist[i] = np.dot(np.array(Fi).T, Ai[:, i])
return taulist这个对应公式:

我们注意看循环的下标,从n-1开始倒着推到-1。这是因为公式到处有i+1。
1.注意这个力旋量公式,我们可以这样来记忆它:
作用在连杆i上的总的力旋量,等于 “通过i+1施加在连杆上的力旋量” ,以及自身力旋量之和(包括一个旋量加速度的线性项,一个旋量的二次项)。
2. 对于这个公式,辅助记忆:执行器只要在关节旋量轴的方向提供标量力或力矩。因此得到力旋量,配合螺旋轴,就可以对应得到关节力矩。(记得转置)
那么总结一下,这个前向+后向的逻辑,就是通过前向迭代得到位姿、速度、加速度,逆向迭代则是把末端的力旋量一路反推回来,并换算为关节力矩或力。
MassMatrix:计算质量矩阵
def MassMatrix(thetalist, Mlist, Glist, Slist):
"""Computes the mass matrix of an open chain robot based on the given
configuration
:param thetalist: A list of joint variables
:param Mlist: List of link frames i relative to i-1 at the home position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:return: The numerical inertia matrix M(thetalist) of an n-joint serial
chain at the given configuration thetalist
This function calls InverseDynamics n times, each time passing a
ddthetalist vector with a single element equal to one and all other
inputs set to zero.
Each call of InverseDynamics generates a single column, and these columns
are assembled to create the inertia matrix.
Example Input (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
Output:
np.array([[ 2.25433380e+01, -3.07146754e-01, -7.18426391e-03]
[-3.07146754e-01, 1.96850717e+00, 4.32157368e-01]
[-7.18426391e-03, 4.32157368e-01, 1.91630858e-01]])
"""
n = len(thetalist)
M = np.zeros((n, n))
for i in range (n):
ddthetalist = [0] * n
ddthetalist[i] = 1
M[:, i] = InverseDynamics(thetalist, [0] * n, ddthetalist, \
[0, 0, 0], [0, 0, 0, 0, 0, 0], Mlist, \
Glist, Slist)
return M这个代码的做法看着好像很简单,就是每次迭代把速度、加速度全置为0,包括重力项也为0,然后仅把第i轴的加速度置为1。然后通过ID算法迭代得到关节力矩,塞到列中就是质量矩阵。
这个计算方法,见中文版183页。这也暗示了质量矩阵中各列的含义。
质量矩阵M其实在客观上起到一个从关节加速度到关节力矩互相之间的映射,
VelQuadraticForces:计算科里奥力项和向心项
def VelQuadraticForces(thetalist, dthetalist, Mlist, Glist, Slist):
"""Computes the Coriolis and centripetal terms in the inverse dynamics of
an open chain robot
:param thetalist: A list of joint variables,
:param dthetalist: A list of joint rates,
:param Mlist: List of link frames i relative to i-1 at the home position,
:param Glist: Spatial inertia matrices Gi of the links,
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns.
:return: The vector c(thetalist,dthetalist) of Coriolis and centripetal
terms for a given thetalist and dthetalist.
This function calls InverseDynamics with g = 0, Ftip = 0, and
ddthetalist = 0.
Example Input (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
Output:
np.array([0.26453118, -0.05505157, -0.00689132])
"""
return InverseDynamics(thetalist, dthetalist, [0] * len(thetalist), \
[0, 0, 0], [0, 0, 0, 0, 0, 0], Mlist, Glist, \
Slist)这点可以结合动力学这节课最开始的内容。当关节加速度都是0的时候,其包含了向心力与科里奥利力,因此关节角加速度为0的情况下,使得关节质心位置仍然存在一个加速度。(注意:此时的关节速度不是0!)
GravityForces:计算克服重力所需的关节力/力矩
def GravityForces(thetalist, g, Mlist, Glist, Slist):
"""Computes the joint forces/torques an open chain robot requires to
overcome gravity at its configuration
:param thetalist: A list of joint variables
:param g: 3-vector for gravitational acceleration
:param Mlist: List of link frames i relative to i-1 at the home position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:return grav: The joint forces/torques required to overcome gravity at
thetalist
This function calls InverseDynamics with Ftip = 0, dthetalist = 0, and
ddthetalist = 0.
Example Inputs (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
g = np.array([0, 0, -9.8])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
Output:
np.array([28.40331262, -37.64094817, -5.4415892])
"""
n = len(thetalist)
return InverseDynamics(thetalist, [0] * n, [0] * n, g, \
[0, 0, 0, 0, 0, 0], Mlist, Glist, Slist)这个写法则一目了然,此时机器人只受到重力项,其他关节位置、速度、加速度都是0,在当前位形下计算关节力矩即可。
EndEffectorForces:计算创建末端执行器力Ftip所需的关节力/扭矩
def EndEffectorForces(thetalist, Ftip, Mlist, Glist, Slist):
"""Computes the joint forces/torques an open chain robot requires only to
create the end-effector force Ftip
:param thetalist: A list of joint variables
:param Ftip: Spatial force applied by the end-effector expressed in frame
{n+1}
:param Mlist: List of link frames i relative to i-1 at the home position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:return: The joint forces and torques required only to create the
end-effector force Ftip
This function calls InverseDynamics with g = 0, dthetalist = 0, and
ddthetalist = 0.
Example Input (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
Ftip = np.array([1, 1, 1, 1, 1, 1])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
Output:
np.array([1.40954608, 1.85771497, 1.392409])
"""
n = len(thetalist)
return InverseDynamics(thetalist, [0] * n, [0] * n, [0, 0, 0], Ftip, \
Mlist, Glist, Slist)令速度、加速度为0,不受重力项,产生末端力旋量Ftip,调用逆动力学即可解算。
ForwardDynamics:前向动力学
def ForwardDynamics(thetalist, dthetalist, taulist, g, Ftip, Mlist, \
Glist, Slist):
"""Computes forward dynamics in the space frame for an open chain robot
:param thetalist: A list of joint variables
:param dthetalist: A list of joint rates
:param taulist: An n-vector of joint forces/torques
:param g: Gravity vector g
:param Ftip: Spatial force applied by the end-effector expressed in frame
{n+1}
:param Mlist: List of link frames i relative to i-1 at the home position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:return: The resulting joint accelerations
This function computes ddthetalist by solving:
Mlist(thetalist) * ddthetalist = taulist - c(thetalist,dthetalist) \
- g(thetalist) - Jtr(thetalist) * Ftip
Example Input (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
taulist = np.array([0.5, 0.6, 0.7])
g = np.array([0, 0, -9.8])
Ftip = np.array([1, 1, 1, 1, 1, 1])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
Output:
np.array([-0.97392907, 25.58466784, -32.91499212])
"""
return np.dot(np.linalg.inv(MassMatrix(thetalist, Mlist, Glist, \
Slist)), \
np.array(taulist) \
- VelQuadraticForces(thetalist, dthetalist, Mlist, \
Glist, Slist) \
- GravityForces(thetalist, g, Mlist, Glist, Slist) \
- EndEffectorForces(thetalist, Ftip, Mlist, Glist, \
Slist))
前向运动学的做法是,输入关节位置、速度、末端力,扭矩等信息,计算关节加速度。
所以我们的做法是,先计算质量矩阵,然后把上式的M通过逆矩阵乘到等式右侧。
那么等式右侧是,扭矩 - 科氏力和向心力 - 重力项 - 末端力。即加速度要起到这么多作用。(h其实是向心力、科氏力,重力,摩擦力等各种力集合在一起的向量)
当然我们观察到有一点区别:
公式中末端力旋量左乘了雅可比的转置,这个其实是参照了第五章速度运动学和静力学的知识:
【现代机器人学】学习笔记四:一阶运动学与静力学

即为提供这样的力旋量,关节需要提供这样的扭矩。
但我们的代码中,并没有这样计算,而是直接调用前面写好的函数EndEffectorForces:计算创建末端执行器力Ftip所需的关节力/扭矩, 然后得到机器人需要支持末端力的关节扭矩。
逆动力学算法可用于计算(总结一下):
| 计算内容 |
关节位置 | 关节速度 | 关节加速度 | 末端力旋量 | 重力项 | 如何计算 |
| 质量矩阵 | 需要 | 均为0 | 依次将第i轴加速度置为1,其他轴为0。 | 0 | 0 | 调用逆动力学,计算ID,将ID结果填充质量矩阵的第i列 |
| 提供科氏力和向心力的力矩 | 需要 | 需要 | 均为0 | 0 | 0 | 直接根据所述配置计算ID |
| 提供重力项的力矩 | 需要 | 均为0 | 均为0 | 0 | 需要,g | 直接根据所述配置计算ID |
| 提供提供末端力的力矩 | 需要 | 均为0 | 均为0 | 需要,Ftip | 0 | 直接根据所述配置计算ID |
EulerStep:欧拉积分工具函数
def EulerStep(thetalist, dthetalist, ddthetalist, dt):
"""Compute the joint angles and velocities at the next timestep using from here
first order Euler integration
:param thetalist: n-vector of joint variables
:param dthetalist: n-vector of joint rates
:param ddthetalist: n-vector of joint accelerations
:param dt: The timestep delta t
:return thetalistNext: Vector of joint variables after dt from first
order Euler integration
:return dthetalistNext: Vector of joint rates after dt from first order
Euler integration
Example Inputs (3 Link Robot):
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
ddthetalist = np.array([2, 1.5, 1])
dt = 0.1
Output:
thetalistNext:
array([ 0.11, 0.12, 0.13])
dthetalistNext:
array([ 0.3 , 0.35, 0.4 ])
"""
return thetalist + dt * np.array(dthetalist), \
dthetalist + dt * np.array(ddthetalist)这个函数是一个工具函数,主要被用在 正向动力学的欧拉积分算法 部分。
输入是关节角度,关节速度,关节加速度,以及用于积分的周期。

InverseDynamicsTrajectory :给定轨迹,计算轨迹中各时刻的关节力矩
def InverseDynamicsTrajectory(thetamat, dthetamat, ddthetamat, g, \
Ftipmat, Mlist, Glist, Slist):
"""Calculates the joint forces/torques required to move the serial chain
along the given trajectory using inverse dynamics
:param thetamat: An N x n matrix of robot joint variables
:param dthetamat: An N x n matrix of robot joint velocities
:param ddthetamat: An N x n matrix of robot joint accelerations
:param g: Gravity vector g
:param Ftipmat: An N x 6 matrix of spatial forces applied by the end-
effector (If there are no tip forces the user should
input a zero and a zero matrix will be used)
:param Mlist: List of link frames i relative to i-1 at the home position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:return: The N x n matrix of joint forces/torques for the specified
trajectory, where each of the N rows is the vector of joint
forces/torques at each time step
Example Inputs (3 Link Robot):
from __future__ import print_function
import numpy as np
import modern_robotics as mr
# Create a trajectory to follow using functions from Chapter 9
thetastart = np.array([0, 0, 0])
thetaend = np.array([np.pi / 2, np.pi / 2, np.pi / 2])
Tf = 3
N= 1000
method = 5
traj = mr.JointTrajectory(thetastart, thetaend, Tf, N, method)
thetamat = np.array(traj).copy()
dthetamat = np.zeros((1000,3 ))
ddthetamat = np.zeros((1000, 3))
dt = Tf / (N - 1.0)
for i in range(np.array(traj).shape[0] - 1):
dthetamat[i + 1, :] = (thetamat[i + 1, :] - thetamat[i, :]) / dt
ddthetamat[i + 1, :] \
= (dthetamat[i + 1, :] - dthetamat[i, :]) / dt
# Initialize robot description (Example with 3 links)
g = np.array([0, 0, -9.8])
Ftipmat = np.ones((N, 6))
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
taumat \
= mr.InverseDynamicsTrajectory(thetamat, dthetamat, ddthetamat, g, \
Ftipmat, Mlist, Glist, Slist)
# Output using matplotlib to plot the joint forces/torques
Tau1 = taumat[:, 0]
Tau2 = taumat[:, 1]
Tau3 = taumat[:, 2]
timestamp = np.linspace(0, Tf, N)
try:
import matplotlib.pyplot as plt
except:
print('The result will not be plotted due to a lack of package matplotlib')
else:
plt.plot(timestamp, Tau1, label = "Tau1")
plt.plot(timestamp, Tau2, label = "Tau2")
plt.plot(timestamp, Tau3, label = "Tau3")
plt.ylim (-40, 120)
plt.legend(loc = 'lower right')
plt.xlabel("Time")
plt.ylabel("Torque")
plt.title("Plot of Torque Trajectories")
plt.show()
"""
thetamat = np.array(thetamat).T
dthetamat = np.array(dthetamat).T
ddthetamat = np.array(ddthetamat).T
Ftipmat = np.array(Ftipmat).T
taumat = np.array(thetamat).copy()
for i in range(np.array(thetamat).shape[1]):
taumat[:, i] \
= InverseDynamics(thetamat[:, i], dthetamat[:, i], \
ddthetamat[:, i], g, Ftipmat[:, i], Mlist, \
Glist, Slist)
taumat = np.array(taumat).T
return taumat前面我们介绍的,都是某一个时刻的关节力矩,那我们如果控制的比较底层,例如我们只能控制关节力矩,如何才能忠实的执行某一条轨迹呢?那这则比较简单,只需要调用我们前面的逆动力学算法就可以了。
回顾在InverseDynamics函数中的各个参数:
thetalist:各关节角度
dthetalist:各关节速度
ddthetalist:各关节加速度
g:重力向量(向上为正方向)
Ftip:末端执行器作用于环境的力旋量。
Mlist:在初始零位时,i轴坐标系相对于i-1轴的变换(可以看到注释中提到,包括M01,M12,M23,M34,即第一轴并不在原点。这里的示例是一个三轴机器人,而零位矩阵M却出现了四组矩阵,M01代表第1轴到base的变换,M12代表2轴到1轴的变换,M23则是第三轴的,M34代表末端执行器到第三轴的变换。所以说0代表的是基坐标系)
Glist:连杆的空间惯量矩阵
Slist:Space系下各关节的螺旋轴,按列来排布
那么在代码中,我们只要将每个时刻的上述参数传入逆动力学函数当中,即可求解各个时刻的关节力矩。
注意在注释中提到,返回值是一个N*n的矩阵,其中N代表时间戳,因此将计算出的矩阵转置再进行返回。
ForwardDynamicsTrajectory:给定关节力矩序列,推算机械臂运动
def ForwardDynamicsTrajectory(thetalist, dthetalist, taumat, g, Ftipmat, \
Mlist, Glist, Slist, dt, intRes):
"""Simulates the motion of a serial chain given an open-loop history of
joint forces/torques
:param thetalist: n-vector of initial joint variables
:param dthetalist: n-vector of initial joint rates
:param taumat: An N x n matrix of joint forces/torques, where each row is
the joint effort at any time step
:param g: Gravity vector g
:param Ftipmat: An N x 6 matrix of spatial forces applied by the end-
effector (If there are no tip forces the user should
input a zero and a zero matrix will be used)
:param Mlist: List of link frames {i} relative to {i-1} at the home
position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:param dt: The timestep between consecutive joint forces/torques
:param intRes: Integration resolution is the number of times integration
(Euler) takes places between each time step. Must be an
integer value greater than or equal to 1
:return thetamat: The N x n matrix of robot joint angles resulting from
the specified joint forces/torques
:return dthetamat: The N x n matrix of robot joint velocities
This function calls a numerical integration procedure that uses
ForwardDynamics.
Example Inputs (3 Link Robot):
from __future__ import print_function
import numpy as np
import modern_robotics as mr
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
taumat = np.array([[3.63, -6.58, -5.57], [3.74, -5.55, -5.5],
[4.31, -0.68, -5.19], [5.18, 5.63, -4.31],
[5.85, 8.17, -2.59], [5.78, 2.79, -1.7],
[4.99, -5.3, -1.19], [4.08, -9.41, 0.07],
[3.56, -10.1, 0.97], [3.49, -9.41, 1.23]])
# Initialize robot description (Example with 3 links)
g = np.array([0, 0, -9.8])
Ftipmat = np.ones((np.array(taumat).shape[0], 6))
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
dt = 0.1
intRes = 8
thetamat,dthetamat \
= mr.ForwardDynamicsTrajectory(thetalist, dthetalist, taumat, g, \
Ftipmat, Mlist, Glist, Slist, dt, \
intRes)
# Output using matplotlib to plot the joint angle/velocities
theta1 = thetamat[:, 0]
theta2 = thetamat[:, 1]
theta3 = thetamat[:, 2]
dtheta1 = dthetamat[:, 0]
dtheta2 = dthetamat[:, 1]
dtheta3 = dthetamat[:, 2]
N = np.array(taumat).shape[0]
Tf = np.array(taumat).shape[0] * dt
timestamp = np.linspace(0, Tf, N)
try:
import matplotlib.pyplot as plt
except:
print('The result will not be plotted due to a lack of package matplotlib')
else:
plt.plot(timestamp, theta1, label = "Theta1")
plt.plot(timestamp, theta2, label = "Theta2")
plt.plot(timestamp, theta3, label = "Theta3")
plt.plot(timestamp, dtheta1, label = "DTheta1")
plt.plot(timestamp, dtheta2, label = "DTheta2")
plt.plot(timestamp, dtheta3, label = "DTheta3")
plt.ylim (-12, 10)
plt.legend(loc = 'lower right')
plt.xlabel("Time")
plt.ylabel("Joint Angles/Velocities")
plt.title("Plot of Joint Angles and Joint Velocities")
plt.show()
"""
taumat = np.array(taumat).T
Ftipmat = np.array(Ftipmat).T
thetamat = taumat.copy().astype(float)
thetamat[:, 0] = thetalist
dthetamat = taumat.copy().astype(float)
dthetamat[:, 0] = dthetalist
for i in range(np.array(taumat).shape[1] - 1):
for j in range(intRes):
ddthetalist \
= ForwardDynamics(thetalist, dthetalist, taumat[:, i], g, \
Ftipmat[:, i], Mlist, Glist, Slist)
thetalist,dthetalist = EulerStep(thetalist, dthetalist, \
ddthetalist, 1.0 * dt / intRes)
thetamat[:, i + 1] = thetalist
dthetamat[:, i + 1] = dthetalist
thetamat = np.array(thetamat).T
dthetamat = np.array(dthetamat).T
return thetamat, dthetamat相信看到这里的同学内心可能会觉得可以快进了,认为这个函数并没有想象的复杂。
但是,千万不能麻痹大意!!
因为我们观察到新出现了一个参数:intRes。这个参数意味着的意思是,积分步的数目。要求这个数字是大于等于1的整数。
另外函数的形参还有:初始的关节角度、速度。
我们有一点需要明确注意:
细看代码,我们可以看到:ForwardDynamics这个函数出现在了i,j的两轮循环内部。
ForwardDynamics(thetalist, dthetalist, taumat[:, i], g, \
Ftipmat[:, i], Mlist, Glist, Slist)但是我们似乎发现,代码中并没有用到变量j,但这并不意味着ForwardDynamics可以放到j的外层,即i这层循环中。
为什么呢?
我们有的是初始的角度、速度,以及N个时刻的关节力矩。我们可以发现,在迭代的过程中,关节位置、速度和力矩处于一种耦合的关系。
诚然,我们可以根据初始时刻的力矩,然后以此力矩算出初始时刻的加速度,保持此加速度,然后推算第二帧力矩时刻的位置、速度、加速度;
但是我们不要忘了,在第i帧到第i+1帧的过程中,机械臂的位置、速度、加速度并不是恒定不变的!
也就是说,在输入的力矩的第i帧到第i+1帧的过程中,位置、速度等等稍微动一动,根据前向动力学算出的加速度就变了,因为机械臂是一个现实中的物体,它的变化肯定不是离散一格一格变化的,以至于这是一个连续的过程。因此这里才引入了intRes这个参数,即内层循环j。我们通过intRes参数,把时间步长划分的足够小,假设从第i帧到第i+1帧花费delta_t时间,这样就可以把中间拆分出intRes段,每段时长是delta_t/intRes,这样就把原先delta_t时间段内加速度不变的假设,转换成了delta_t/intRes时间段内加速度不变的假设,大大提高了计算的精准度。
如书中所述,也符合我们实际的感觉,当intRes这个积分步数无限大,则数值积分的结果趋近于理论结果。
读到这里,可能朋友们有一个疑问:那为啥上一个函数,InverseDynamicsTrajectory ,它就不需要搞两层循环这样做?
啊,这个原因是因为InverseDynamicsTrajectory中的形参就是各个控制周期时刻的位置、速度、加速度,我们根据这些变量就能用逆动力学精准的算出对应时刻的关节力矩。
而在现在的这个函数中,我们仅仅给定关节力矩的序列,此时并没有位置、速度的信息,这些信息要靠递推才能得到。但递推的精准度则需要靠各个时刻精准的加速度来推算,加速度是变化的因此只能用离散的积分来代替。
机器人轨迹生成部分:
CubicTimeScaling:三次多项式缩放时间尺度
def CubicTimeScaling(Tf, t):
"""Computes s(t) for a cubic time scaling
:param Tf: Total time of the motion in seconds from rest to rest
:param t: The current time t satisfying 0 < t < Tf
:return: The path parameter s(t) corresponding to a third-order
polynomial motion that begins and ends at zero velocity
Example Input:
Tf = 2
t = 0.6
Output:
0.216
"""
return 3 * (1.0 * t / Tf) ** 2 - 2 * (1.0 * t / Tf) ** 3输入周期,以及当前时间,然后对时间进行缩放,使其满足三次多项式,起点和终点以0速度开始和结束。
QuinticTimeScaling:五次多项式缩放时间尺度
def QuinticTimeScaling(Tf, t):
"""Computes s(t) for a quintic time scaling
:param Tf: Total time of the motion in seconds from rest to rest
:param t: The current time t satisfying 0 < t < Tf
:return: The path parameter s(t) corresponding to a fifth-order
polynomial motion that begins and ends at zero velocity and zero
acceleration
Example Input:
Tf = 2
t = 0.6
Output:
0.16308
"""
return 10 * (1.0 * t / Tf) ** 3 - 15 * (1.0 * t / Tf) ** 4 \
+ 6 * (1.0 * t / Tf) ** 5输入周期,以及当前时间,对时间进行缩放,使其满足五次多项式,起点和终点以0速度和0加速度开始和结束。
如何计算三次/五次多项式的系数?
这点我们可以参见博文:
【现代机器人学】学习笔记八:轨迹生成
我们使用sympy:
import sympy as sym
import numpy as np
T = sym.symbols('T')
a=sym.symarray('a', 6)
b=sym.Matrix([0,0,0,1,0,0])
poly_T=sym.Matrix([[1,0,0,0,0,0], [0,1,0,0,0,0], [0,0,2,0,0,0], [1,T,T**2,T**3,T**4,T**5], [0,1,2*T,3*T**2,4*T**3,5*T**4], [0,0,2,6*T,12*T**2,20*T**3]])
inv_poly_T=poly_T.inv()
result=inv_poly_T*b
print(result)
————————————————
版权声明:本文为CSDN博主「zkk9527」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/zkk9527/article/details/128487742
对于不同的位置、速度、加速度要求,我们修改b即可。
JointTrajectory:关节空间轨迹平滑插值
def JointTrajectory(thetastart, thetaend, Tf, N, method):
"""Computes a straight-line trajectory in joint space
:param thetastart: The initial joint variables
:param thetaend: The final joint variables
:param Tf: Total time of the motion in seconds from rest to rest
:param N: The number of points N > 1 (Start and stop) in the discrete
representation of the trajectory
:param method: The time-scaling method, where 3 indicates cubic (third-
order polynomial) time scaling and 5 indicates quintic
(fifth-order polynomial) time scaling
:return: A trajectory as an N x n matrix, where each row is an n-vector
of joint variables at an instant in time. The first row is
thetastart and the Nth row is thetaend . The elapsed time
between each row is Tf / (N - 1)
Example Input:
thetastart = np.array([1, 0, 0, 1, 1, 0.2, 0,1])
thetaend = np.array([1.2, 0.5, 0.6, 1.1, 2, 2, 0.9, 1])
Tf = 4
N = 6
method = 3
Output:
np.array([[ 1, 0, 0, 1, 1, 0.2, 0, 1]
[1.0208, 0.052, 0.0624, 1.0104, 1.104, 0.3872, 0.0936, 1]
[1.0704, 0.176, 0.2112, 1.0352, 1.352, 0.8336, 0.3168, 1]
[1.1296, 0.324, 0.3888, 1.0648, 1.648, 1.3664, 0.5832, 1]
[1.1792, 0.448, 0.5376, 1.0896, 1.896, 1.8128, 0.8064, 1]
[ 1.2, 0.5, 0.6, 1.1, 2, 2, 0.9, 1]])
"""
N = int(N)
timegap = Tf / (N - 1.0)
traj = np.zeros((len(thetastart), N))
for i in range(N):
if method == 3:
s = CubicTimeScaling(Tf, timegap * i)
else:
s = QuinticTimeScaling(Tf, timegap * i)
traj[:, i] = s * np.array(thetaend) + (1 - s) * np.array(thetastart)
traj = np.array(traj).T
return traj我们想在关节空间走一条直线,那我们如何做呢?利用刚刚得到的三次或者五次的时间尺度缩放函数,等间断的送入当前时长,返回一个系数s,然后实现s*终点 + (1-s)*起点。由于s会从0缓慢的运动到1,因此也第i个时刻算出的结果也会从起点平滑的过渡到终点。
当然,我们也可以不这样做,直接对起点和终点的坐标做三次/五次多项式直接平滑轨迹,也并无不可。
ScrewTrajectory:螺旋轴空间平滑插值
def ScrewTrajectory(Xstart, Xend, Tf, N, method):
"""Computes a trajectory as a list of N SE(3) matrices corresponding to
the screw motion about a space screw axis
:param Xstart: The initial end-effector configuration
:param Xend: The final end-effector configuration
:param Tf: Total time of the motion in seconds from rest to rest
:param N: The number of points N > 1 (Start and stop) in the discrete
representation of the trajectory
:param method: The time-scaling method, where 3 indicates cubic (third-
order polynomial) time scaling and 5 indicates quintic
(fifth-order polynomial) time scaling
:return: The discretized trajectory as a list of N matrices in SE(3)
separated in time by Tf/(N-1). The first in the list is Xstart
and the Nth is Xend
Example Input:
Xstart = np.array([[1, 0, 0, 1],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]])
Xend = np.array([[0, 0, 1, 0.1],
[1, 0, 0, 0],
[0, 1, 0, 4.1],
[0, 0, 0, 1]])
Tf = 5
N = 4
method = 3
Output:
[np.array([[1, 0, 0, 1]
[0, 1, 0, 0]
[0, 0, 1, 1]
[0, 0, 0, 1]]),
np.array([[0.904, -0.25, 0.346, 0.441]
[0.346, 0.904, -0.25, 0.529]
[-0.25, 0.346, 0.904, 1.601]
[ 0, 0, 0, 1]]),
np.array([[0.346, -0.25, 0.904, -0.117]
[0.904, 0.346, -0.25, 0.473]
[-0.25, 0.904, 0.346, 3.274]
[ 0, 0, 0, 1]]),
np.array([[0, 0, 1, 0.1]
[1, 0, 0, 0]
[0, 1, 0, 4.1]
[0, 0, 0, 1]])]
"""
N = int(N)
timegap = Tf / (N - 1.0)
traj = [[None]] * N
for i in range(N):
if method == 3:
s = CubicTimeScaling(Tf, timegap * i)
else:
s = QuinticTimeScaling(Tf, timegap * i)
traj[i] \
= np.dot(Xstart, MatrixExp6(MatrixLog6(np.dot(TransInv(Xstart), \
Xend)) * s))
return traj关于这个函数,输入的是起点和终点的位姿,总时长,分段数,以及三次/五次方法。
代码的写法开始是一样的,算出一个s来。那么这个s是从0平滑的运动到1。
接下来就看怎么操作:
Xstart意味着Tbs,Xend意味着Tbe,对Tbs快捷求逆,即Tsb,乘以Tbe得到Tse,即从start到end的相对的齐次变换:np.dot(TransInv(Xstart), Xend)
然后我们调用对数公式,把这各齐次矩阵给它变成se3(其中包含角度的theta项,请回顾上文)
然后把这个螺旋轴乘以从0平滑的过渡到1的系数,然后再用指数公式给它变回去,作用到原先的Xstart上,起到在旋量空间平滑插值的作用。
CartesianTrajectory:笛卡尔空间平滑插值
def CartesianTrajectory(Xstart, Xend, Tf, N, method):
"""Computes a trajectory as a list of N SE(3) matrices corresponding to
the origin of the end-effector frame following a straight line
:param Xstart: The initial end-effector configuration
:param Xend: The final end-effector configuration
:param Tf: Total time of the motion in seconds from rest to rest
:param N: The number of points N > 1 (Start and stop) in the discrete
representation of the trajectory
:param method: The time-scaling method, where 3 indicates cubic (third-
order polynomial) time scaling and 5 indicates quintic
(fifth-order polynomial) time scaling
:return: The discretized trajectory as a list of N matrices in SE(3)
separated in time by Tf/(N-1). The first in the list is Xstart
and the Nth is Xend
This function is similar to ScrewTrajectory, except the origin of the
end-effector frame follows a straight line, decoupled from the rotational
motion.
Example Input:
Xstart = np.array([[1, 0, 0, 1],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]])
Xend = np.array([[0, 0, 1, 0.1],
[1, 0, 0, 0],
[0, 1, 0, 4.1],
[0, 0, 0, 1]])
Tf = 5
N = 4
method = 5
Output:
[np.array([[1, 0, 0, 1]
[0, 1, 0, 0]
[0, 0, 1, 1]
[0, 0, 0, 1]]),
np.array([[ 0.937, -0.214, 0.277, 0.811]
[ 0.277, 0.937, -0.214, 0]
[-0.214, 0.277, 0.937, 1.651]
[ 0, 0, 0, 1]]),
np.array([[ 0.277, -0.214, 0.937, 0.289]
[ 0.937, 0.277, -0.214, 0]
[-0.214, 0.937, 0.277, 3.449]
[ 0, 0, 0, 1]]),
np.array([[0, 0, 1, 0.1]
[1, 0, 0, 0]
[0, 1, 0, 4.1]
[0, 0, 0, 1]])]
"""
N = int(N)
timegap = Tf / (N - 1.0)
traj = [[None]] * N
Rstart, pstart = TransToRp(Xstart)
Rend, pend = TransToRp(Xend)
for i in range(N):
if method == 3:
s = CubicTimeScaling(Tf, timegap * i)
else:
s = QuinticTimeScaling(Tf, timegap * i)
traj[i] \
= np.r_[np.c_[np.dot(Rstart, \
MatrixExp3(MatrixLog3(np.dot(np.array(Rstart).T,Rend)) * s)), \
s * np.array(pend) + (1 - s) * np.array(pstart)], \
[[0, 0, 0, 1]]]
return traj这个函数属实不用怎么介绍了,就是把旋转和平移分开,旋转用so3来插值,位置用直线来插值,最后再拼到一起去。
机器人控制部分:
ComputedTorque:计算特定时刻的关节控制力矩
def ComputedTorque(thetalist, dthetalist, eint, g, Mlist, Glist, Slist, \
thetalistd, dthetalistd, ddthetalistd, Kp, Ki, Kd):
"""Computes the joint control torques at a particular time instant
:param thetalist: n-vector of joint variables
:param dthetalist: n-vector of joint rates
:param eint: n-vector of the time-integral of joint errors
:param g: Gravity vector g
:param Mlist: List of link frames {i} relative to {i-1} at the home
position
:param Glist: Spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:param thetalistd: n-vector of reference joint variables
:param dthetalistd: n-vector of reference joint velocities
:param ddthetalistd: n-vector of reference joint accelerations
:param Kp: The feedback proportional gain (identical for each joint)
:param Ki: The feedback integral gain (identical for each joint)
:param Kd: The feedback derivative gain (identical for each joint)
:return: The vector of joint forces/torques computed by the feedback
linearizing controller at the current instant
Example Input:
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
eint = np.array([0.2, 0.2, 0.2])
g = np.array([0, 0, -9.8])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
thetalistd = np.array([1.0, 1.0, 1.0])
dthetalistd = np.array([2, 1.2, 2])
ddthetalistd = np.array([0.1, 0.1, 0.1])
Kp = 1.3
Ki = 1.2
Kd = 1.1
Output:
np.array([133.00525246, -29.94223324, -3.03276856])
"""
e = np.subtract(thetalistd, thetalist)
return np.dot(MassMatrix(thetalist, Mlist, Glist, Slist), \
Kp * e + Ki * (np.array(eint) + e) \
+ Kd * np.subtract(dthetalistd, dthetalist)) \
+ InverseDynamics(thetalist, dthetalist, ddthetalistd, g, \
[0, 0, 0, 0, 0, 0], Mlist, Glist, Slist)我们可以看到这个函数的形参有一大堆,慢慢来分析一下:
:param thetalist: n维关节角度
:param dthetalist: n维关节速度
:param eint: 关节误差的积分项,这是因为pid控制中需要用到之前的积分
:param g: 重力向量
:param Mlist: i-1系下第i轴的位姿(零位时刻)
:param Glist: 空间惯量矩阵
:param Slist: Space系下的各个螺旋轴
:param thetalistd: n维期望的关节位置
:param dthetalistd: n维期望的关节速度
:param ddthetalistd:n维期望的关节加速度
:param Kp: PID控制中的Kp项
:param Ki: PID控制中的Ki项
:param Kd: PID控制中的Kd项
:return: 根据反馈控制,得到此瞬间的关节力矩
我们可以看到,首先用到了np的subtract函数,实际上就是相减函数,我们平时直接用减号,手动的写出subtract的反而比较少。
在调用subtract以后,得到了此时的关节误差,我们正常计算PID:
Kp * e + Ki * (np.array(eint) + e) + Kd * np.subtract(dthetalistd, dthetalist)
我们在得到了这个误差以后,下一步我们对它乘以了一个质量矩阵,并且加上了逆动力学算出的力矩。逆动力学算出的结果意味着:

把误差结合即可算出正常的前馈+反馈控制的结果:

这块可以结合
【现代机器人学】学习笔记十:机器人控制
进行复习。
SimulateControl:模拟力矩控制器去跟随一条期望的机器人轨迹
def SimulateControl(thetalist, dthetalist, g, Ftipmat, Mlist, Glist, \
Slist, thetamatd, dthetamatd, ddthetamatd, gtilde, \
Mtildelist, Gtildelist, Kp, Ki, Kd, dt, intRes):
"""Simulates the computed torque controller over a given desired
trajectory
:param thetalist: n-vector of initial joint variables
:param dthetalist: n-vector of initial joint velocities
:param g: Actual gravity vector g
:param Ftipmat: An N x 6 matrix of spatial forces applied by the end-
effector (If there are no tip forces the user should
input a zero and a zero matrix will be used)
:param Mlist: Actual list of link frames i relative to i-1 at the home
position
:param Glist: Actual spatial inertia matrices Gi of the links
:param Slist: Screw axes Si of the joints in a space frame, in the format
of a matrix with axes as the columns
:param thetamatd: An Nxn matrix of desired joint variables from the
reference trajectory
:param dthetamatd: An Nxn matrix of desired joint velocities
:param ddthetamatd: An Nxn matrix of desired joint accelerations
:param gtilde: The gravity vector based on the model of the actual robot
(actual values given above)
:param Mtildelist: The link frame locations based on the model of the
actual robot (actual values given above)
:param Gtildelist: The link spatial inertias based on the model of the
actual robot (actual values given above)
:param Kp: The feedback proportional gain (identical for each joint)
:param Ki: The feedback integral gain (identical for each joint)
:param Kd: The feedback derivative gain (identical for each joint)
:param dt: The timestep between points on the reference trajectory
:param intRes: Integration resolution is the number of times integration
(Euler) takes places between each time step. Must be an
integer value greater than or equal to 1
:return taumat: An Nxn matrix of the controllers commanded joint forces/
torques, where each row of n forces/torques corresponds
to a single time instant
:return thetamat: An Nxn matrix of actual joint angles
The end of this function plots all the actual and desired joint angles
using matplotlib and random libraries.
Example Input:
from __future__ import print_function
import numpy as np
from modern_robotics import JointTrajectory
thetalist = np.array([0.1, 0.1, 0.1])
dthetalist = np.array([0.1, 0.2, 0.3])
# Initialize robot description (Example with 3 links)
g = np.array([0, 0, -9.8])
M01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.089159],
[0, 0, 0, 1]])
M12 = np.array([[ 0, 0, 1, 0.28],
[ 0, 1, 0, 0.13585],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
M23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.1197],
[0, 0, 1, 0.395],
[0, 0, 0, 1]])
M34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.14225],
[0, 0, 0, 1]])
G1 = np.diag([0.010267, 0.010267, 0.00666, 3.7, 3.7, 3.7])
G2 = np.diag([0.22689, 0.22689, 0.0151074, 8.393, 8.393, 8.393])
G3 = np.diag([0.0494433, 0.0494433, 0.004095, 2.275, 2.275, 2.275])
Glist = np.array([G1, G2, G3])
Mlist = np.array([M01, M12, M23, M34])
Slist = np.array([[1, 0, 1, 0, 1, 0],
[0, 1, 0, -0.089, 0, 0],
[0, 1, 0, -0.089, 0, 0.425]]).T
dt = 0.01
# Create a trajectory to follow
thetaend = np.array([np.pi / 2, np.pi, 1.5 * np.pi])
Tf = 1
N = int(1.0 * Tf / dt)
method = 5
traj = mr.JointTrajectory(thetalist, thetaend, Tf, N, method)
thetamatd = np.array(traj).copy()
dthetamatd = np.zeros((N, 3))
ddthetamatd = np.zeros((N, 3))
dt = Tf / (N - 1.0)
for i in range(np.array(traj).shape[0] - 1):
dthetamatd[i + 1, :] \
= (thetamatd[i + 1, :] - thetamatd[i, :]) / dt
ddthetamatd[i + 1, :] \
= (dthetamatd[i + 1, :] - dthetamatd[i, :]) / dt
# Possibly wrong robot description (Example with 3 links)
gtilde = np.array([0.8, 0.2, -8.8])
Mhat01 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.1],
[0, 0, 0, 1]])
Mhat12 = np.array([[ 0, 0, 1, 0.3],
[ 0, 1, 0, 0.2],
[-1, 0, 0, 0],
[ 0, 0, 0, 1]])
Mhat23 = np.array([[1, 0, 0, 0],
[0, 1, 0, -0.2],
[0, 0, 1, 0.4],
[0, 0, 0, 1]])
Mhat34 = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0.2],
[0, 0, 0, 1]])
Ghat1 = np.diag([0.1, 0.1, 0.1, 4, 4, 4])
Ghat2 = np.diag([0.3, 0.3, 0.1, 9, 9, 9])
Ghat3 = np.diag([0.1, 0.1, 0.1, 3, 3, 3])
Gtildelist = np.array([Ghat1, Ghat2, Ghat3])
Mtildelist = np.array([Mhat01, Mhat12, Mhat23, Mhat34])
Ftipmat = np.ones((np.array(traj).shape[0], 6))
Kp = 20
Ki = 10
Kd = 18
intRes = 8
taumat,thetamat \
= mr.SimulateControl(thetalist, dthetalist, g, Ftipmat, Mlist, \
Glist, Slist, thetamatd, dthetamatd, \
ddthetamatd, gtilde, Mtildelist, Gtildelist, \
Kp, Ki, Kd, dt, intRes)
"""
Ftipmat = np.array(Ftipmat).T
thetamatd = np.array(thetamatd).T
dthetamatd = np.array(dthetamatd).T
ddthetamatd = np.array(ddthetamatd).T
m,n = np.array(thetamatd).shape
thetacurrent = np.array(thetalist).copy()
dthetacurrent = np.array(dthetalist).copy()
eint = np.zeros((m,1)).reshape(m,)
taumat = np.zeros(np.array(thetamatd).shape)
thetamat = np.zeros(np.array(thetamatd).shape)
for i in range(n):
taulist \
= ComputedTorque(thetacurrent, dthetacurrent, eint, gtilde, \
Mtildelist, Gtildelist, Slist, thetamatd[:, i], \
dthetamatd[:, i], ddthetamatd[:, i], Kp, Ki, Kd)
for j in range(intRes):
ddthetalist \
= ForwardDynamics(thetacurrent, dthetacurrent, taulist, g, \
Ftipmat[:, i], Mlist, Glist, Slist)
thetacurrent, dthetacurrent \
= EulerStep(thetacurrent, dthetacurrent, ddthetalist, \
1.0 * dt / intRes)
taumat[:, i] = taulist
thetamat[:, i] = thetacurrent
eint = np.add(eint, dt * np.subtract(thetamatd[:, i], thetacurrent))
# Output using matplotlib to plot
try:
import matplotlib.pyplot as plt
except:
print('The result will not be plotted due to a lack of package matplotlib')
else:
links = np.array(thetamat).shape[0]
N = np.array(thetamat).shape[1]
Tf = N * dt
timestamp = np.linspace(0, Tf, N)
for i in range(links):
col = [np.random.uniform(0, 1), np.random.uniform(0, 1),
np.random.uniform(0, 1)]
plt.plot(timestamp, thetamat[i, :], "-", color=col, \
label = ("ActualTheta" + str(i + 1)))
plt.plot(timestamp, thetamatd[i, :], ".", color=col, \
label = ("DesiredTheta" + str(i + 1)))
plt.legend(loc = 'upper left')
plt.xlabel("Time")
plt.ylabel("Joint Angles")
plt.title("Plot of Actual and Desired Joint Angles")
plt.show()
taumat = np.array(taumat).T
thetamat = np.array(thetamat).T
return (taumat, thetamat)
这是本文的最后一个函数了。我相信一路走到现在,对机器人的运动学、动力学已经算是比较熟悉的了,看懂这最后一个函数也不是什么困难。
那我们在这里细致的分析一下函数的输入:
:param thetalist: n维初始关节位置
:param dthetalist: n维初始关节速度
:param g: 实际的重力向量
:param Ftipmat: N* 6 大小的末端力旋量矩阵
:param Mlist: 实际的零位的i-1系中i系的位姿(位置矩阵)
:param Glist: 实际的空间惯量矩阵
:param Slist: 零位的螺旋轴向量
:param thetamatd: N*n大小的期望的关节位置轨迹
:param dthetamatd: N*n大小的期望关节速度轨迹
:param ddthetamatd: N*n大小的期望关节加速度轨迹
:param gtilde: 机器人模型的重力向量
:param Mtildelist: 机器人模型的零位的i-1系中i系的位姿(位置矩阵)
:param Gtildelist: 机器人模型的空间惯量矩阵
:param Kp: PID的Kp项
:param Ki: PID的Ki项
:param Kd: PID的Kd项
:param dt: 轨迹中间隔控制点之间的时间间隔,即控制周期
:param intRes: 如ForwardDynamicsTrajectory函数中,作为前向动力学轨迹的积分步的数目
:return taumat: 返回N*n的指令关节力矩轨迹
:return thetamat: 返回N*n的实际关节位置轨迹我们可以看到,对于gtilde,Mtildelist,Gtildelist, 代表机器人模型的相关参数,而这些参数可能是错误的。
而之前给到的g,Mlist,Slist则是真正的参数。
我们正是要用这种可能错误的模型进行控制推算,而代码这边进行仿真用真实的参数,这样才能模拟出一个仿真器,进而得到误差,走我们的动力学PID控制流程。
如果不采用两组参数(一组真实参数,一组模型参数),那就无法在这里进行仿真,走PID控制流程了。
这点请读者们要了解,这是在模拟一个仿真器,不代表要用户傻傻的,明知道真实参数却使用错误参数。这里假设用户是不知道真实参数的。
首先,我们调用上一个函数 ComputedTorque,计算特定时刻的关节力矩:
for i in range(n):
taulist \
= ComputedTorque(thetacurrent, dthetacurrent, eint, gtilde, \
Mtildelist, Gtildelist, Slist, thetamatd[:, i], \
dthetamatd[:, i], ddthetamatd[:, i], Kp, Ki, Kd)注意这个时候用的变量是gtilde,Mtildelist,Gtildelist,也就是说这个时刻算出来的是根据模型得到的期望控制力矩。这里假设我们用户只知道一个模型的值。我们把这个函数中送入期望的位置、期望的速度、期望的加速度,计算此时的期望控制力矩。
接下来我们执行仿真的步骤(这里是仿真,模拟一个仿真器的运行流程):
for j in range(intRes):
ddthetalist \
= ForwardDynamics(thetacurrent, dthetacurrent, taulist, g, \
Ftipmat[:, i], Mlist, Glist, Slist)
thetacurrent, dthetacurrent \
= EulerStep(thetacurrent, dthetacurrent, ddthetalist, \
1.0 * dt / intRes)那么我们就需要根据指令力矩,推算机械臂的轨迹,这个和 ForwardDynamicsTrajectory函数中的实现基本上一致。当然由于我们实际执行的参数g,Mlist,Glist和模型参数gtilde,Mtildelist,Gtildelist不一致,加上欧拉积分本来也有误差,因此得到的位置、速度和期望的有所区别。 (注意,内循环这里起到一个仿真的作用)
那仿真完毕以后,需要计算如下的值:(注意,此时还在外循环i里:)
taumat[:, i] = taulist
thetamat[:, i] = thetacurrent
eint = np.add(eint, dt * np.subtract(thetamatd[:, i], thetacurrent))所以thetamat代表实际执行的值,而thetamatd代表期望的控制轨迹,相减并积分得到PID控制中的积分项。
把各轮走完以后呢,自然就得到最后的输出:指令关节力矩,和实际的关节位置轨迹了。
剩下的代码是画图,这个用默认的样例跑完以后呢,结果如下:

我们可以看到,尽管我们利用ComputedTorque函数,送入的都是我们所掌握的不太精确的参数,和实际机器人参数有出入,但是利用这样的控制率,我们仍然能够追上或者接近用户期望的轨迹,这恰恰就是控制的精髓所在了。
耗费时长快3个月,终于抽空把这个快烂尾的文章写完了。说来惭愧。
希望我的笔记可以给大家一些参考。
专栏地址:
【现代机器人学】学习笔记
近期我还会更新一篇关于现代机器人学这本书中我发现的一些翻译、或者描述不太准确的地方(我自认为的),再之后就不会再写新的关于《现代机器人学-机构、规划与控制》的博文了。
后面我的计划是,先更新一版《C++并发编程》的学习笔记,然后同时去学习另一本书,这是一位我非常要好的同事,一位来自浙大的技术大佬,我的良师益友Yang Liangzhu推荐的,叫《机器人学-建模、规划与控制》。这本书我大概看了看,觉得写的非常的好,不过不是用旋量体系写的。但内容的广度和厚度也比现代机器人学厚很多。文章来源:https://www.toymoban.com/news/detail-663473.html
请大家多多关注。文章来源地址https://www.toymoban.com/news/detail-663473.html
到了这里,关于【现代机器人学】学习笔记十三:配套代码解析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!