1. Toy模板网首页
  2. > Toy博客

【数据结构】二叉树的链式结构的实现 -- 详解

9月前 作者：炫酷的伊莉娜 分类：Toy博客 阅读(42) 违法举报

这篇具有很好参考价值的文章主要介绍了【数据结构】二叉树的链式结构的实现 -- 详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、前置说明

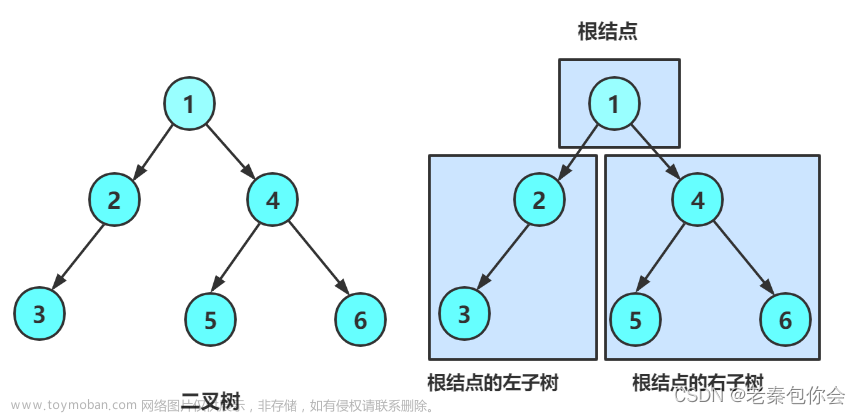
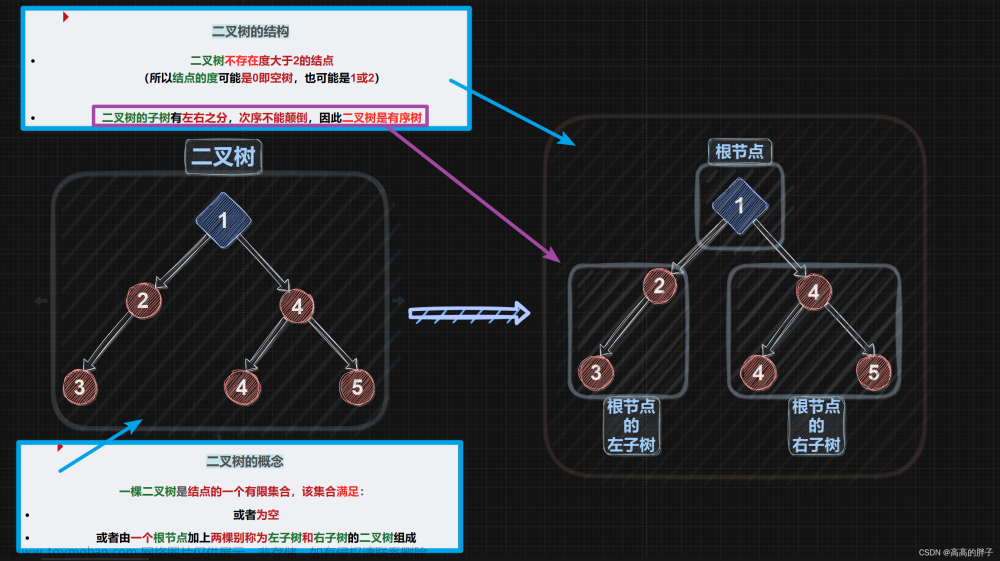
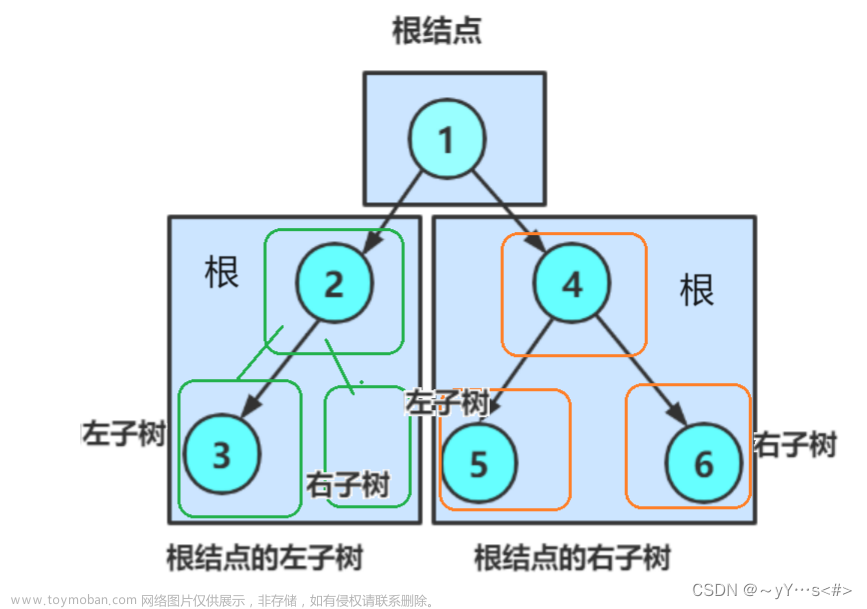
在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习。 
typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

// 动态申请一个新节点
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	assert(newnode);

	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;

	return newnode;
}

BTNode* CreatBinaryTree()
{
    BTNode* node1 = BuyNode(1);
    BTNode* node2 = BuyNode(2);
    BTNode* node3 = BuyNode(3);
    BTNode* node4 = BuyNode(4);
    BTNode* node5 = BuyNode(5);
    BTNode* node6 = BuyNode(6);
 
    node1->left = node2;
    node1->right = node4;
    node2->left = node3;
    node4->left = node5;
    node4->right = node6;
    return node1;
}

注意：上述代码并不是创建二叉树的方式。

二、构建二叉树

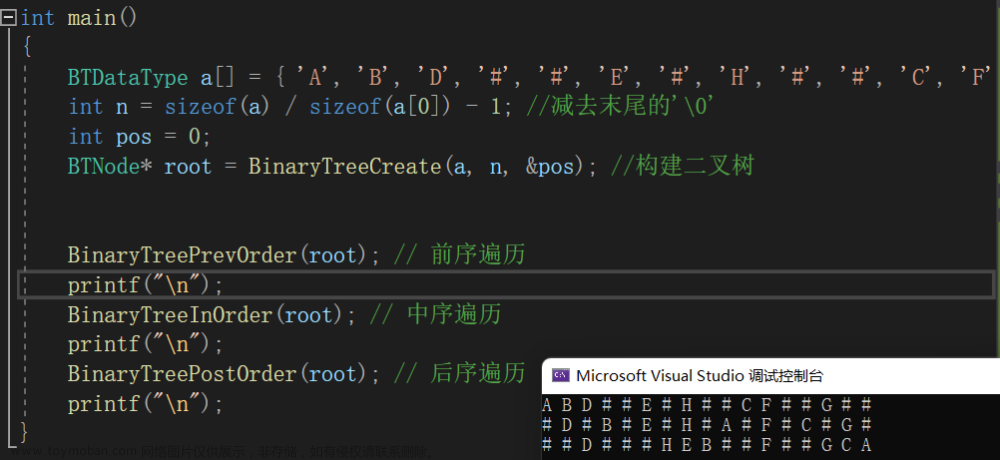
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (*pi >= n)
	{
		return NULL;
	}

	char ch = a[*pi];
	(*pi)++;

	if (ch == '#')
	{
		return NULL;
	}

	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	newNode->data = ch;
	newNode->left = BinaryTreeCreate(a, n, pi);
	newNode->right = BinaryTreeCreate(a, n, pi);

	return newNode;
}

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

三、二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历 (Traversal) 是按照某种特定的规则，依次对二叉 树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
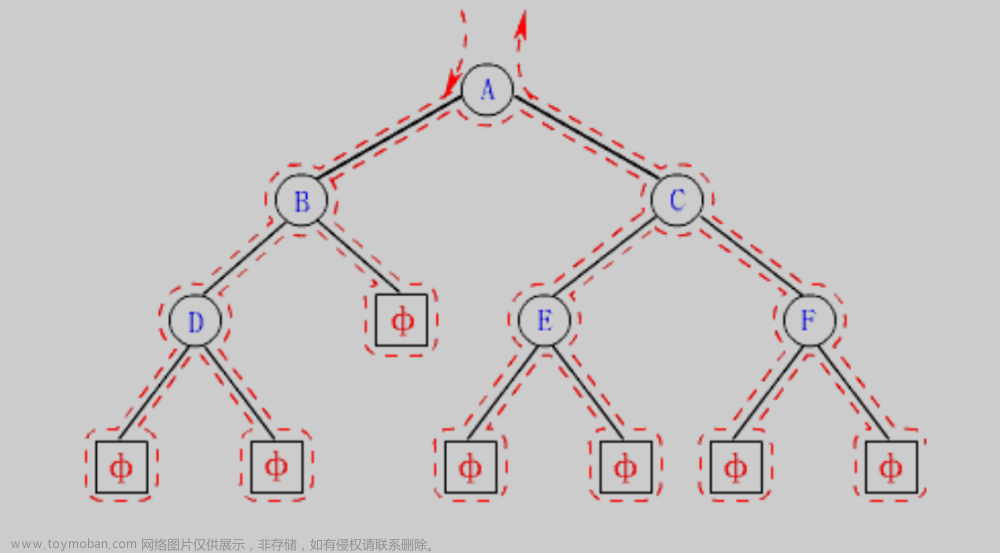
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

二叉树的遍历方式主要有四种，先介绍三种，最后再介绍第四种。（利用了分治的思想）

  1. 前序遍历 (Preorder Traversal 亦称先序遍历)，方式为先遍历根结点，左子树，右子树。
  2. 中序遍历 (Inorder Traversal)，方式为先遍历左子树，根结点，右子树。
  3. 后序遍历 (Postorder Traversal)，方式为先遍历左子树，右子树，根结点。
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);

其中这三种遍历方式一般都用递归进行实现。

由于被访问的结点必是某子树的根，所以 N(Node）、L(Left subtree）和 R(Right subtree）又可解释为 根、根的左子树和根的右子树。NLR、LNR 和 LRN分别又称为先根遍历、中根遍历和后根遍历。
注意 ：
  1. 深度优先遍厉：前序遍厉、中序遍厉、后序遍厉，注意有些说法只认同前序遍厉。
  2. 广度优先遍厉：层序遍厉。

1、前序遍历

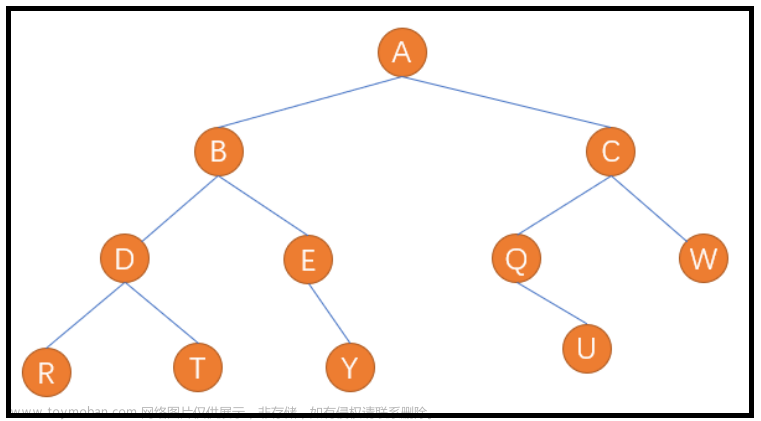
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

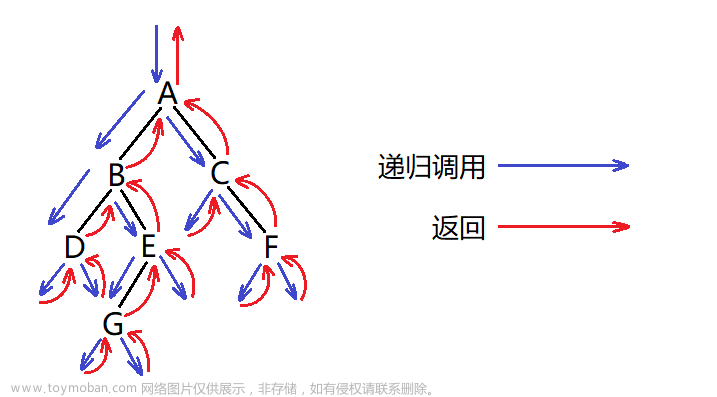
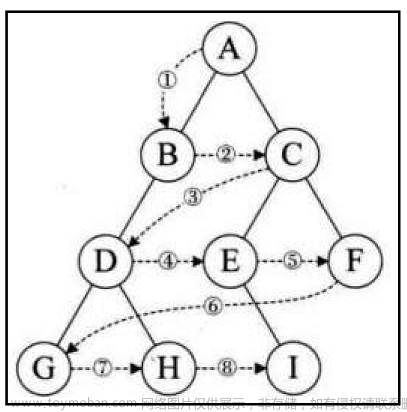
按照前序遍历的方式，我们应该先遍历根结点 A，然后再去遍历左子树。当进入左子树后，我们需要再执行前序遍历方式，即遍历 A 的左子树中的根结点 B，然后再遍历 B 的左子树。当我们再进入左子树，又是先遍历根结点D，然后又遍历左子树，按照顺序遍历到 R，此时终于完成根结点，左子树，接下来遍历右子树。进入右子树后，又遍历根结点T... ...，所以这种遍历方式属于递归性质的。（遍历顺序为：A–>B–>D–>R–>T–>E–>Y–>C–>Q–>U–>W）

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root) // 根->左子树->右子树
{
	if (root == NULL)
	{
		printf("# "); // 用#代表NULL
		return;
	}
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
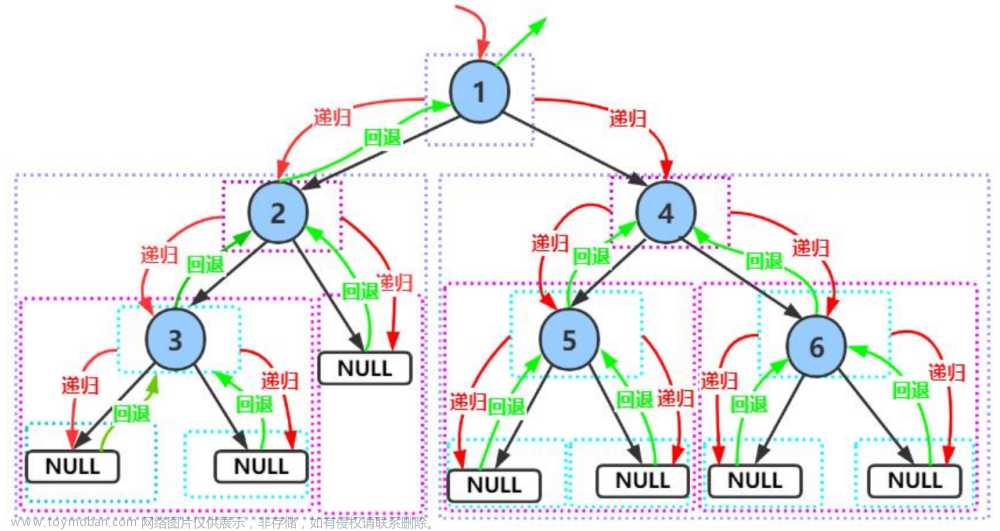
	BinaryTreePrevOrder(root->right);
}
【递归图解】
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

2、中序遍历

中序遍历方式为左子树，根结点，右子树。仍以上面的图为例，遍历顺序为：

R–>D–>T–>B–>E–>Y–>A–>Q–>U–>C–>W

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)// 左子树->根->右子树
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);
	BinaryTreeInOrder(root->right);
}

3、后序遍历

后序遍历方式为 左子树，右子树，根结点。仍以上面的图为例，遍历顺序应该为：

R–>T–>D–>Y–>E–>B–>U–>Q–>W–>C–>A

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) // 左子树->右子树->根
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);
}

【总结】 

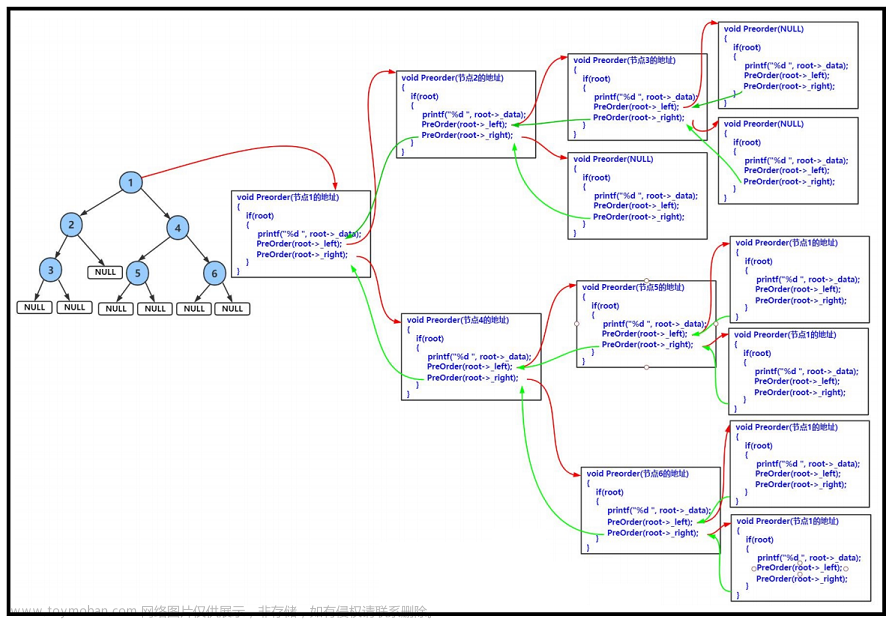
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习
  • 前序遍历结果：1->2->3->4->5->6
  • 中序遍历结果：3->2->1->5->4->6
  • 后序遍历结果：3->2->5->6->4->1

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

4、层序遍历

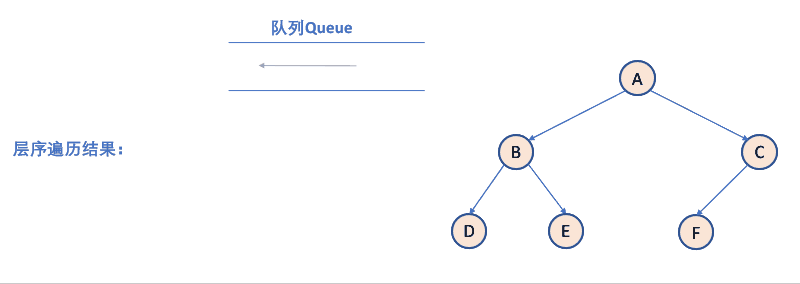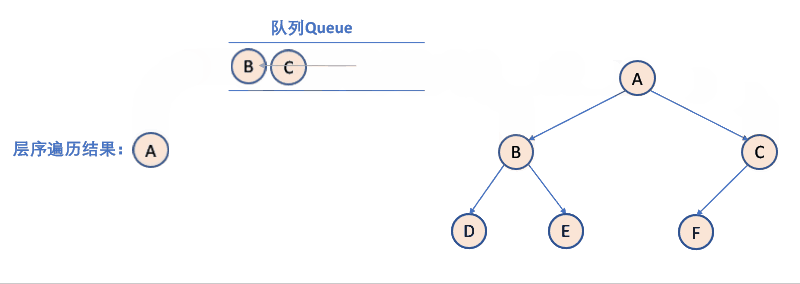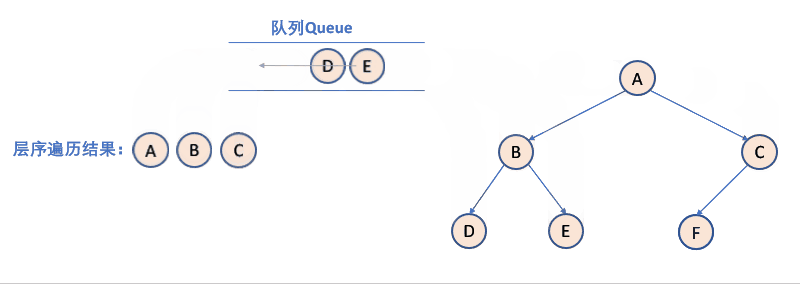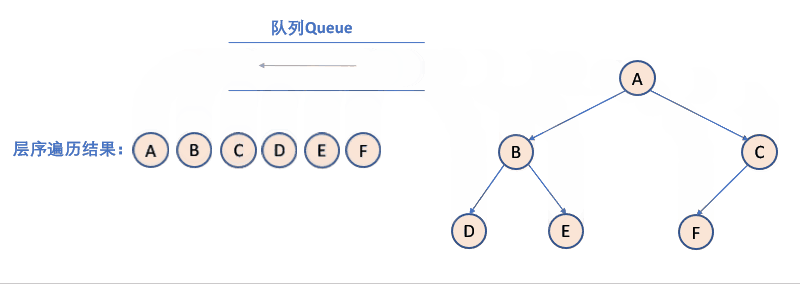
层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。
设二叉树的根节点所在层数为 1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第 2 层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习 
// 层序遍历
void LevelOrder(BTNode* root);

注意：层序遍历一般需要使用队列。 （队列内容前面已经详细介绍过了）

【思路】先让根入队列，然后再让根出队列，当左子树不为 NULL 时让左子树入队列，当右子树不为NULL时让右子树入队列，然后不断地迭代下去，直至队列为空。记得出队列前要保存当前值来访问到该元素，Pop 到队列当中的值是地址，通过该地址来访问其中的 data。

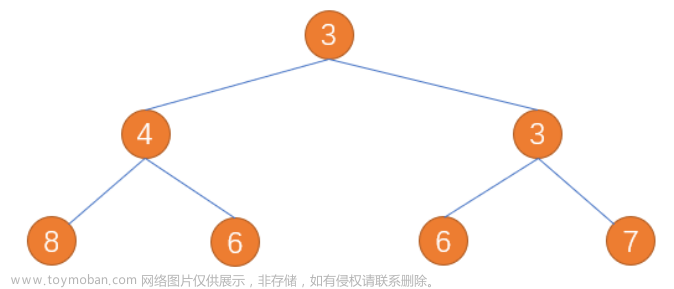
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

层序遍历结果为： 3->4->3->8->6->6->7

如何利用队列实现呢？
  1. 判断当前队列是否为空。
  2. 队列为空：结束；队列非空：取出队列第一个元素入队列。
  3. 上一层出来后，再入下一层（即它的左右孩子节点）。

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

由于前面已经对队列的各种操作进行了详解，这里就不展开讲了。（直接运用之前写的 Queue.c 和 Queue.h）

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root) // 树的根节点root不为空 将根节点入队列
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); // 获取队列头部元素
		printf("%c ", front->data); // 打印节点值
		QueuePop(&q); // 出队列

		// 如果当前树根的左右孩子不为空 则分别入队列
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习​

四、二叉树其它接口的实现

1、二叉树的节点个数

按照递归的思想，计算二叉树的节点数量，我们可以认为 二叉树的节点个数 = 左子树数量 + 右子树数量 + 1，其中 1 是当前根节点数量（前提条件是存在根节点）。

【思想 1】

迭代，使用栈来模拟递归的过程，用全局变量 / 静态局部变量来记录节点个数，遍历二叉树的所有节点，并累加节点的个数。

【思想 2】

递归，利用分治的思想，函数使用带返回值的方式，其内部的递归本质上是一个后序遍厉（左子树->右子树->根节点）。

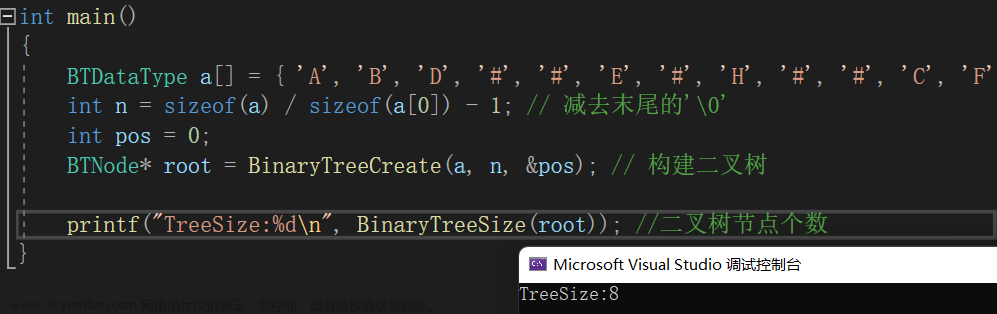
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习​

2、二叉树叶子节点个数

按照递归的思想，计算二叉树的叶子节点数量，我们可以认为 叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数 + 0，0 是因为当前根结点有子树，说明根结点不是叶子结点。

【思想】

以 left 和 right 为标志，如果都为 NULL，则说明该节点是叶子节点。

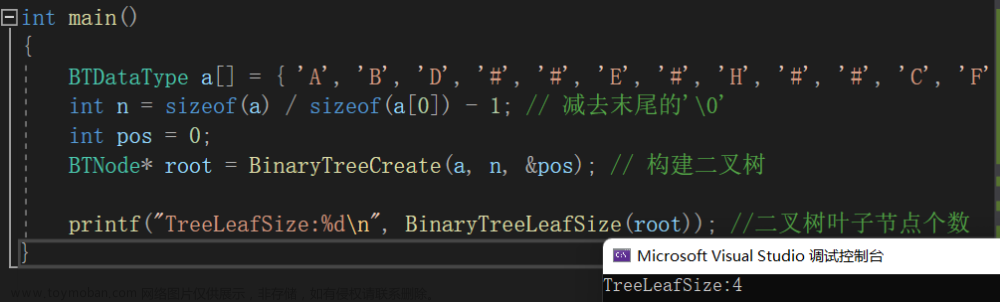
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
    // 先判断当前访问的节点是否为空
	if (root == NULL) 
	{
		return 0;
	}

    // 当前节点不为空，它的左右孩子都为空，说明该节点是叶子节点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

    // 当前节点不为空，左右孩子不都为空，则继续往下遍历
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习​

3、二叉树第k层节点个数

【思想】

求当前树的第 k 层节点个数 = 左子树的第 k-1 层节点个数 + 右子树的第 k-1 层节点个数 (当 k=1 时，说明此层就是目标层)

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习​

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL) // 先判断当前访问的节点是否为空
	{
		return 0;
	}

	if (k == 1) // 当前节点不为空，而k已经减到1了，说明遍历到了第k层，说明该节点是第k层的
	{
		return 1;
	}

    // 还没有遍历到第k层，我们就继续往下遍历
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
如何知道这个节点是不是第 k 层的？

求二叉树第 k 层的节点个数，我们从根节点开始往下遍历（按根->左->右的顺序），每遍历一次 k 就减 1一次，当 k==1 时，说明我们遍历到了第 k 层，此时访问该层的节点。如果它不为空，则二叉树第 k 层的节点个数就要 +1。

4、二叉树查找值为x的节点

【思想】

按照递归思想，先判断当前结点是否是目标节点，然后查找左子树，再查找右子树。

如果左右子树都没有找到，就返回NULL。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL) // 先判断当前访问的节点是否为空
	{
		return NULL;
	}

	if (root->data == x) // 判断要找的x值节点是不是当前节点
	{
		return root;
	}

    // 不是当前节点，则继续去该节点的左子树中找
	BTNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}

    // 还没找到，再继续去该节点的右子树中找
	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL; // 当前节点及其左右子树中都没找到，返回NULL
}

5、销毁二叉树

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	// 如果使用前中序遍历销毁，节点会先被销毁，变成随机值，就不知道它的左右子树位置了 所以采用后序遍历销毁
	if (*root == NULL)
	{
		return;
	}
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));
	free(*root);
	*root = NULL; // 将根节点设置为NULL 防止野指针
}

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

注意：如果这里使用前序遍历或中序遍历进行销毁，节点会先被销毁，变成随机值，就不知道它的左右子树位置了，所以应该采用后序遍历来销毁二叉树。

如果这里传进来的是一级指针，由于要在函数内改变形参的值，无法改变外部实参的值，所以我们需要在函数外置头节点指针为NULL。

6、判断二叉树是否是完全二叉树

【思想】

层序遍历时，把空节点也入队列。

  • 完全二叉树中，非空节点是连续的，则空节点是连续的。
  • 非完全二叉树中，非空节点不是连续的，则空节点不是连续的。

所以在出队时，判断一下，出到第一个空节点时，跳出循环；

在下面重新写一个循环继续出队，并检查出队元素：

  • 如果第一个空节点后面的全是空节点，说明是完全二叉树。
  • 如果第一个空节点后面的有非空节点，说明是非完全二叉树。

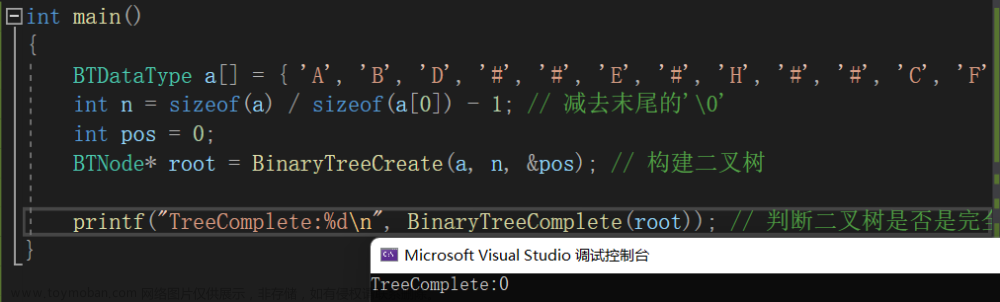
【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习​

// 判断二叉树是否是完全二叉树（利用层序遍历的思想来判断）
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root) // 树的根节点root不为空 将根节点入队列
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); // 获取队列头部元素
		QueuePop(&q); //出队列

		if (front)
		{
			// 不管当前树根的左右孩子是否为空，都分别入队列
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break; //遇到空后，跳出层序遍历
		}
	}

	// 如果后面全是空，则是完全二叉树，否则不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true; // 出队的节点中，如果没有出现非空节点，说明是完全二叉树出队的节点中，如果没有出现非空节点，说明是完全二叉树
}

【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习

五、代码整合

1、Queue.h

// Queue.h
#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

struct BinaryTreeNode;

typedef struct BinaryTreeNode* QDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
}Queue;

void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);

2、Queue.c

// Queue.c
#define _CRT_SECURE_NO_WARNINGS 1

#include "Queue.h"

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	newnode->data = x;
	newnode->next = NULL;
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	QNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;
	if (pq->head == NULL)
	{
		pq->tail = NULL;
	}
}

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}

QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

int QueueSize(Queue* pq)
{
	assert(pq);
	int n = 0;
	QNode* cur = pq->head;
	while (cur)
	{
		++n;
		cur = cur->next;
	}
	return n;
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

3、test.c

// test.c
#define _CRT_SECURE_NO_WARNINGS 1

#include "Queue.h"

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//动态申请一个新节点
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	assert(newnode);

	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;

	return newnode;
}

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (*pi >= n)
	{
		return NULL;
	}

	char ch = a[*pi];
	(*pi)++;

	if (ch == '#')
	{
		return NULL;
	}

	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	newNode->data = ch;
	newNode->left = BinaryTreeCreate(a, n, pi);
	newNode->right = BinaryTreeCreate(a, n, pi);

	return newNode;
}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
    // 先判断当前访问的节点是否为空
	if (root == NULL) 
	{
		return 0;
	}

    // 当前节点不为空，它的左右孩子都为空，说明该节点是叶子节点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

    // 当前节点不为空，左右孩子不都为空，则继续往下遍历
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL) // 先判断当前访问的节点是否为空
	{
		return 0;
	}

	if (k == 1) // 当前节点不为空，而k已经减到1了，说明遍历到了第k层，说明该节点是第k层的
	{
		return 1;
	}

    // 还没有遍历到第k层，我们就继续往下遍历
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL) // 先判断当前访问的节点是否为空
	{
		return NULL;
	}

	if (root->data == x) // 判断要找的x值节点是不是当前节点
	{
		return root;
	}

    // 不是当前节点，则继续去该节点的左子树中找
	BTNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}

    // 还没找到，再继续去该节点的右子树中找
	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL; // 当前节点及其左右子树中都没找到，返回NULL
}

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	// 如果使用前中序遍历销毁，节点会先被销毁，变成随机值，就不知道它的左右子树位置了 所以采用后序遍历销毁
	if (*root == NULL)
	{
		return;
	}
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));
	free(*root);
	*root = NULL; // 将根节点设置为NULL 防止野指针
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root) // 根->左子树->右子树
{
	if (root == NULL)
	{
		printf("# "); // 用#代表NULL
		return;
	}
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)// 左子树->根->右子树
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);
	BinaryTreeInOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) // 左子树->右子树->根
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);
}

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root) // 树的根节点root不为空 将根节点入队列
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); // 获取队列头部元素
		printf("%c ", front->data); // 打印节点值
		QueuePop(&q); // 出队列

		// 如果当前树根的左右孩子不为空 则分别入队列
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

// 判断二叉树是否是完全二叉树（利用层序遍历的思想来判断）
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root) // 树的根节点root不为空 将根节点入队列
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); // 获取队列头部元素
		QueuePop(&q); //出队列

		if (front)
		{
			// 不管当前树根的左右孩子是否为空，都分别入队列
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break; //遇到空后，跳出层序遍历
		}
	}

	// 如果后面全是空，则是完全二叉树，否则不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true; // 出队的节点中，如果没有出现非空节点，说明是完全二叉树出队的节点中，如果没有出现非空节点，说明是完全二叉树
}

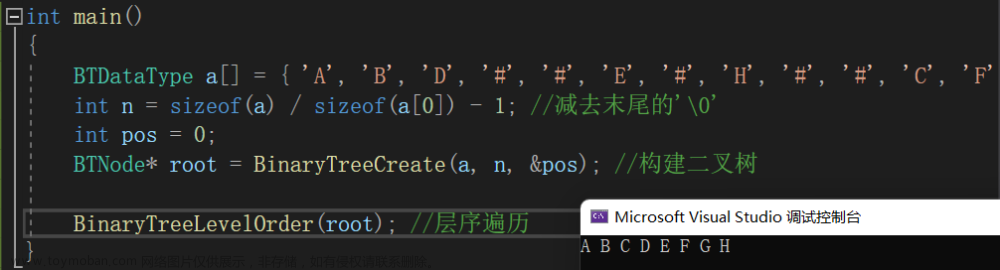
int main()
{
	BTDataType a[] = { 'A', 'B', 'D', '#', '#', 'E', '#', 'H', '#', '#', 'C', 'F', '#', '#', 'G', '#', '#' };
	int n = sizeof(a) / sizeof(a[0]) - 1; // 减去末尾的'\0'
	int pos = 0;
	BTNode* root = BinaryTreeCreate(a, n, &pos); // 构建二叉树

	printf("TreeSize:%d\n", BinaryTreeSize(root)); // 二叉树节点个数
	printf("TreeLeafSize:%d\n", BinaryTreeLeafSize(root)); // 二叉树叶子节点个数
	printf("Tree2LevelSize:%d\n", BinaryTreeLevelKSize(root, 2)); // 二叉树第k层节点个数
	printf("TreeFindB:%p\n", BinaryTreeFind(root, 'B')); // 二叉树查找值为x的节点
 
	// 前序遍历
	BinaryTreePrevOrder(root);
	printf("\n");
	// 中序遍历
	BinaryTreeInOrder(root);
	printf("\n");
	// 后序遍历
	BinaryTreePostOrder(root);
	printf("\n");
	BinaryTreeLevelOrder(root); // 层序遍历

	printf("TreeComplete:%d\n", BinaryTreeComplete(root)); // 判断二叉树是否是完全二叉树
	BinaryTreeDestory(&root);// 二叉树销毁
	printf("二叉树已销毁\n");
	return 0;
}

六、程序运行整体效果

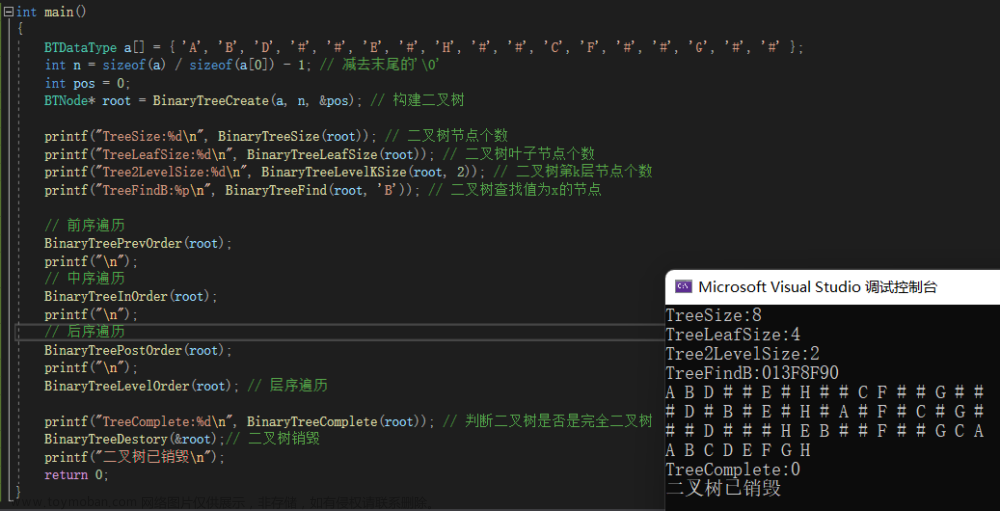【数据结构】二叉树的链式结构的实现 -- 详解,数据结构,C语言,初学者,c语言,数据结构,学习文章来源地址https://www.toymoban.com/news/detail-663639.html

到了这里，关于【数据结构】二叉树的链式结构的实现 -- 详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 【数据结构】二叉树的链式实现及遍历

    【数据结构】二叉树的链式实现及遍历

    后文所有代码中的二叉树结点： 前，中，后序遍历都可以采用分治递归的思想解决，将根节点和它的孩子结点分别处理。 此处仅利用递归展开图分析前序遍历，中序和后序也是相同的思想： 层序遍历需要利用队列来进行，如果二叉树跟结点不为空，则让 指向它的一个指针入

    2024年02月07日
    浏览(50)

  • 数据结构——二叉树的链式存储的实现

                             InitBiTree(BiTree T)——初始化二叉树。                         CreateBiTree(BiTree T)——先序遍历的顺序建立二叉链表。                         PreOrderTraverse(BiTree T)——先序遍历。                         

    2024年02月04日
    浏览(53)
  • 数据结构第六课 -----链式二叉树的实现

    数据结构第六课 -----链式二叉树的实现

    🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 ​🎂 作者介绍： 🎂🎂 🎂 🎉🎉🎉🎉🎉🎉🎉 🎂 🎂作者id：老秦包你会， 🎂 简单介绍：🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂 喜欢学习C语言和python等编程语言，是一位爱分享的博主，有兴趣的小可爱可以来互讨 🎂🎂

    2024年02月03日
    浏览(49)
  • 数据结构（C语言实现）——二叉树的概念及二叉树顺序结构和链式结构的实现（堆排序+TOP-K问题+链式二叉树相关操作）

    数据结构（C语言实现）——二叉树的概念及二叉树顺序结构和链式结构的实现（堆排序+TOP-K问题+链式二叉树相关操作）

    前面学习了数据结构中线性结构的几种结构，顺序表，链表，栈和队列等，今天我们来学习一种非线性的数据结构——树。由于二叉树是数据结构中的一个重点和难点，所以本文着重介绍二叉树的相关概念和性质，以及二叉树的应用。 树是一种非线性的数据结构，它是由n（

    2023年04月21日
    浏览(45)
  • 【数据结构初阶】八、非线性表里的二叉树（二叉树的实现 -- C语言链式结构）

    【数据结构初阶】八、非线性表里的二叉树（二叉树的实现 -- C语言链式结构）

    ========================================================================= 相关代码gitee自取 ： C语言学习日记: 加油努力 (gitee.com)  ========================================================================= 接上期 ： 【数据结构初阶】七、非线性表里的二叉树（堆的实现 -- C语言顺序结构）-CSDN博客  ==========

    2024年02月08日
    浏览(52)
  • 【链式二叉树】数据结构链式二叉树的（万字详解）

    【链式二叉树】数据结构链式二叉树的（万字详解）

    前言： 在上一篇博客中，我们已经详解学习了堆的基本知识，今天带大家进入的是二叉树的另外一种存储方式----“链式二叉树”的学习，主要用到的就是“递归思想”！！ 前情回顾： 再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是： 空树 非空：根节点，根节点

    2024年01月20日
    浏览(51)
  • 数据结构——二叉树的链式结构

    数据结构——二叉树的链式结构

      个人主页 ： 日刷百题 系列专栏 ： 〖C语言小游戏〗〖Linux〗〖数据结构〗  〖C语言〗 🌎 欢迎各位 → 点赞 👍+ 收藏 ⭐️+ 留言 📝  ​ 这里我们使用先序遍历的思想来创建二叉树，这里的内容对于刚接触二叉树的朋友可能有些难理解，不妨先看完下面的二叉树各种遍历

    2024年02月05日
    浏览(48)
  • 【数据结构】二叉树的链式结构

    【数据结构】二叉树的链式结构

    学习链式二叉树要知道三种遍历方式，便于对二叉树的节点以及左子树和右子树进行操作。 前序遍历：根、左子树、右子树 中序遍历：左子树、根、右子树 后序遍历：左子树、右子树、根 以下图为例： 得到的结果： 前序遍历：1 2 3 4 5 6 中序遍历：3 2 1 5 4 6 后序遍历：3 2

    2024年02月08日
    浏览(57)
  • 数据结构：二叉树的链式结构

    数据结构：二叉树的链式结构

    朋友们、伙计们，我们又见面了，本期来给大家解读一下链式二叉树的相关知识点，如果看完之后对你有一定的启发，那么请留下你的三连，祝大家心想事成！ 数据结构与算法专栏 ：数据结构与算法 个  人  主  页 ：stackY、 C 语 言 专 栏 ：C语言：从入门到精通 目录 前言

    2024年02月07日
    浏览(59)
  • 【数据结构】二叉树的链式存储结构

    【数据结构】二叉树的链式存储结构

    前序遍历，又叫先根遍历。 遍历顺序：根 - 左子树 - 右子树 代码： 中序遍历，又叫中根遍历。 遍历顺序：左子树 - 根 - 右子树 代码 ： 后序遍历，又叫后根遍历。 遍历顺序：左子树 - 右子树 - 根 代码 ： 除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍

    2024年02月09日
    浏览(46)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包