❓ 剑指 Offer 10- I. 斐波那契数列
难度:简单
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
提示:
0 <= n <= 100
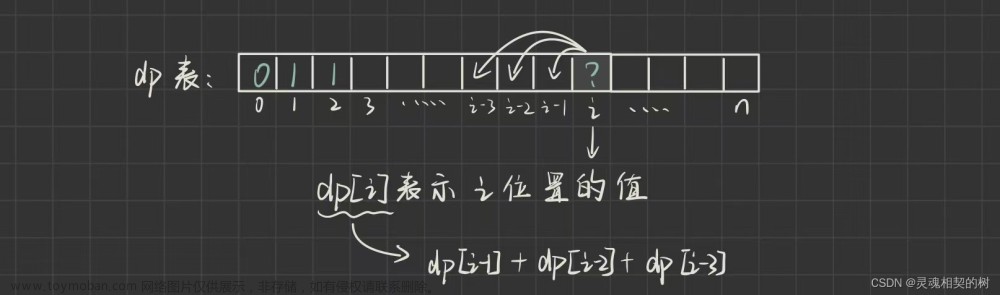
💡思路:动态规划
如果使用递归求解,会重复计算一些子问题。
-
例如,计算
f(4)需要计算f(3)和f(2),计算f(3)需要计算f(2)和f(1),可以看到f(2)被重复计算了。
-
递归是将一个问题划分成多个子问题求解,动态规划也是如此,
-
但是 动态规划会把子问题的解缓存起来,从而 避免重复求解子问题。
优化:
- 考虑到第
i项只与第i-1和第i-2项有关,因此只需要存储前两项的值就能求解第i项,从而将空间复杂度由O(n)降低为O(1)。
🍁代码:(C++、Java)
C++
class Solution {
public:
int fib(int n) {
if(n <= 1) return n;
vector<int> fib(n + 1);
fib[1] = 1;
for(int i = 2; i <= n; i++){
fib[i] = (fib[i - 1] + fib[i - 2]) % 1000000007;
}
return fib[n] ;
}
};
Java
class Solution {
public int fib(int n) {
if(n <= 1) return n;
int[] fib = new int[n + 1];
fib[1] = 1;
for(int i = 2; i <= n; i++){
fib[i] = (fib[i - 1] + fib[i - 2]) % 1000000007;
}
return fib[n] ;
}
}
优化:
C++
class Solution {
public:
int fib(int n) {
if(n <= 1) return n;
int pre1 = 0, pre2 = 1, tmp = 0;
for(int i = 2; i <= n; i++){
tmp = (pre1 + pre2) % 1000000007;
pre1 = pre2;
pre2 = tmp;
}
return tmp;
}
};
Java
class Solution {
public int fib(int n) {
if(n <= 1) return n;
int pre1 = 0, pre2 = 1, tmp = 0;
for(int i = 2; i <= n; i++){
tmp = (pre1 + pre2) % 1000000007;
pre1 = pre2;
pre2 = tmp;
}
return tmp;
}
}
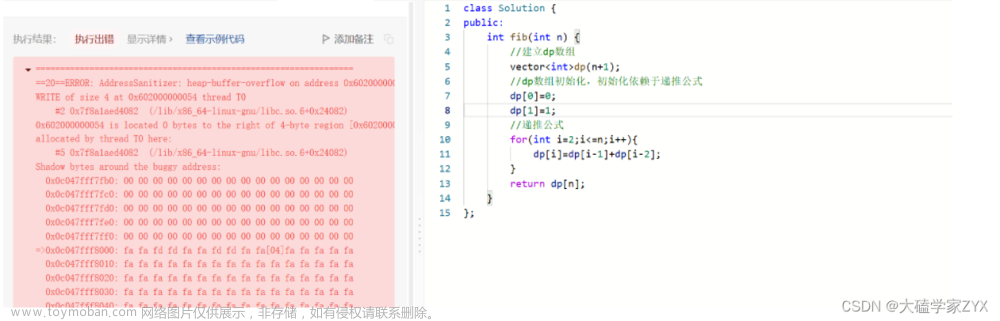
🚀 运行结果:

🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
题目来源:力扣。文章来源:https://www.toymoban.com/news/detail-664421.html
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!文章来源地址https://www.toymoban.com/news/detail-664421.html
注: 如有不足,欢迎指正!
到了这里,关于(动态规划) 剑指 Offer 10- I. 斐波那契数列 ——【Leetcode每日一题】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!