加权最小二乘WLS融合/简单凸组合SCC融合——多传感器分布式融合算法
原创不易,路过的各位大佬请点个赞
主要讲解算法:
加权最小二乘融合WLS
简单凸组合融合SCC
应用于: 多传感器网络协同目标跟踪/定位/导航
联系WX: ZB823618313
1. 分布式航迹融合
根据系统需求(成本、安全性、可维护性等)以及外界环境(自然环境、人为对抗环境),信息融合系统的结构一般可划分为:集中式结构、分布式结构以及混合式结构。
分布式航迹融合也称为传感器级融合或自主式融合。在这种结构中,每个传感器都有自己的处理器,进行一些预处理,然后把中间结果送到中心节点, 进行融合处理。由于各传感器都具有自己的局部处理器,能够形成局部航迹,所以在融合中心也主要是对局部航迹进行融合,所以这种融合方法通常也称为航迹融合(track fusion)。
这种结构因对信道要求低、系统生命力强、工程上易于实现、且对融合中心的计算能力要求低。
从不同的角度,分布式融合也可以分为不同类型。分布式结构也可以分为三种形式:
1)有融合中心的分布式结构
2)无融合中心,共享航迹的分布式结构
3)无融合中心,共享关联量测的分布式结构。`
笔记:
多传感器分布式融合也是估计融合领域最热门的邻域之一,也是目前两大学者在融合邻域关注的焦点
此外,分布式融合算法种类非常多,研究角度也各不相同。换句话说,分布式融合本身就是一个非常大的方向
本博客主要介绍分布式融合中最常用、最普遍的一种算法:加权最小二乘融合/简单凸组合融合
分布式航迹融合算法非常众多:
- 简单凸组合SCC融合算法
- 加权最小二乘WLS融合
- 协方差交叉CI融合算法
- 分布式信息滤波器算法
- Bar-Shalom-Campo融合算法
- 联邦卡尔曼滤波器算法
- …
本博客主要讲前两种融合算法。实际上它们可以被认为是一种融合算法的不同叫法。它们的理论是一样的,即、利用局部估计的协方差对局部估计进行加权融合得到全局估计。
下面主要介绍WLS 和SCC融合的优势和缺点,以及它们比较适用的场景。
2. 加权最小二乘WLS融合
加权最小二乘WLS融合是最简单、最容易实现、鲁棒性最高、工程应用最广泛的分布式融合算法之一。
2.1 从分布式融合挑战——到——加权最小二乘WLS融合
由于航迹融合中各传感器局部估计误差相关、各传感器量测噪声相关、局部动态模型不同以及系统的网络结构和信息模式复杂等因素,导致分布式融合算法的设计和开发变得极为复杂。
这些因素一般直接影响算法的融合精度、计算效率、融合器的鲁棒性等等。
是在实际工程中,各个传感器在不同的区域分布。它们相对独立地工作和观测目标,可以忽略各传感器之间噪声的相关性。
此外,局部估计误差之间的相关性一般是未知的。这些信息在融合过程无法利用。
从而加权最小二乘WLS融合算法应运而生。它忽略了局部估计误差的相关性和各传感器量测噪声的相关性,得到一种结构简单且计算效率高的解析融合器。
加权最小二乘WLS融合算法应该是工程中应用最广泛和最成功的融合算法之一。这也是为什么它是最经典的分布式哦
2.2 加权最小二乘WLS融合结构
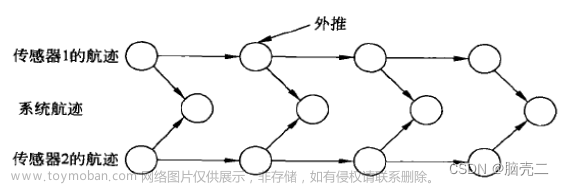
下图为加权最小二乘WLS融合算法的结构图。从图中可以看出,各个局部传感器向融合传输局部估计及其协方差。融合中心统一融合处理接受的局部估计及其协方差。
\
特点1)加权最小二乘WLS融合中通信是单向的,即局部传感器向融合中心传输处理后的信息,而融合中心不向局部传感器传输任何信息;
2)各个局部传感器独立工作,无任何协作;
3)融合中心只需要局部估计和它对应的协方差;
4)单个局部传感器的损坏并不影响全局估计的工作;
2.3 加权最小二乘WLS融合算法
2.3.1 问题描述:目标运动和量测模型
假设有 M M M个传感器用于观测同一个目标, 且目标状态转移方程为
x k = f ( x k − 1 ) + w k − 1 (1) x_k=f(x_{k-1}) +w_{k-1} \tag{1} xk=f(xk−1)+wk−1(1)
其中 x k x_k xk目标在 k k k时刻的状态, w k − 1 w_{k-1} wk−1过程噪声。
传感器量测方程为
z k i = h ( x k ) + v k i (2) z_k^i=h(x_k)+v_k^i \tag{2} zki=h(xk)+vki(2)
其中 z k i z_k^i zki为第 i i i个传感器在 k k k时刻的量测数据, v k i v_{k}^i vki第 i i i个传感器的量测噪声。
一般假设
w
k
w_k
wk和
v
k
v_k
vk为零均值高斯白噪声,其方差分别为
Q
k
Q_k
Qk和
R
k
R_k
Rk的高斯白噪声,即
w
k
∼
(
0
,
Q
k
)
w_k\sim(0,Q_k)
wk∼(0,Qk),
v
k
∼
(
0
,
R
k
)
v_k\sim(0,R_k)
vk∼(0,Rk),且满足如下关系(线性高斯假设)为:
E
[
w
i
v
j
′
]
=
0
E
[
w
i
w
j
′
]
=
0
i
≠
j
E
[
v
i
v
j
′
]
=
0
i
≠
j
\begin{aligned} E[w_iv_j'] &=0\\ E[w_iw_j'] &=0\quad i\neq j \\ E[v_iv_j'] &=0\quad i\neq j \end{aligned}
E[wivj′]E[wiwj′]E[vivj′]=0=0i=j=0i=j
2.3.2 局部估计(航迹)生成
每个传感器的利用观测到的数据实现目标状态的估计。定义
x
^
k
∣
k
i
,
P
k
∣
k
i
\hat{x}_{k|k}^i, {P}_{k|k}^i
x^k∣ki,Pk∣ki
为传感器
i
i
i产生的目标的局部估计和协方差。总共有
M
M
M个传感器,因此就有
M
M
M个类似的局部估计。这些局部估计都被传送融合中心进行融合处理。
如何产生这些局部航迹,则是一个经典的滤波问题:
- 如果(1)和(2)都是线性的,用卡尔曼滤波KF/鲁棒卡尔曼滤波产生
- 如果(1)和(2)都是非线性的,用EKF/UKC/CKF/QKF/CDKF/DDF/SRQUKF/PF等
非线性滤波参见专栏:非线性滤波-目标跟踪应用 //https://blog.csdn.net/weixin_44044161/category_11056621.html- 如果是机动目标跟踪,同交互式多模型IMM等等
IMM参见专栏:非线性滤波-目标跟踪应用 //https://blog.csdn.net/weixin_44044161/category_10931736.html
2.3.3 加权最小二乘WLS融合
融合中心利用某种融合算法对接受的 M M M个传感器的局部估计及其协方差进行融合处理,得到最终的全局估计及其协方差。
加权最小二乘WLS融合算法为:
x ^ k ∣ k = ( ∑ i = 1 M ( P k ∣ k i ) − 1 ) − 1 x ^ k ∣ k i P k ∣ k = ( ∑ i = 1 M ( P k ∣ k i ) − 1 ) − 1 \hat{x}_{k|k}=\Big(\sum_{i=1}^M({P}_{k|k}^i)^{-1}\Big)^{-1} \hat{x}_{k|k}^i\\ {P}_{k|k}=\Big(\sum_{i=1}^M({P}_{k|k}^i)^{-1}\Big)^{-1} x^k∣k=(i=1∑M(Pk∣ki)−1)−1x^k∣kiPk∣k=(i=1∑M(Pk∣ki)−1)−1
由于简单凸联合融合算法实现起来特别容易,所以它得到了广泛的应用。
然而,当各传感器的局部估计误差相关时,它是次优的。例如,当其中一个航迹是系统航迹,而另一个为传感器航迹时,或者当存在过程噪声时,就是这种情况。
但是,当两条航迹都是传感器航迹并且不存在过程噪声,两个传感器在初始时刻的估计误差也不相关时,简单凸联合融合算法则是最优的。也就是说,它能够得到和中心式融合相同的结果。
加权最小二乘WLS融合 简单吧!!!!!!!!!!!!!!!!!!!!
2.4 简单凸组合SCC融合算法
实际上,简单凸组合SCC融合和加权最小二乘WLS融合是同一种算法。SCC的原理和WLS的原理一样。好比同一个人有不同的名字。
3. 实验场景
讲了这么多,还不如直接弄一个实例。
既然是第一篇关于分布式融合的博客,实例直接上比较复杂的。哈哈哈哈哈哈
3.1 算法种类
算法:基于简单凸组合SCC的容积卡尔曼滤波CKF
3.2 参数设置
**运动模型:
仅匀转弯CT模型 X = [ x , y , x ˙ , y ˙ , w ] T {X}=[x, y, \dot{x}, \dot{y}, w]^T X=[x,y,x˙,y˙,w]T
X k + 1 = [ 1 sin ( ω T ) ω 0 − 1 − cos ( ω T ) ω 0 0 cos ( ω T ) 0 − sin ( ω T ) 0 0 1 − cos ( ω T ) ω 1 sin ( ω T ) ω 0 0 sin ( ω T ) 0 cos ( ω T ) 0 0 0 0 0 1 ] X k + W k X_{k+1}=\begin{bmatrix}1&\frac{\sin(\omega T)}{\omega}&0&-\frac{1-\cos(\omega T)}{\omega}&0\\0&\cos(\omega T)&0&-\sin(\omega T)&0\\0&\frac{1-\cos(\omega T)}{\omega}&1&\frac{\sin(\omega T)}{\omega}&0\\0&\sin(\omega T)&0&\cos(\omega T)&0\\0&0&0&0&1\end{bmatrix}X_{k} + W_k Xk+1= 10000ωsin(ωT)cos(ωT)ω1−cos(ωT)sin(ωT)000100−ω1−cos(ωT)−sin(ωT)ωsin(ωT)cos(ωT)000001 Xk+Wk
其中 W k W_k Wk为零均值白噪声,其方差为:
Q k = q k 2 [ T 3 / 3 T 2 / 2 0 0 0 T 2 / 2 T 0 0 0 0 0 T 3 / 3 T 2 / 2 0 0 0 T 2 / 2 T 0 0 0 0 0 q w ] Q_k=q_k^2\begin{bmatrix}T^3/3&T^2/2&0&0& 0 \\T^2/2&T&0&0 &0\\0&0&T^3/3&T^2/2 &0 \\0&0& T^2/2&T&0\\0&0&0&0&q_w\end{bmatrix} Qk=qk2 T3/3T2/2000T2/2T00000T3/3T2/2000T2/2T00000qw
或者为(两种形式都可以用,下面一代码形式给出)
传感器: 多个主动雷达
在二维情况下,雷达量测为距离和角度
r k m = r k + r ~ k b k m = b k + b ~ k {r}_k^m=r_k+\tilde{r}_k\\ b^m_k=b_k+\tilde{b}_k rkm=rk+r~kbkm=bk+b~k
其中
r k = ( x k − x 0 ) + ( y k − y 0 ) 2 ) b k = tan − 1 y k − y 0 x k − x 0 r_k=\sqrt{(x_k-x_0)^+(y_k-y_0)^2)}\\ b_k=\tan^{-1}{\frac{y_k-y_0}{x_k-x_0}}\\ rk=(xk−x0)+(yk−y0)2)bk=tan−1xk−x0yk−y0
[ x 0 , y 0 ] [x_0,y_0] [x0,y0]为雷达坐标,一般情况为0。雷达量测为 z k = [ r k , b k ] ′ z_k=[r_k,b_k]' zk=[rk,bk]′。雷达量测方差为
R k = cov ( v k ) = [ σ r 2 0 0 σ b 2 ] R_k=\text{cov}(v_k)=\begin{bmatrix}\sigma_r^2 & 0 \\0 & \sigma_b^2 \end{bmatrix} Rk=cov(vk)=[σr200σb2]
3.3 实验结果
3.3.1 跟踪轨迹
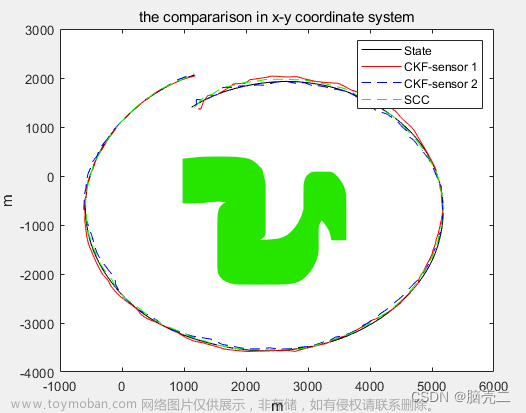
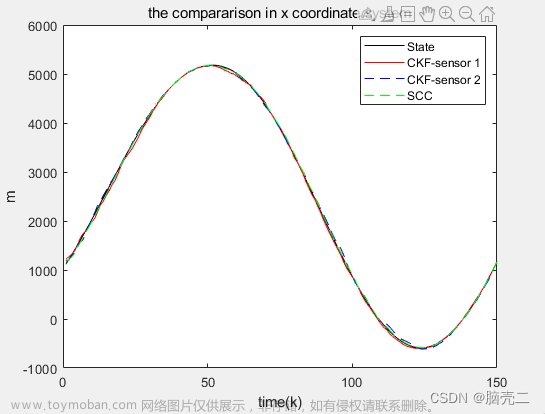
3.3.2 位置均方误差RMSE

3.3.2 位置均方误差RMSE
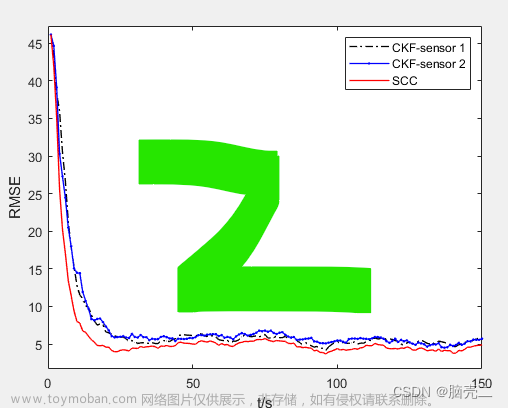 文章来源:https://www.toymoban.com/news/detail-665527.html
文章来源:https://www.toymoban.com/news/detail-665527.html
4. 部分代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% date:
% 任务:基于分布式融合算法的多雷达目标跟踪
% 一级算法:单雷达CKF
% 二级算法: 简单凸组合SCC融合
% 目标模型:CT
% 性能指标:跟踪轨迹,RMSE均方根误差
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;
close all;
clc;
%% initial parameter
n=4; %dimension of the target ;
T=1; %sample time
M=3; %number of rader
N=150; %the runs atime
MC=50; %Monte Carlo Runs
chan=4; %channel, for the class of fiter
w_mu=[0,0]'; % mean of process noise
v_mu=[0,0]'; % mean of measurement noise
%% target model
%covariance of process noise
q_x=1; %m/s^2
q_y=q_x;
Qk=diag([q_x^2,q_y^2]);
% state matrix
T_f=T; %sample time of fusion center
w=-pi/180*2.5;
Fk= [1 sin(w*T_f)/w 0 -(1-cos(w*T_f))/w
0 cos(w*T_f) 0 -sin(w*T_f)
0 (1-cos(w*T_f))/w 1 sin(w*T_f)/w
0 sin(w*T_f) 0 cos(w*T_f) ]; %
Gk= [ T_f^2/2 0
T_f 0
0 T_f^2/2
0 T_f ]; %
% covariance of measurement noise (radar)
% 雷达初始坐标及速度,可以自己设定,
xp(:,1)=[2, 0, 3 ,0 , 4, 0]; % %第一个传感器的位置,可设置[x坐标, 速度, y坐标, 速度,z坐标, 速度],xyz对应传感器三维位置中间的0不能变,只是为了适应维数
xp(:,2)=[4, 0, 7 ,0 , 3, 0];% %第2个传感器的位置[x坐标, 0, y坐标, 0,z坐标, 0]
xp(:,3)=[1, 0, 1 ,0 , 1, 0];% %第3个传感器的位置[x坐标, 0, y坐标, 0,z坐标, 0]
%% define parameter
sV=zeros(n,N,MC,1); % state
eV=zeros(n,N,MC,chan); %estimation
figure
plot(sV(1,:,1,1),sV(3,:,1,1),'-k',eV(1,:,1,1),eV(3,:,1,1),'-r',eV(1,:,1,2),eV(3,:,1,2),'--b',eV(1,:,1,3),eV(3,:,1,3),'--g')
xlabel('m');ylabel('m');
legend('State','CKF-sensor 1 ','CKF-sensor 2','SCC')
title('the compararison in x-y coordinate system')
figure;
ii=1:N;
plot(ii,sV(1,:,1,1),'k',ii,eV(1,:,1,1),'r',ii,eV(1,:,1,2),'--b',ii,eV(1,:,1,3),'--g');
xlabel('time(k)');ylabel('m');%zlabel('m');
legend('State','CKF-sensor 1 ','CKF-sensor 2','SCC')
title('the compararison in x coordinate system')
原创不易,路过的各位大佬请点个赞文章来源地址https://www.toymoban.com/news/detail-665527.html
到了这里,关于多传感器分布式融合算法——加权最小二乘WLS融合/简单凸组合SCC融合的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!












