一.简介

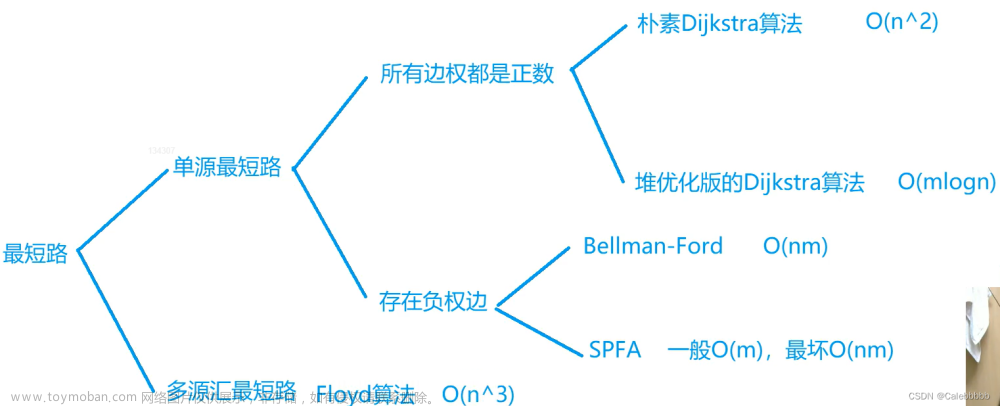
Floyd算法,也称为Floyd-Warshall算法,是一种用于解决所有节点对最短路径问题的动态规划算法。它可以在有向图或带权图中找到任意两个节点之间的最短路径。
Floyd算法的基本思想是通过中间节点逐步优化路径长度。它使用一个二维数组来存储任意两个节点之间的最短路径长度,并通过不断更新这个数组来得到最终的结果。
算法的步骤如下:
- 初始化一个二维数组,用于存储节点之间的最短路径长度。
- 将数组的初始值设置为图中节点之间的直接距离,如果两个节点之间没有直接连接,则距离为无穷大。
- 对于每个节点k,遍历所有节点对(i, j),并尝试通过节点k来优化路径长度。如果通过节点k可以获得更短的路径,则更新数组中的值。
- 重复步骤3,直到所有节点对的最短路径长度都被计算出来。
Floyd算法的时间复杂度为O(n^3),其中n是图中节点的数量。它适用于解决稠密图(边数接近节点数的平方)的最短路径问题,但对于稀疏图来说,可能存在更高效的算法。
总的来说,Floyd算法是一种非常经典且实用的算法,可以在有向图或带权图中找到任意两个节点之间的最短路径。
二.存图方法
因为是解决多源最短路,所以使用邻接矩阵存图。
三.原理
逐渐利用每个点进行搭桥,实现中转功能。过程中带有dp的思想,因为要使用搭完桥之后的最短路径进行再次搭桥,从而实现最优解。
四.核心代码
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);五.很重要的一道题
P1119 灾后重建 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
六.此题好的原因
考察了对选手floyd算法的进一步理解,而不是单纯的背板子
七.难点
最短路径是很好求的,但题目要求的时间是个大难题。有些路在一个时间点并不能用,更不能起到搭桥作用。所以输出答案时,并不能只考虑起点和终点不能走,还有考虑不能走对其他点最短路的影响。文章来源:https://www.toymoban.com/news/detail-665710.html
八.解决方案
既然没到时间就不能用这个点搭桥,那我们在计算整体最短路时不用不就行了吗?在floyd算法中,第一重遍历中的k就是用这个点进行搭桥,那我们就没到时间这前就不遍历即可。文章来源地址https://www.toymoban.com/news/detail-665710.html
九.参考代码
#include<iostream>
#include<cstdio>
#define N 205
using namespace std;
int n,m;
int a[N];
int f[N][N];//邻接矩阵存边
inline void updata(int k){
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(f[i][j]>f[i][k]+f[j][k])
f[i][j]=f[j][i]=f[i][k]+f[j][k];//用这个新的更新所有前面的
return;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++)
scanf("%d",a[i]);//依次输入每一个村庄建立完成时需要的时间
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
f[i][j]=1e9;//初始化为保证它不爆炸范围内的最大值
}
for(int i=0;i<n;i++)
f[i][i]=0;
int s1,s2,s3;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&s1,&s2,&s3);
f[s1][s2]=f[s2][s1]=s3;//初始化边长
}
int q;
cin>>q;
int now=0;
for(int i=1;i<=q;i++){//处理各询问
scanf("%d%d%d",&s1,&s2,&s3); //s3为可用时间点 ,s1为x点,s2为y点
while(a[now]<=s3&&now<n){
updata(now);//依次更新点,使它可以被用来更新其他的点
now++;
}
if(a[s1]>s3||a[s2]>s3)cout<<-1<<endl;
else {
if(f[s1][s2]==1e9)cout<<-1<<endl;
else cout<<f[s1][s2]<<endl;
}
}
return 0;
} 到了这里,关于【图论】Floyd算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!