系列文章目录
·【3D激光SLAM】LOAM源代码解析–scanRegistration.cpp
·【3D激光SLAM】LOAM源代码解析–laserOdometry.cpp
·【3D激光SLAM】LOAM源代码解析–laserMapping.cpp
·【3D激光SLAM】LOAM源代码解析–transformMaintenance.cpp
写在前面
本系列文章将对LOAM源代码进行讲解,在讲解过程中,涉及到论文中提到的部分,会结合论文以及我自己的理解进行解读,尤其是对于其中坐标变换的部分,将会进行详细的讲解。
本来是懒得写的,一个是怕自己以后忘了,另外是我在学习过程中,其实没有感觉哪一个博主能讲解的通篇都能让我很明白,特别是坐标变换部分的代码,所以想着自己学完之后,按照自己的理解,也写一个LOAM解读,希望能对后续学习LOAM的同学们有所帮助。
之后也打算录一个LOAM讲解的视频,大家可以关注一下。
整体框架
LOAM多牛逼就不用多说了,直接开始
先贴一下我详细注释的LOAM代码,在这个版本的代码上加入了我自己的理解。
我觉得最重要也是最恶心的一部分是其中的坐标变换,在代码里面真的看着头大,所以先明确一下坐标系(都是右手坐标系):
- IMU(IMU坐标系imu):x轴向前,y轴向左,z轴向上
- LIDAR(激光雷达坐标系l):x轴向前,y轴向左,z轴向上
- CAMERA(相机坐标系,也可以理解为里程计坐标系c):z轴向前,x轴向左,y轴向上
- WORLD(世界坐标系w,也叫全局坐标系,与里程计第一帧init重合):z轴向前,x轴向左,y轴向上
- MAP(地图坐标系map,一定程度上可以理解为里程计第一帧init):z轴向前,x轴向左,y轴向上
坐标变换约定: 为了清晰,变换矩阵的形式与《SLAM十四讲中一样》,即: R A _ B R_{A\_B} RA_B表示B坐标系相对于A坐标系的变换,B中一个向量通过 R A _ B R_{A\_B} RA_B可以变换到A中的向量。
首先对照ros的节点图和论文中提到的算法框架来看一下:


可以看到节点图和论文中的框架是一一对应的,这几个模块的功能如下:
- scanRegistration:对原始点云进行预处理,计算曲率,提取特征点
- laserOdometry:对当前sweep与上一次sweep进行特征匹配,计算一个快速(10Hz)但粗略的位姿估计
- laserMapping:对当前sweep与一个局部子图进行特征匹配,计算一个慢速(1Hz)比较精确的位姿估计
- transformMaintenance:对两个模块计算出的位姿进行融合,得到最终的精确地位姿估计
本文介绍transformMaintenance模块,它就是将laserOdometry和laserMapping两个模块优化得到的当前帧相对于初始帧的坐标变换进行融合,从而得到最终的最优的坐标变换结果。
一、变量含义
首先,介绍一下本程序用到变量的含义,与laserMapping一致:
- transformBefMapped[6]:从laserMapping模块接收到的,优化前的当前帧相对于初始时刻的位姿变换 T i n i t _ e n d T_{init\_end} Tinit_end
- transformSum[6]:从laserOdometry模块接收到的,当前帧相对于初始时刻的变换 T i n i t _ s t a r t T_{init\_start} Tinit_start
- transformAftMapped[6]:经过laserMapping模块优化后的,当前帧相对于初始时刻的位姿变换 T m a p _ e n d T_{map\_end} Tmap_end
- transformMapped[6]:融合后的当前帧相对于初始帧的坐标变换
一些理解:虽然transformAftMapped[6]我上面写的是 T m a p _ e n d T_{map\_end} Tmap_end,看起来好像是把坐标系换成了map坐标系,但是我觉得这里有两种理解都可以:
- AftMapped可以理解为经过laserMapping模块优化后的里程计坐标系下的当前帧end相对于初始帧的坐标变换
- 也可以理解为经过laserMapping模块优化,变到了map坐标系
二、main()函数
main函数依然很简单,就是定义了一些订阅者和发布者,接收/laser_odom_to_init和/aft_mapped_to_init两个坐标变换话题,然后进入相应的回调函数进行融合;然后发布融合后的当前帧相当于初始帧的坐标变换,以及坐标变换。
int main(int argc, char** argv)
{
ros::init(argc, argv, "transformMaintenance");
ros::NodeHandle nh;
ros::Subscriber subLaserOdometry = nh.subscribe<nav_msgs::Odometry>
("/laser_odom_to_init", 5, laserOdometryHandler);
ros::Subscriber subOdomAftMapped = nh.subscribe<nav_msgs::Odometry>
("/aft_mapped_to_init", 5, odomAftMappedHandler);
ros::Publisher pubLaserOdometry2 = nh.advertise<nav_msgs::Odometry> ("/integrated_to_init", 5);
pubLaserOdometry2Pointer = &pubLaserOdometry2;
laserOdometry2.header.frame_id = "/camera_init";
laserOdometry2.child_frame_id = "/camera";
tf::TransformBroadcaster tfBroadcaster2;
tfBroadcaster2Pointer = &tfBroadcaster2;
laserOdometryTrans2.frame_id_ = "/camera_init";
laserOdometryTrans2.child_frame_id_ = "/camera";
ros::spin();
return 0;
}
三、接收laserMapping的转换信息
接收/aft_mapped_to_init话题的回调函数很简单,就是将接收到的数据,赋值给transformAftMapped[6]和transformBefMapped[6]变量,这两个变量的含义与laserMapping中一致,就不过多解释了。
//接收laserMapping的转换信息
void odomAftMappedHandler(const nav_msgs::Odometry::ConstPtr& odomAftMapped)
{
double roll, pitch, yaw;
geometry_msgs::Quaternion geoQuat = odomAftMapped->pose.pose.orientation;
tf::Matrix3x3(tf::Quaternion(geoQuat.z, -geoQuat.x, -geoQuat.y, geoQuat.w)).getRPY(roll, pitch, yaw);
transformAftMapped[0] = -pitch;
transformAftMapped[1] = -yaw;
transformAftMapped[2] = roll;
transformAftMapped[3] = odomAftMapped->pose.pose.position.x;
transformAftMapped[4] = odomAftMapped->pose.pose.position.y;
transformAftMapped[5] = odomAftMapped->pose.pose.position.z;
transformBefMapped[0] = odomAftMapped->twist.twist.angular.x;
transformBefMapped[1] = odomAftMapped->twist.twist.angular.y;
transformBefMapped[2] = odomAftMapped->twist.twist.angular.z;
transformBefMapped[3] = odomAftMapped->twist.twist.linear.x;
transformBefMapped[4] = odomAftMapped->twist.twist.linear.y;
transformBefMapped[5] = odomAftMapped->twist.twist.linear.z;
}
四、接收laserOdometry的信息
这个回调函数主要是接收到/laser_odom_to_init话题后进行,先根据接收到的数据对相关变量进行赋值操作,然后进入到transformAssociateToMap()函数进行位姿变换融合,最后将融合后的位姿变换发布出去,发布的话题为:
- /integrated_to_init:融合后的当前帧相对于初始帧(世界坐标系)的位姿变换
另外,广播了/camera相对于/camera_init的坐标变换
//接收laserOdometry的信息
void laserOdometryHandler(const nav_msgs::Odometry::ConstPtr& laserOdometry)
{
double roll, pitch, yaw;
geometry_msgs::Quaternion geoQuat = laserOdometry->pose.pose.orientation;
tf::Matrix3x3(tf::Quaternion(geoQuat.z, -geoQuat.x, -geoQuat.y, geoQuat.w)).getRPY(roll, pitch, yaw);
//得到旋转平移矩阵
transformSum[0] = -pitch;
transformSum[1] = -yaw;
transformSum[2] = roll;
transformSum[3] = laserOdometry->pose.pose.position.x;
transformSum[4] = laserOdometry->pose.pose.position.y;
transformSum[5] = laserOdometry->pose.pose.position.z;
transformAssociateToMap();
geoQuat = tf::createQuaternionMsgFromRollPitchYaw
(transformMapped[2], -transformMapped[0], -transformMapped[1]);
laserOdometry2.header.stamp = laserOdometry->header.stamp;
laserOdometry2.pose.pose.orientation.x = -geoQuat.y;
laserOdometry2.pose.pose.orientation.y = -geoQuat.z;
laserOdometry2.pose.pose.orientation.z = geoQuat.x;
laserOdometry2.pose.pose.orientation.w = geoQuat.w;
laserOdometry2.pose.pose.position.x = transformMapped[3];
laserOdometry2.pose.pose.position.y = transformMapped[4];
laserOdometry2.pose.pose.position.z = transformMapped[5];
pubLaserOdometry2Pointer->publish(laserOdometry2);
//发送旋转平移量
laserOdometryTrans2.stamp_ = laserOdometry->header.stamp;
laserOdometryTrans2.setRotation(tf::Quaternion(-geoQuat.y, -geoQuat.z, geoQuat.x, geoQuat.w));
laserOdometryTrans2.setOrigin(tf::Vector3(transformMapped[3], transformMapped[4], transformMapped[5]));
tfBroadcaster2Pointer->sendTransform(laserOdometryTrans2);
}
五、位姿融合
这里的位姿融合部分与laserMapping中的求解地图坐标系中end时刻到初始时刻的初始猜测–transformAssociateToMap()函数完全一致。
1.求解位移增量
"transformBefMapped - transformSum"的含义是上一帧相对于初始帧的位移量 与 当前帧相对于初始帧的位移量 的差值,得到的结果是初始帧init坐标系下的位移增量
t
i
n
i
t
s
t
a
r
t
−
e
n
d
t_{init}^{start-end}
tinitstart−end。
然后将其变换到end时刻:
t
i
n
i
t
s
t
a
r
t
−
e
n
d
=
R
e
n
d
_
i
n
i
t
∗
t
i
n
i
t
s
t
a
r
t
−
e
n
d
=
R
i
n
i
t
_
e
n
d
−
1
∗
t
i
n
i
t
s
t
a
r
t
−
e
n
d
R
i
n
i
t
_
e
n
d
−
1
=
R
Z
X
Y
−
1
=
R
−
r
z
R
−
r
x
R
−
r
y
t_{init}^{start-end} = R_{end\_init} * t_{init}^{start-end} = R_{init\_end}^{-1} * t_{init}^{start-end} \\ R_{init\_end}^{-1} = R_{ZXY}^{-1} = R_{-rz} R_{-rx} R_{-ry}
tinitstart−end=Rend_init∗tinitstart−end=Rinit_end−1∗tinitstart−endRinit_end−1=RZXY−1=R−rzR−rxR−ry
对应于下面代码中所示的变换。
2.求解旋转部分的融合
现在这里的变量含义分别表示为:
- transformSum:laserOdometry模块的当前帧相对于初始帧的变换 R i n i t _ e n d L R_{init\_end}^L Rinit_endL
- transformBefMapped:laserMapping模块的当前帧相对于初始帧的变换 R i n i t _ e n d M R_{init\_end}^M Rinit_endM
- transformAftMapped:laserMapping模块的优化后的当前帧相对于初始帧的变换,也可以理解为当前帧相对于地图坐标系的变换 R m a p _ s t a r t M R_{map\_start}^M Rmap_startM
- transformMapped:融合后的当前帧相对于初始帧的坐标变换 R m a p _ e n d F R_{map\_end}^F Rmap_endF
那么有如下坐标变换关系:
R
m
a
p
_
e
n
d
F
=
R
m
a
p
_
e
n
d
M
∗
R
i
n
i
t
_
e
n
d
M
−
1
∗
R
i
n
i
t
_
e
n
d
L
=
R
Z
X
Y
∗
R
Z
X
Y
−
1
∗
R
Z
X
Y
R_{map\_end}^F = R_{map\_end}^M * R_{init\_end}^{M -1} * R_{init\_end}^L = R_{ZXY} * R_{ZXY}^{-1} * R_{ZXY}
Rmap_endF=Rmap_endM∗Rinit_endM−1∗Rinit_endL=RZXY∗RZXY−1∗RZXY
这里的计算公式与laserOdometry模块中的IMU修正部分完全一样:
R
m
a
p
_
e
n
d
F
=
[
c
a
c
y
c
a
c
z
+
s
a
c
x
s
a
c
y
s
a
c
z
c
a
c
y
s
a
c
z
+
s
a
c
x
s
a
c
y
c
a
c
z
c
a
c
x
s
a
c
y
c
a
c
x
s
a
c
z
c
a
c
x
c
a
c
z
−
s
a
c
x
−
s
a
c
y
c
a
c
z
+
s
a
c
x
c
a
c
y
s
a
c
z
s
a
c
y
s
a
c
z
+
s
a
c
x
c
a
c
y
c
a
c
z
c
a
c
x
c
a
c
y
]
R_{map\_end}^F=\left[ \begin{matrix} cacycacz+sacxsacysacz& cacysacz+sacxsacycacz& cacxsacy\\ cacxsacz& cacxcacz& -sacx\\ -sacycacz+sacxcacysacz& sacysacz+sacxcacycacz& cacxcacy\\ \end{matrix} \right]
Rmap_endF=
cacycacz+sacxsacysaczcacxsacz−sacycacz+sacxcacysaczcacysacz+sacxsacycaczcacxcaczsacysacz+sacxcacycaczcacxsacy−sacxcacxcacy
R
m
a
p
_
e
n
d
M
=
[
c
b
c
y
c
b
c
z
+
s
b
c
x
s
b
c
y
s
b
c
z
c
b
c
y
s
b
c
z
+
s
b
c
x
s
b
c
y
c
b
c
z
c
b
c
x
s
b
c
y
c
b
c
x
s
b
c
z
c
b
c
x
c
b
c
z
−
s
b
c
x
−
s
b
c
y
c
b
c
z
+
s
b
c
x
c
b
c
y
s
b
c
z
s
b
c
y
s
b
c
z
+
s
b
c
x
c
b
c
y
c
b
c
z
c
b
c
x
c
b
c
y
]
R_{map\_end}^M=\left[ \begin{matrix} cbcycbcz+sbcxsbcysbcz& cbcysbcz+sbcxsbcycbcz& cbcxsbcy\\ cbcxsbcz& cbcxcbcz& -sbcx\\ -sbcycbcz+sbcxcbcysbcz& sbcysbcz+sbcxcbcycbcz& cbcxcbcy\\ \end{matrix} \right]
Rmap_endM=
cbcycbcz+sbcxsbcysbczcbcxsbcz−sbcycbcz+sbcxcbcysbczcbcysbcz+sbcxsbcycbczcbcxcbczsbcysbcz+sbcxcbcycbczcbcxsbcy−sbcxcbcxcbcy
R
i
n
i
t
_
e
n
d
M
−
1
=
[
c
b
l
y
c
b
l
z
−
s
b
l
x
s
b
l
y
s
b
l
z
−
c
b
l
x
s
b
l
z
s
b
l
y
c
b
l
z
+
s
b
l
x
c
b
l
y
s
b
l
z
−
c
b
l
y
s
b
l
z
+
s
b
l
x
s
b
l
y
c
b
l
z
c
b
l
x
c
b
l
z
s
b
l
y
s
b
l
z
−
s
b
l
x
c
b
l
y
c
b
l
z
−
c
b
l
x
s
b
l
y
s
b
l
x
c
b
l
x
c
b
l
y
]
R_{init\_end}^{M -1}=\left[ \begin{matrix} cblycblz-sblxsblysblz& -cblxsblz& sblycblz+sblxcblysblz\\ -cblysblz+sblxsblycblz& cblxcblz& sblysblz-sblxcblycblz\\ -cblxsbly& sblx& cblxcbly\\ \end{matrix} \right]
Rinit_endM−1=
cblycblz−sblxsblysblz−cblysblz+sblxsblycblz−cblxsbly−cblxsblzcblxcblzsblxsblycblz+sblxcblysblzsblysblz−sblxcblycblzcblxcbly
R
i
n
i
t
_
e
n
d
L
=
[
c
a
l
y
c
a
l
z
+
s
a
l
x
s
a
l
y
s
a
l
z
c
a
l
y
s
a
l
z
+
s
a
l
x
s
a
l
y
c
a
l
z
c
a
l
x
s
a
l
y
c
a
l
x
s
a
l
z
c
a
l
x
c
a
l
z
−
s
a
l
x
−
s
a
l
y
c
a
l
z
+
s
a
l
x
c
a
l
y
s
a
l
z
s
a
l
y
s
a
l
z
+
s
a
l
x
c
a
l
y
c
a
l
z
c
a
l
x
c
a
l
y
]
R_{init\_end}^L=\left[ \begin{matrix} calycalz+salxsalysalz& calysalz+salxsalycalz& calxsaly\\ calxsalz& calxcalz& -salx\\ -salycalz+salxcalysalz& salysalz+salxcalycalz& calxcaly\\ \end{matrix} \right]
Rinit_endL=
calycalz+salxsalysalzcalxsalz−salycalz+salxcalysalzcalysalz+salxsalycalzcalxcalzsalysalz+salxcalycalzcalxsaly−salxcalxcaly
然后使用对应位置的值相等,就得到了修正后的累计变换acx、acy、acz,计算如下:
a
c
x
=
−
a
r
c
s
i
n
(
R
2
,
3
)
=
−
a
r
c
s
i
n
(
−
s
b
c
x
∗
(
s
a
l
x
∗
s
b
l
x
+
c
a
l
x
∗
c
a
l
y
∗
c
b
l
x
∗
c
b
l
y
+
c
a
l
x
∗
c
b
l
x
∗
s
a
l
y
∗
s
b
l
y
)
−
c
b
c
x
∗
c
b
c
z
∗
(
c
a
l
x
∗
s
a
l
y
∗
(
c
b
l
y
∗
s
b
l
z
−
c
b
l
z
∗
s
b
l
x
∗
s
b
l
y
)
−
c
a
l
x
∗
c
a
l
y
∗
(
s
b
l
y
∗
s
b
l
z
+
c
b
l
y
∗
c
b
l
z
∗
s
b
l
x
)
+
c
b
l
x
∗
c
b
l
z
∗
s
a
l
x
)
−
c
b
c
x
∗
s
b
c
z
∗
(
c
a
l
x
∗
c
a
l
y
∗
(
c
b
l
z
∗
s
b
l
y
−
c
b
l
y
∗
s
b
l
x
∗
s
b
l
z
)
−
c
a
l
x
∗
s
a
l
y
∗
(
c
b
l
y
∗
c
b
l
z
+
s
b
l
x
∗
s
b
l
y
∗
s
b
l
z
)
+
c
b
l
x
∗
s
a
l
x
∗
s
b
l
z
)
)
a
c
y
=
a
r
c
t
a
n
(
R
1
,
3
/
R
3
,
3
)
a
c
z
=
a
r
c
t
a
n
(
R
2
,
1
/
R
2
,
2
)
acx = -arcsin(R_{2,3}) = -arcsin(-sbcx*(salx*sblx + calx*caly*cblx*cbly + calx*cblx*saly*sbly) - cbcx*cbcz*(calx*saly*(cbly*sblz - cblz*sblx*sbly) - calx*caly*(sbly*sblz + cbly*cblz*sblx) + cblx*cblz*salx) - cbcx*sbcz*(calx*caly*(cblz*sbly - cbly*sblx*sblz) - calx*saly*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sblz) ) \\ acy = arctan(R_{1,3}/R_{3,3}) \\ acz = arctan(R_{2,1}/R_{2,2})
acx=−arcsin(R2,3)=−arcsin(−sbcx∗(salx∗sblx+calx∗caly∗cblx∗cbly+calx∗cblx∗saly∗sbly)−cbcx∗cbcz∗(calx∗saly∗(cbly∗sblz−cblz∗sblx∗sbly)−calx∗caly∗(sbly∗sblz+cbly∗cblz∗sblx)+cblx∗cblz∗salx)−cbcx∗sbcz∗(calx∗caly∗(cblz∗sbly−cbly∗sblx∗sblz)−calx∗saly∗(cbly∗cblz+sblx∗sbly∗sblz)+cblx∗salx∗sblz))acy=arctan(R1,3/R3,3)acz=arctan(R2,1/R2,2)
3.将位移增量转换到map坐标系
t
m
a
p
i
n
c
r
e
m
e
n
t
=
R
m
a
p
_
e
n
d
F
∗
t
e
n
d
i
n
c
r
e
m
e
n
t
R
m
a
p
_
e
n
d
F
=
R
Z
X
Y
=
R
y
R
x
R
z
t_{map}^{increment} = R_{map\_end}^F * t_{end}^{increment} \\ R_{map\_end}^F = R_{ZXY} = R_y R_x R_z
tmapincrement=Rmap_endF∗tendincrementRmap_endF=RZXY=RyRxRz
4.求解平移部分的初始猜测
这里注意一点:上面求出来的增量使用的事start时刻的累积位移减去end时刻的累计位移,所以这里在求解时也是减号,如下:
t
m
a
p
_
e
n
d
F
=
t
m
a
p
_
e
n
d
M
+
t
m
a
p
e
n
d
−
s
t
a
r
t
=
t
m
a
p
_
s
t
a
r
t
M
−
t
m
a
p
s
t
a
r
t
−
e
n
d
t_{map\_end}^F = t_{map\_end}^M + t_{map}^{end-start} = t_{map\_start}^M - t_{map}^{start-end}
tmap_endF=tmap_endM+tmapend−start=tmap_startM−tmapstart−end
我在上面声明变量时提到了:地图坐标系map,一定程度上可以理解为里程计第一帧init,这个意思就是可以理解为map坐标系和初始时刻坐标系init以及世界坐标系w是重合的,而laserMapping中虽然写的是变换到了map坐标系,也可以理解为仍然是当前帧end相对于初始帧init的坐标变换,只是经过了laserMapping模块优化,所以这里的 t m a p _ e n d F t_{map\_end}^F tmap_endF也可以写成 t i n i t _ e n d F t_{init\_end}^F tinit_endF,这个解释只是为了符合作者代码中坐标变换时发布的是/camera_init到/camera的变换,所以这里写 t m a p _ e n d F t_{map\_end}^F tmap_endF也没问题。
//odometry的运动估计和mapping矫正量融合之后得到的最终的位姿transformMapped
void transformAssociateToMap()
{
//平移后绕y轴旋转(-transformSum[1])
float x1 = cos(transformSum[1]) * (transformBefMapped[3] - transformSum[3])
- sin(transformSum[1]) * (transformBefMapped[5] - transformSum[5]);
float y1 = transformBefMapped[4] - transformSum[4];
float z1 = sin(transformSum[1]) * (transformBefMapped[3] - transformSum[3])
+ cos(transformSum[1]) * (transformBefMapped[5] - transformSum[5]);
//绕x轴旋转(-transformSum[0])
float x2 = x1;
float y2 = cos(transformSum[0]) * y1 + sin(transformSum[0]) * z1;
float z2 = -sin(transformSum[0]) * y1 + cos(transformSum[0]) * z1;
//绕z轴旋转(-transformSum[2])
transformIncre[3] = cos(transformSum[2]) * x2 + sin(transformSum[2]) * y2;
transformIncre[4] = -sin(transformSum[2]) * x2 + cos(transformSum[2]) * y2;
transformIncre[5] = z2;
float sbcx = sin(transformSum[0]);
float cbcx = cos(transformSum[0]);
float sbcy = sin(transformSum[1]);
float cbcy = cos(transformSum[1]);
float sbcz = sin(transformSum[2]);
float cbcz = cos(transformSum[2]);
float sblx = sin(transformBefMapped[0]);
float cblx = cos(transformBefMapped[0]);
float sbly = sin(transformBefMapped[1]);
float cbly = cos(transformBefMapped[1]);
float sblz = sin(transformBefMapped[2]);
float cblz = cos(transformBefMapped[2]);
float salx = sin(transformAftMapped[0]);
float calx = cos(transformAftMapped[0]);
float saly = sin(transformAftMapped[1]);
float caly = cos(transformAftMapped[1]);
float salz = sin(transformAftMapped[2]);
float calz = cos(transformAftMapped[2]);
float srx = -sbcx*(salx*sblx + calx*cblx*salz*sblz + calx*calz*cblx*cblz)
- cbcx*sbcy*(calx*calz*(cbly*sblz - cblz*sblx*sbly)
- calx*salz*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sbly)
- cbcx*cbcy*(calx*salz*(cblz*sbly - cbly*sblx*sblz)
- calx*calz*(sbly*sblz + cbly*cblz*sblx) + cblx*cbly*salx);
transformMapped[0] = -asin(srx);
float srycrx = sbcx*(cblx*cblz*(caly*salz - calz*salx*saly)
- cblx*sblz*(caly*calz + salx*saly*salz) + calx*saly*sblx)
- cbcx*cbcy*((caly*calz + salx*saly*salz)*(cblz*sbly - cbly*sblx*sblz)
+ (caly*salz - calz*salx*saly)*(sbly*sblz + cbly*cblz*sblx) - calx*cblx*cbly*saly)
+ cbcx*sbcy*((caly*calz + salx*saly*salz)*(cbly*cblz + sblx*sbly*sblz)
+ (caly*salz - calz*salx*saly)*(cbly*sblz - cblz*sblx*sbly) + calx*cblx*saly*sbly);
float crycrx = sbcx*(cblx*sblz*(calz*saly - caly*salx*salz)
- cblx*cblz*(saly*salz + caly*calz*salx) + calx*caly*sblx)
+ cbcx*cbcy*((saly*salz + caly*calz*salx)*(sbly*sblz + cbly*cblz*sblx)
+ (calz*saly - caly*salx*salz)*(cblz*sbly - cbly*sblx*sblz) + calx*caly*cblx*cbly)
- cbcx*sbcy*((saly*salz + caly*calz*salx)*(cbly*sblz - cblz*sblx*sbly)
+ (calz*saly - caly*salx*salz)*(cbly*cblz + sblx*sbly*sblz) - calx*caly*cblx*sbly);
transformMapped[1] = atan2(srycrx / cos(transformMapped[0]),
crycrx / cos(transformMapped[0]));
float srzcrx = (cbcz*sbcy - cbcy*sbcx*sbcz)*(calx*salz*(cblz*sbly - cbly*sblx*sblz)
- calx*calz*(sbly*sblz + cbly*cblz*sblx) + cblx*cbly*salx)
- (cbcy*cbcz + sbcx*sbcy*sbcz)*(calx*calz*(cbly*sblz - cblz*sblx*sbly)
- calx*salz*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sbly)
+ cbcx*sbcz*(salx*sblx + calx*cblx*salz*sblz + calx*calz*cblx*cblz);
float crzcrx = (cbcy*sbcz - cbcz*sbcx*sbcy)*(calx*calz*(cbly*sblz - cblz*sblx*sbly)
- calx*salz*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sbly)
- (sbcy*sbcz + cbcy*cbcz*sbcx)*(calx*salz*(cblz*sbly - cbly*sblx*sblz)
- calx*calz*(sbly*sblz + cbly*cblz*sblx) + cblx*cbly*salx)
+ cbcx*cbcz*(salx*sblx + calx*cblx*salz*sblz + calx*calz*cblx*cblz);
transformMapped[2] = atan2(srzcrx / cos(transformMapped[0]),
crzcrx / cos(transformMapped[0]));
x1 = cos(transformMapped[2]) * transformIncre[3] - sin(transformMapped[2]) * transformIncre[4];
y1 = sin(transformMapped[2]) * transformIncre[3] + cos(transformMapped[2]) * transformIncre[4];
z1 = transformIncre[5];
x2 = x1;
y2 = cos(transformMapped[0]) * y1 - sin(transformMapped[0]) * z1;
z2 = sin(transformMapped[0]) * y1 + cos(transformMapped[0]) * z1;
transformMapped[3] = transformAftMapped[3]
- (cos(transformMapped[1]) * x2 + sin(transformMapped[1]) * z2);
transformMapped[4] = transformAftMapped[4] - y2;
transformMapped[5] = transformAftMapped[5]
- (-sin(transformMapped[1]) * x2 + cos(transformMapped[1]) * z2);
}
总结
到此为止,整个LOAM的讲解就结束了!!
我的感觉就是看LOAM的论文,有一种“作者说的好有道理,确实就是这样啊”的感觉,但是如果要是让自己想,就想不出来这么牛逼的算法,它的代码也写的比较漂亮。
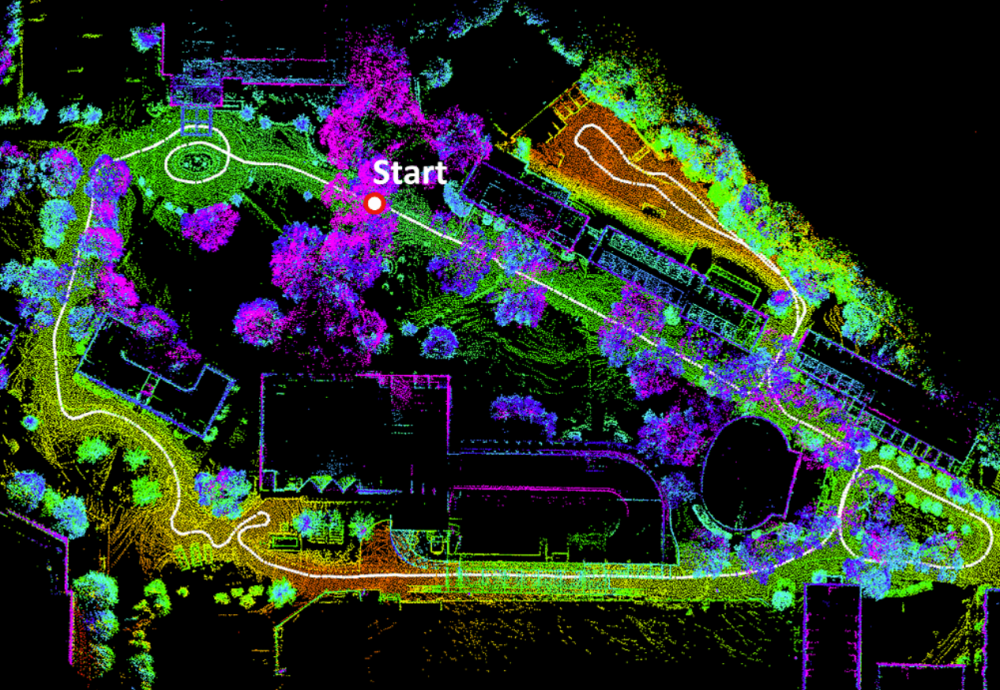
代码的运行就不单独开一篇文章写了,只要装好了依赖,编译很顺畅,也没报什么错,我找了一个数据集测试了一下,也没问题,测试的数据里放在了文章开头提到的我的github仓库的bag文件夹中,运行结果点云图放在了pcl文件夹中,放一张结果截图。文章来源:https://www.toymoban.com/news/detail-665816.html
 文章来源地址https://www.toymoban.com/news/detail-665816.html
文章来源地址https://www.toymoban.com/news/detail-665816.html
到了这里,关于【3D激光SLAM】LOAM源代码解析--transformMaintenance.cpp的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!