174-地下城游戏-Toy模板网

这篇具有很好参考价值的文章主要介绍了174-地下城游戏。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

恶魔们抓住了公主并将她关在了地下城 dungeon 的右下角。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只向右或向下移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

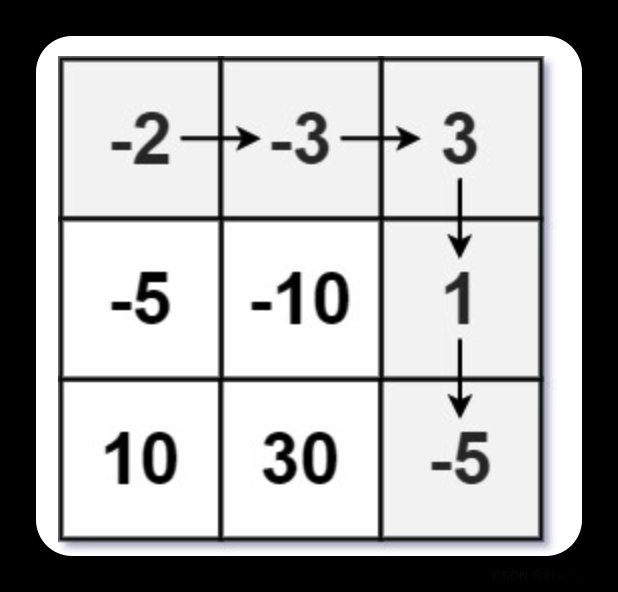
示例 1：
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7 。
示例 2：

输入：dungeon = [[0]]
输出：1
提示：

m == dungeon.length
n == dungeon[i].length
1 <= m, n <= 200
-1000 <= dungeon[i][j] <= 1000

思路

问题描述：地下城由一个m x n的网格组成，骑士从左上角出发，必须通过对抗恶魔来拯救公主，目标是找到骑士进入地下城所需的最低初始健康点数。

解题思路：
这是一个动态规划问题。我们可以从右下角开始逆向考虑，定义 dp[i][j] 为从位置 (i, j) 到达右下角时所需的最低初始健康点数。为了逆向推导，我们从右下角开始向左上角遍历。

对于最后一行和最后一列，只能往右或往下移动，因此需要考虑从当前位置 (i, j) 出发的下一个位置 (i+1, j) 或 (i, j+1)，并且需要保证 dp[i][j] 大于等于1。
对于其他位置，我们需要考虑向右或向下移动，并且选择路径中的最小初始健康点数。因此，dp[i][j] 取决于 (i+1, j) 和 (i, j+1) 中的较小值，且需要保证 dp[i][j] 大于等于1。

最终，初始健康点数应该大于等于 dp[0][0]。文章来源地址https://www.toymoban.com/news/detail-666809.html

代码

object Solution {
  def calculateMinimumHP(dungeon: Array[Array[Int]]): Int = {
    val m = dungeon.length
    val n = dungeon(0).length
    val dp = Array.ofDim[Int](m, n)

    dp(m - 1)(n - 1) = math.max(1, 1 - dungeon(m - 1)(n - 1))
    for (i <- m - 2 to 0 by -1) {
      dp(i)(n - 1) = math.max(1, dp(i + 1)(n - 1) - dungeon(i)(n - 1))
    }
    for (j <- n - 2 to 0 by -1) {
      dp(m - 1)(j) = math.max(1, dp(m - 1)(j + 1) - dungeon(m - 1)(j))
    }

    for (i <- m - 2 to 0 by -1) {
      for (j <- n - 2 to 0 by -1) {
        dp(i)(j) = math.max(1, math.min(dp(i + 1)(j), dp(i)(j + 1)) - dungeon(i)(j))
      }
    }

    dp(0)(0)
  }

  def main(args: Array[String]): Unit = {
    val dungeon1 = Array(Array(-2, -3, 3), Array(-5, -10, 1), Array(10, 30, -5))
    println(calculateMinimumHP(dungeon1))  // 输出 7

    val dungeon2 = Array(Array(0))
    println(calculateMinimumHP(dungeon2))  // 输出 1
  }
}