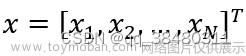长TR,长TE,是T2加权像;
短TR,短TE,是T1加权像;
长TR,短TE,是PD加权像。
一、傅里叶重建
磁共振图像反映的是组织的信号强度。在图像中,如果越白或者越亮,则代表组织的信号强度越高。
磁共振的不同序列反映的是不同组织对比或者叫做不同参数。磁共振图像我们一般把它叫做“加权像”,Weighted Image。
加权或者权重代表突出重点,那种成分占的权重(比例)大。在磁共振成像中,组织所固有的参数特性(T1、T2、PD等)均对磁共振图像的信号强度有所贡献,但是一副磁共振图像,如果反映了各种组织参数在里面,那么就等于没有反映任何指标,因为都是在对图像信号强度做贡献,我们不知道那种贡献大,通过看图像明暗度,不能判断。
所以,磁共振图像,应该重点反映那种组织对图像的贡献最大。一般,我们是通过调整参数,使磁共振图像主要反映组织某一个方面的特性,这样我们就能够进行判读了。另外,我们不可能得到一个纯粹的只反映组织一个特性的磁共振图像。所以,这也是为什么磁共振图像,很多我们会叫做加权像的原因。
常规的磁共振图像主要有以下几种:
T1加权像(T1WI):主要是反映组织之间T1差别的图像,也就是主要反映 组织之间纵向弛豫差别的图像;
T2加权像(T2WI):主要是反映组织之间T2差别的图像,也就是主要 反映组织之间横向弛豫差别的图像;
PD(质子密度)加权像(PDW):主要是反映 组织之间质子密度,也就是氢质子含量差别的图像。
二、填零
填零:若K空间为是按直线轨迹(笛卡尔方格)全采样,2D或3D-IFT要使用的FFT需要输入数据为2的整数次幂,采集的数据通过补零来满足这个条件。
填零导致图像按sinc插补的加采样,在显示矩阵中提供sinc插补像素。填零不增加任何信息含量,不影响SNR,不影响图像的实际分辨率,但填零能给图像信号一个平滑“延申”或降低由“部分体积效应”引起的块状伪影,从而提高图像的表观图像分辨率。
但由于FT长度增加,重建时间增加。对于大矩阵图像数据可能使显示或存档的系统函数卡壳,还可能增大图像中的截断伪影(Gibbs跳动) 的显著性(Gibbs伪影出现的原因是采样不足,或者空间分辨率不够大,或者体素还不够小)。
部分容积效应:CT图像上各个像素的数值代表相应单位组织全体的平均CT值,它不能如实反映该单位内各种组织本身的CT值。
Gibbs伪影又叫截断伪影或者叫环形伪影,跟图像的空间分辨率有关。一副图像是包含了无数个(无限个)空间频率的。但是我们在通过系统采集图像信号的时候,我们只能采样有限数目的频率。简单来讲就是,我们 用有限的数字体素来描述图像。 在图像的高对比度界面,由于图像变化太大,而有限的像素无法描述这种大变化的时候,则会产生一种伪影,我们把这种伪影叫做 截断伪影,或者 环形伪影,也叫 Gibbs伪影,振铃伪影。 根据这种伪影的特点,它一般出现在图像高对比度界面的周围,形成交替的亮带和暗带。这种伪影可以出现在相位编码方向,也可以出现在频率编码方向。但是出现在相位编码方向的概率大。因为,相位编码方向步级决定扫描时间,一般来说,相位编码方向存在采用不足的可能性比频率编码方向大。
三、移相
将序列值输入到FFT时,算法假定DC点(即零频、零时间点)为起始点S0。
MRI数据一般不是按FFT期望的输入次序采集和储存的。当应用FFT到K空间数据时,需要调整数据列次序以适合FFT的要求,普遍情况是存储数据以DC点位于K空间中点,而在FFT后进行相位校正以补偿N/2位移。
FFT算法假定输入、输出数据相对于传统次序移动了N/2。这种移动是 在傅里叶共轭域一个符号交替实现的。符号交替输入给输出移动。对于模重建,FT之后符号交替步可以跳动,但FT之前必须进行符号交替。
MRI数据不是按FFT期望的输入次序采集和储存的,当应用FFT到K空间数据时,这数据要调整次序以适合FFT的要求。普遍情况是储存数据 以DC点位于Kx、Ky、Kz方向的中点(假定全K空间采样),而在FFT之后进行相位校正以补偿N/2位移。类似的,FFT算法的输出数据序列是以DC值作为起点而不是在中心,这就需要更正次序,移动DC点回到中心(在FFT之前加一个位移就可以自动完成)。
四、数据窗函数
截断伪影:当测量数据只包含磁化强度傅里叶分量完全数据的低频子集时,这种重建的图像包含上冲和跳动伪影(特别是靠近锐变的边缘处)。
切趾:把K空间数据乘以一个能平滑衰减高空间频率的滤波器或窗函数,就能降低跳动伪影。
1D Tukey窗:适用于MRI的K空间数据的一个窗函数的例子是余弦锥型或Turkey窗,此窗给出的点扩散函数的空间分辨率是各向异性的,即在图像中随方向而变。 
不可分割的窗:一个普通的函数时用具有与方向角无关的各向同等截止点Kc的窗,给出各向同性空间分辨率。
任何磁共振图像,都存在Gibbs伪影。如果图像的采样点非常大,那么产生的Gibbs伪影的条纹就近似于无限薄,条纹之间距离近似于无限接近,也就没有伪影了。首要的方法是:减小体素,提高空间分辨率,提高采样,因为提高分辨率,会增加扫描时间,故不采用这种做法。在飞利浦系统中,可以把环形过滤Ringing Filter打开,这样会尽量消除这个伪影。
点扩展函数(point spread function PSF)描述了成像系统对点源或点对象的响应。点目标的扩散/模糊程度是衡量成像系统质量的一个指标。一个复杂对象的像可以被看作是真实对象和PSF的卷积。然而,当被检测到的光是相干的(coherent),图像在复数域( complex field)的形成是线性的。记录灰度图(intensity image),然后可以引发 cancellations 或其他非线性效应。
五、矩形视野
很多解剖截面可用椭圆来近似,即矩形视野,由于ADC采样速度足够高,安排频率编码在长FOV方向而相位编码在短FOV方向
为避免读出方向混叠伪影,可采用过采样技术;要避免相位编码方向的混叠,可采用空间预饱和。
一般有三种方式执行傅里叶变换:
1、离散傅里叶变换(DFT)。但DFT比FFT慢。
2、K空间内插对于相位编码数据维给出2的整数次幂,然后用FFT。物体是紧支的,sinc内插费时,更快的方法是 方格化。从K空间数据方格化再取样产生混叠,有时造成图像质量损失。
3、相位编码数据维通过填零给出2的整数次幂,然后用FFT,并在图像空间内插以恢复正确的比例。
奈奎斯特频率定义为信号带宽的两倍。如果实际采样频率高于奈奎斯特频率,即为过采样。低于奈奎斯特采样频率进行采样就称为欠采样。过采样能够提高分辨率和信噪比SNR,并且通过放宽抗混叠滤波器的性能要求,有助于避免混叠和相位失真。
部分容积效应:CT图像上各个像素的数值代表相应单位组织全体的平均CT值,它不能如实反映该单位内各种组织本身的CT值。
空间预饱和脉冲用于抑制来自成像视野内解剖区域的不良信号。尽管在大脑成像中并不常用,但可用于抑制来自邻近血管的信号,从而最大程度地减少了重影伪影。
六、多线圈数据重建
当多线圈多接受通道采集数据时,各线圈通道的复数像分别单独重建,然后用其平方和的平方根计算出最终图像。如果各线圈的图像是Ij(x,y)(j是线圈编号),则最终的2D图像是:
由平方和近似造成的SNR损失只有百分之几,通过用下式近似这个接受线圈B1场:
七、图像变形校正
通过折中线性度、减少高度线性区的体积,可达到更高的梯度幅度和斜升率,这样的折中对很多不需要大体积的应用如脑fMRI很有吸引力。因距磁体距离的不同而造成的图像在尺寸和强度上变形,可根据梯度场设计数据或测量数据可以进行校正。而其他由梯度非线性造成的变形一般都由及其自动校正。

不同评价指标(即特征向量中的不同特征就是所述的不同评价指标)往往具有不同的量纲和量纲单位,这样的情况会影响到数据分析的结果。为了消除指标之间的量纲影响,需要进行数据标准化处理,以解决数据指标之间的可比性。原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价。其中,最典型的就是数据的归一化处理。
简而言之,归一化的目的就是使得预处理的数据被限定在一定的范围内(比如[0,1]或者[-1,1]),从而消除奇异样本数据导致的不良影响。
奇异样本数据 是指相对于其他输入样本特别大或特别小的样本矢量(即特征向量)。奇异样本数据的存在会引起训练时间增大,同时也可能导致无法收敛,因此,当存在奇异样本数据时,在进行训练之前需要对预处理数据进行归一化;反之,不存在奇异样本数据时,则可以不进行归一化。
(1)归一化后加快了梯度下降求最优解的速度,也即加快训练网络的收敛性;
(2)归一化有可能提高精度。
八、缩放比例
MRI信噪比正比于像素体积,也正比于总采集时间(正比于K空间中Kx、Ky、Kz方向采样点数Nx、Ny、Nz及激发次数Nex)的平方根,由下式表示:
对于某些接收机硬件,一个DC偏移可能出现在测量的K空间数据中。RF激发脉冲的相位循环可以消除基线;也可以在数据采集采集的开始或结束时测量基线,然后从原始数据中减掉。
九、基线校准
测量基线是在不加梯度和RF的情况下采集数据。选择测量时间给出基线估计(可忽略噪声)。也可以不采集额外的数据,而是在K空间中(FID或回波)对最后几个点取平均来估计基线。一个关键的假定是磁化强度在K空间行的末尾已经衰减或散相,剩余的信号相应到DC偏移。 文章来源:https://www.toymoban.com/news/detail-666916.html
文章来源:https://www.toymoban.com/news/detail-666916.html
DC是Deflection Coefficient的缩写,是偏因径系数;DC偏移是指由于输入设备的某些问题,导致电流波形偏移了中轴线走向X或者Y方而产生的现象。文章来源地址https://www.toymoban.com/news/detail-666916.html
到了这里,关于【核磁共振成像】傅里叶重建的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!