乘积最大子数组文章来源:https://www.toymoban.com/news/detail-667493.html
思路:
看到这个题的时候 要用DP的想法去做这道题
想到遍历到前面的值能不能为后面所用
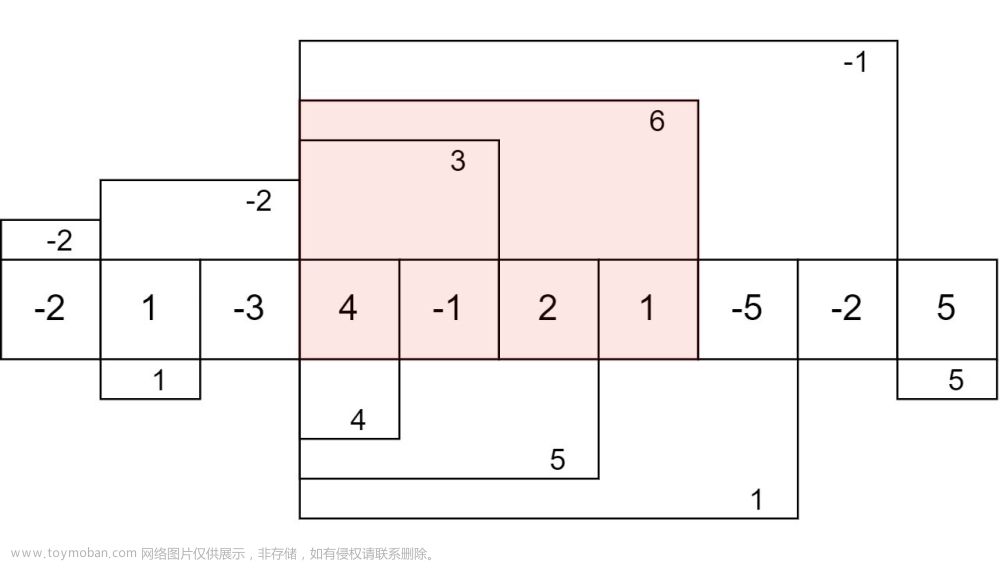
假设有n个值 我们可以记录一下 第i个值的最大值是什么 怎么用到前面的值取判断
第i个值 可能正数 也可能是负数
如果是正数 那么我们乘以后面第i-1位的最大值 可以得到当前位置的最大值
如果是负数 那么我们乘以后面第i-1位的最小值 可以得到当前位置的最大值
那么当前位置最小值怎么得到 同最大值一样
需要f g分别表示前1位置的最大值和最小值 用a来表示当前位置的值 那么最大值肯定在fa ga 或者a
这三个值中得到 最小值也是
代码如下文章来源地址https://www.toymoban.com/news/detail-667493.html
class Solution {
public:
int maxProduct(vector<int>& nums) {
//记录一下最终的结果 把第一位传入
int res =nums[0];
int f =nums[0], g = nums[0];
//从下标1开始遍历
for(int i = 1 ;i < nums.size() ;i++)
{
//a为当前值 fa表示最大值和当前值的乘积 ga表示最小值和当前值的乘积
int a= nums[i],fa=f *a ,ga =g*a;
//最大值在a fa ga 三个值中决定
f= max(a,max(fa,ga));
g = min(a ,min(fa,ga));
//总结果的最大值在res 和f(当前位置的最大值决定)
res = max(res ,f);
}
return res;
}
};
到了这里,关于乘积最大子数组--动态规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!