线性代数的本质笔记（3B1B课程）

前言

最近在复习线代，李永乐的基础课我刷了一下，感觉讲的不够透彻，和我当年学线代的感觉一样，就是不够形象。

比如，行列式为什么那么重要，它的含义究竟是什么？特征值到底代表了什么？等等。说白了，我需要几何直观的理解。

几何直观解决的问题是，我为什么要用这个，有什么用，而数值计算只是让我们能应用罢了，可惜我们只是学了数值计算。

于是我开始刷3b1b的《线性代数的本质》

这篇文章是观看视频后我的个人感悟，可以结合视频一起食用，有解释的不清楚的地方，以视频为准，毕竟我理解的还是不够深入

线性代数的本质

向量

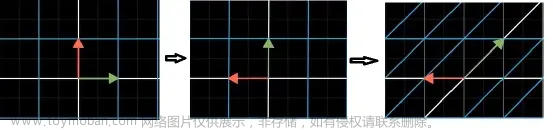
在线性代数中，向量是以原点为起点的箭头，终点坐标和向量的值是一样的。

因此，向量之间的空间上的运算也可以变成向量值的运算，比如向量和（移动），向量数乘（缩放）。

之所以能够用向量对应向量值，是因为有一个i和j的基底。说白了，就是坐标系。如果基底变了，要保持向量不变的话，向量值就要改变。

总之，用数值（向量值）描述向量，要依赖于基底。

如果两个基底不共线（线性无关），则可以张成一个面，否则只能是一条线

如果是三个线性无关的向量，则可以张成一个三维空间，如果是n个线性无关的向量，则可以张成n维空间，但是这个就是无法想象的了。

如何理解线性相关呢？所谓线性相关，就是说某一个向量落在了其他向量张成的空间内，不需要这个向量了，可以移除这个向量而不影响向量组张成的空间。

假设给定3个向量的向量组，假设两个向量共线，那么必然线性相关（充分条件），但是如果三个向量都不共线，就能说明线性无关了吗？不能。

下面4条等价：

1. 线性相关
2. 有一个向量落在其他两个向量张成的平面内
3. 该向量可以被其他向量线性表出
4. 存在不全为0的k，使得
   $k_1{\alpha }_1+\cdots +k_n{\alpha }_n=0$

前面的都好理解，第4条可以这么理解，基于3，可以得到第i个向量=其他向量的线性组合，那么令$k_i=-1$，不就是一组不全为0的系数，让这个向量组的计算结果=0吗？

矩阵

矩阵有两种含义

1. 向量组
2. 对向量的线性变换

给定一个向量，乘一个矩阵，就可以变成新向量，这就是矩阵的几何意义。

当一个矩阵里面的所有向量被同时变换，那就是矩阵的线性变换。

但是无论是向量，还是矩阵，其变换都是通过乘以矩阵实现的。

实际上任何函数都可以变换空间，只是线性变换后，曾经的直线还是直线，原点也没有变化。本质在于，线性变换是均匀的，保持网格线平行且等距均匀分布的变换。

用另一个说法去说，就是基底是线性变换的，而曾经的所有向量与基底的关系保持不变，变的，只是向量本身的值，而不是向量和基底的关系。

所以考虑线性变换，我们其实只需要记住两个事情：

1. 原始向量和原始基底的关系，这个关系会保持不变
2. 基底的情况，这会随着线性变换而变

这两点注意好，无论你怎么变基底，都可以迅速推断出新向量的位置

实际上，对于二维来说，一个向量本身就是$(\hat{i},\hat{j})\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]=k_1\hat{i}+k_2\hat{j}$

而$(\hat{i},\hat{j})$本身就是一个矩阵,$\left[\begin{array}{c}10\\ 01\end{array}\right]$

可以直观地理解：

1. 左边的矩阵，从左到右是n个基底
2. 右边的向量代表向量和基底的关系，就是线性标出的系数
3. 新的向量就是新的基底的线性组合，最后算出来的值，就是新的基底下，向量的值。
   • 新向量按照维度理解，则每一个维度，都是基底按照系数线性组合的结果

进一步总结：任何一个向量都等于基底乘以系数向量，包括最开始的i，j基底。

通过这个思路，就可以理解，旋转和剪切是如何实现的了。

如果新的基底在一条直线上，那么原有的二维空间就会被挤压到一维空间上，这就是降维了。

进一步理解矩阵和矩阵相乘。

如果说一个矩阵描述了新基底，那么另一个矩阵就是把基底再进行一次变换，两次基底的变换可以复合成一次性的线性变换。

所以矩阵乘，有两种理解：

1. 把一个空间的每一个向量都变成新的向量，形成新的空间
2. 把两个线性变换复合为一个线性变换

按照这个思路去理解，只要不影响从右到左的变换顺序，那么就不影响最终结果，所以矩阵乘具有结合和分配，但是没有交换运算。

行列式

因为是线性变换，所以对于基底向量构成的方格的面积变换，这个比例对于任何方格都是一样的。

即使一个形状不是方格，也可以用方格近似，所以任意面积，在经过线性变换以后，变换的比例是恒定的。

这个面积变换的比例，就是行列式。

为什么存在线性相关向量的矩阵，行列式=0呢？就是因为降维了，导致体积被压缩为0.1

当然，行列式也是有可能出现负值的，那代表什么呢？对于二维空间来说就是翻了个面，学术点就是改变了空间的定向，所谓定向，就是基底的相对位置（比如二维中，正定向是i永远在j左边，三维中，符合右手定则）

为什么把行列式的两行/两列交换后取值要加负号呢？就是因为交换会改变定向，相当于翻了个面。

具体要问行列式怎么计算，下图是二维情况。当然，这就是图一乐，实际上你不会这么去算的，就是理解一下，确实是面积的放大比例。

线性方程

我们先讨论非齐次线性方程。

其几何意义在于，寻找一个线性组合x，让这个向量经过基底A变换后，与v对齐

当然，这种情况是复杂的，线性变换后到底降没降维，可以用秩来描述。秩就是A张成的列空间的维度

如果r（A）<n，就代表降维了，自然det（A）=0

如果A的行列式不为0，也就是说A张成的空间可以把v覆盖，那么就有且只有一个x在变换后能和v重合。

这就是唯一解的条件：r（A）=n（或者行列式≠0），代表满秩，r（A,v）=r（A），代表A可以线性表出v。其实后一个条件压根没必要，只要满秩，A的空间维度一定可以覆盖v。

而且，因为是唯一解，具有一一映射的特性，所以可以通过逆映射，即一个逆向线性变换把v倒回x，这就是逆矩阵。

如果行列式=0，即r（A）< n，那么正向变换是降维的，也就是说会把空间压缩，但是你要知道，v是没有被压缩的，还是高维的，那么就有两种可能：

1. v恰好落在降维后空间内，即v可以被A线性表出，即r（A）=r（A，b）
2. v落在降维后空间外，即r（A）< r（A，b），此刻无解

如果在降维后，还有解的话，那么v这个位置其实是被压缩了无数个向量的

这不是一一映射，你自然无法把一条线逆向变回一个平面，所以det（A）=0时，没有逆矩阵。

从空间角度理解可逆变换的几何意义，就是不降维的变换。

非齐次说完了，说一下齐次吧。

其次就是v=0的特殊情况，0向量，无论被如何压缩，都可以落在空间之中，所以一定有解。

那么有一个解，还是无穷解，就取决于空间是否被压缩了，比如下面这条线被压缩为一个点的时候，无数个非零向量都被压缩为了0向量。

这就是齐次方程无穷非零解的情况，降维必无穷非零。

我们再来思考一下基础解系。你有想过为什么基础解系基底的数量是n-r（A）个吗？

以三维举例，如果只压缩1个维度，那么从空间上来说，就是沿着一条线把一个三维空间压扁。因此，只压缩一个维度，就会有一条线上的所有向量压缩为0向量，此时只需要1个基底就可以表示所有线性变换前的向量（解）

如果压缩2个维度呢？从空间来想象，就是沿着一个面的方向，把三维空间收缩成一束，想象一下你用拇指和食指套成一个圈儿，把很多线捏成一束的过程。

既然是沿着面，那么这整个面上的向量就都会被压缩为0向量，此时就需要用2个基底去表示这一个面上的解向量了。

最后，因为基础解系张成的子空间比较特殊，专门给起了个名字叫矩阵的“零空间”，或者“核”，还是比较形象的，压缩以后只剩一个点了，压缩前那不就是核心嘛。

基础解系就是零空间的基底。

非方阵

方阵代表同一个维度的空间之间的线性变换（不考虑降维情况）

如果是非方阵，就要考虑m和n了。n列代表输入空间是n维的，m代表输出空间是m维的。

什么意思呢？比如在二维空间中，向量在一个平面上，经过了3×2矩阵，变成了3维向量后，向量存在于空间。

然而这并不代表这个升维后的向量，就能脱离原有的平面，非方阵只是把原有平面抬升到更高维的空间，但是平面还是平面，只是倾斜了，正如一张纸上的线，放到空间中，还是一条线。

说白了，m＞n的情况下，矩阵只是把原来n个低维基底，转移到了高维的空间中，基底仍然是n个

如果是2×3矩阵呢？代表了把3维空间压缩到2维空间，这个变换是很不舒服的，因为把3个基底放到了2维空间，很明显有一个基底就是冗余的了。

二维也可以压缩到一维，根据线性性质，平面上等距的点，压缩成数后，仍然等距。

个人补充：秩与空间维度

矩阵的秩，r（A），这个东西经常在线代中出现

给定n个向量，为什么r（A）<n就等价于线性相关？都可以用秩和维度来解释

秩的几何意义

秩的几何意义即基底张成的线性空间的维度

比如给你两个线性无关的向量，那么秩一定是2，两个向量可以张成平面，n个线性无关的向量，则秩为n，空间维度也是n

用空间维度视角看，可以解释特别多的公式：

给定n个向量，如果β可以被这n个向量线性表出，那么r（A，β）和r（A）就相等，为何？

仔细回想两个向量作为基底的情况，其线性表出的向量一定是在这个平面之中的，也就是说无论如何都逃不出基底张成的空间，既然逃不出，那么有没有这个新表示出的向量，都不会影响原有空间的维度

当把这个思路用秩描述出来，就是r（A，β）=r（A），加不加β都不影响原有空间的维度（秩）

那么按这个视角，线性相关的定理其实也很简单：

给定n个向量，n个向量总共的秩小于n，则线性相关

这是因为，秩＜n，代表空间维度顶天也就n-1。而我们前面说了，每多一个线性无关的向量，张成的空间维度就要+1，顶天n-1维，那么最多n-1个线性无关向量，至少有一个向量是落在原有n-1个向量张成的空间内的，换句话说，这个向量可以被剩余n-1个向量线性表出，这不就是线性相关吗？

秩的决定因素

秩的意义就在于维度，那么线性空间的维度到底受什么影响呢？是m，还是n？

实际上，r（A）≤min（m，n），你想过为什么吗？

先说一下m和n代表什么。m代表一个向量里有几个分量，而n代表线性空间的基底数量。

我们放一个例子

首先是m＞n的，此时每个向量用3个分量表示，分别是xyz，第一反应是这个空间一定是三维的吧。其实不然。

分量的数量（m），只能决定空间维度的上限，比如说你用xyz，不可能描述出4维空间，但是可以写出一个平面方程，即空间的维度数不能突破分量的上限

也就是r（A）<m

再来看n。n代表基底，张成的空间维度不可能超过基底数量。因此可以看下图，虽然整个大空间是3维，但是我现在只有两个基底，我也只能张成一个二维平面，只不过二维平面是放在了三维空间中，是倾斜的。

也就是r（A）<n

总的来说，其实就是m决定了整个空间的维度上限，无法突破。然后在m的限制下，给定n个基底，我们可以去张一个空间出来，有几个线性无关向量，则空间维度就是多少。

秩的计算原理

说了这么多，如何计算出空间的维度呢？

我们一开始学矩阵，就学了这个方法：化简为阶梯型，阶梯型中非0的行数就是秩

我们看维度，根本是看线性无关，而0行的所有列都是0，是否线性无关是不影响的，所以我们完全可以忽略0行。

只看非零行，关键在于主元。化为阶梯型后，主元所在的列，一定是线性无关的，[0,1]和[2,0]，这两个列向量一定是线性无关的。那么非主元列呢，一定可以被主元列表示出来，也就是说这几列是可有可无的。

换句话说，如果主元有k个，那么r（A）=k

最后再收网，主元个数=非零行数，因此r（A）=非零行数

这就是为什么这套流程能算出秩的原因了，这套理解打通了从主元到秩，到空间维度的整个链条，主元可以说是联系了行和列的关键。包括后面理解基础解系的时候，其实也都可以沿用这个思路，就是这么自信。

毕竟，怎么会有本质解释不了现象呢？

个人补充：行列式的本质与发散

​“三行四列行列式怎么算？”

我们都知道三行四列行列式不能算，但是似乎只是因为规定不能算而不能算​，而没有思考过为什么三行四列行列式没意义。

​首先要明白行列式的几何意义：线性变换导致的空间尺寸变化倍数。

如果det=2，那么假设原来空间里有一个方块，变换后的平行四边形面积就是原来的二倍，带负号则代表空间翻了个面（定向改变）

然后你就会明白，当矩阵变换导致空间降维的时候，面积倍数肯定是0，比如你把平面压成线，面积必然是0，因此

降维等价于det（A）=0

而降维实际上代表着线性变换矩阵里面的向量不足以撑起对应维度，也就是线性相关，因此才有

线性相关等价于det（A）=0

而你都降维了，自然不可能还原回去，就好比你可以把人照成纸片人，但是给你一个纸片人，你是无法把他变成人的，因此

det=0又等价于矩阵不可逆

我们这些讨论都是方阵，方阵分为降维和不降维的情况，自然有讨论的必要，而非方阵必然有维度变化，自然没有用行列式的必要。

这里说的维度是指整个空间的维度，而不是基底张成的线性空间的维度，比如下面这个图，虽然是平面，但是实际在三维空间，那么他的尺寸度量实际上就是0，空间整体的度量都变了，讨论尺寸变化倍数又有什么意义呢？

因此回收开头，你问我三行四列行列式怎么算，我要反问你一句，算出来又有什么意义？

点积

这一节比较难，我上来没听懂，关键在于那个对偶性，对偶性容易和对称混淆，其实完全没关系，要是我说的话，对偶性就是一种一一映射，是唯一的等价关系。

点积的计算公式是把对应的坐标相乘，并把结果相加。另一种计算方法是，把一个向量投影到另一个向量上，模之积就是点积。这两个计算方法看起来毫无关系，他们的联系是什么呢？

记住，我们的目标是发现点积，线性变换，投影的联系，现在讲引理。

我们前面说，线性变换可以把线性的空间变成线性的空间。

那么反过来，只要是把线性空间变成另一个线性空间，就一定有一个，且只有一个唯一的线性变换与之对应。

注意这个唯一性，即使是把二维空间压缩为数轴，不同的压缩方法，其放缩倍数都是不一样的，所以是新的线性空间对应唯一的线性变换。

引理说完了，先来寻找一下和单位向量点积是如何与投影联系起来的。

首先，投影是一个线性变换。把二维空间的向量，投影到一条直线上，很明显这是个线性过程，而且还是二维到一维的。

根据对偶性，只要是线性变换，就一定有一个1×2的矩阵与之对应，即投影矩阵。

投影矩阵到底是多少呢？按照线性变换的几何意义，我们只需要找到i，j两个向量在目标直线上的位置，也就是他们的值就行。

此时引入一个单位向量$\hat{u}$，根据对称性，i在直线上的投影值（新基底），恰好等于u的x轴

这样，我们就用线性变换表示出了投影运算，这是几何上的联系。

从数值上来看，向量通过投影矩阵进行线性变换，投影到单位向量所在直线上的值，恰好等于向量和单位向量的点积。

投影——（几何）——线性变换——（数值）——点积

整个对于单位向量，证明思路就是这样。

非单位向量呢？

非单位向量只是单位向量的放缩，计算点积的结果仍然是数，整个过程仍然是从二维到一维，所以仍然对应一个投影矩阵。

只不过因为投影后基底要放缩，所以投影矩阵整体是要比单位向量情况放缩k倍的，这个矩阵可以理解为先投影，再缩放（乘以向量的模）。

至于点积和线性变换，仍然是数值上的联系。如此，投影和点积就彻底联系起来了。

总的来说，这个证明过程用到了线性变换与矩阵的唯一对应性，也就是对偶性。

对于n维变1维的情况，必然有一个n×1的矩阵可以表示这个线性变换，把这个矩阵转置成向量，我们也可以说，任意一个n维变1维的线性变换，一定有一个空间中的向量v与之相关，这就是点积和线性变换的等价性。

叉积

叉积结果的模，平行四边形的面积。

行列式的几何意义，恰好也是线性变换的放大倍数，就用叉积的两个向量当线性变换，计算行列式就等于叉积结果。

当然最后要定向，分正负。

实际上，叉积是一个向量，垂直于底面，模是底面积。叉积可以说是一个代表底面大小和方向的向量。

具体如何计算叉积呢？就是用行列式， 好啦，问题来了，行列式怎么和叉积的几何意义联系起来的呢？还是对偶性。

一个线性变换，可以等价于和对偶向量的点乘。

整体的计划如下：

1. 首先通过v和w构造线性变换
2. 然后求出对偶向量，这个对偶向量恰好就是叉积
3. 而且这个求对偶向量的过程，恰好也就是通过行列式计算叉积的过程。

这是一个输入向量，输出值的函数，行列式计算结果代表平行六面体的体积，很明显这是个线性变换（行列式的特点就是这样）。

根据对偶性，自然有一个1×3的线性变换，进而根据可以变成和3维向量点积，这个三维向量恰好就是我们要的点积。

之所以叉积要用ijk去代替xyz，写成行列式的样子，其实原理就在于此，ijk只是告诉你，算完以后的p是一个向量。

我们到这里只是给出了p的公式，还没有解释为啥p的模就等于底面积。

还得从最开始，平行六面体的体积来看。设（x，y，z）向量为a。则V=底面积×高=a在p上的投影×p的模

你要注意，高=a在p上的投影，所以底面积就自然等于p的模了。

基变换

不同的坐标系（基底），对于同一个向量，其向量坐标值都是不一样的。

比如，在b1，b2这个坐标系中（称b空间），我们的向量坐标是$[-1,2{]}^T$，但是在原始的i，j坐标系中（称ij空间），向量坐标应该是$[-4,1{]}^T$

如何实现不同基底下，向量的变换呢？

其实就是线性变换。对$[-1,2{]}^T$这个向量应用线性变换，就可以得到线性变换后的坐标值。

怎么去理解这个线性变换的过程呢？这里就有一个矛盾的点：

1. 线性变换的含义是把我们这个ij空间变成b空间
2. 线性变换的实际作用是吧b空间里的向量坐标转换为ij空间的向量坐标

根本问题在于这里对线性变换产生了误解。

我们以前的线性变换，是给定ij空间下的向量，然后作用一个线性变换，变成b空间的向量。

现在呢？我们给的是b空间的向量，压根就不是ij空间的向量，所以这个线性变换起到的并不是线性变换的作用，只是把本应属于b空间但是被误以为在ij空间的向量，从ij空间变换到了b空间。

所以上面那两种解释，其实只是两种不同的理解：

1. 给定ij空间向量，矩阵乘后，将其投射到b空间中，得到的是拉伸后的ij空间坐标
2. 给定b空间向量，矩阵乘后，得到其实际在ij空间的坐标

无论用哪种理解方式，得到的结果都是b空间向量用ij空间基底表示出的坐标。

理解了正向过程，反过来也就好说了，把ij空间真正的向量坐标，再转化为b空间基底表示的向量坐标。

在不同基底下的坐标转换，理解了以后，来看一下对不同坐标进行线性变换应该怎么做。

首先你要明白，我们前面的矩阵，都是对ij空间的线性变换，如果要对非ij空间进行线性变换，是无法直接用矩阵的，人家的基向量就不是ij，我们的矩阵无法直接作用到人家的基向量上。

那么思路就应该是：

1. 先把非ij空间变成ij空间
2. 然后进行线性变换
3. 再把ij空间还原为非ij空间

中间的M是任意的，针对ij空间的线性变换，左右两边只是负责基变换转换视角的。

特征向量与特征值

在线性变换中，大部分的向量，方向都偏离了原有的方向。

有一部分向量，方向不变，这个方向上的所有向量方向都不变，仅仅是被拉伸了，而且倍数是相同的。

这些向量都是特征向量，倍数就是特征值。

这种直线，不止有一条，每一条上都有上面这种特殊的性质，也就是说，一个线性变换的特征值可能有好几个。

这玩意有啥用呢？对特征向量来说，就把一个线性变换简化成伸缩，这就是其意义。

在实际生产中，特征向量也有用，比如给你一个3D旋转变换，矩阵是非常麻烦的，但是你可以找到特征向量，特征向量那条线恰好就是转轴，而且特征值=1.

在数学理论中，特征向量可以用来从另一个角度理解线性变换。之前，我们是把ij变换到新的基底，实现空间的变换，在这个过程中，ij可能旋转，拉伸，比较复杂。

实际上，特征向量的数量和基底数量是一样的，那么我们不去看基底，我们把特征向量拉伸${\lambda }_i$倍，也可以让空间变成我们目标的空间，这样理解就脱离了坐标轴，还原了线性变换的本质。

特征向量的性质讨论完了，该说说怎么算了。

下面这个等式，刚开始学比较懵逼，现在理解起来就很直观了，就是把线性变换简化成拉伸了呗。

把等式变换一下，就可以得到一个线性齐次方程。要有非零解，就一定要降维，所以行列式就等于0。

实际上，如果你把$\lambda$看做变量，你在调整这个值的时候，行列式的几何意义（面积），也在连续变化，当这个变量使得面积=0的时候，这个变量就是特征值。当然，这并不是单调的，所以有多个零点，n阶矩阵最多有n个特征值

有时候，n阶矩阵的特征值小于n个（考虑重根），那就一定有一些特征值算出了虚数。比如下面这个旋转变换，压根就没特征值，所以最后算出俩虚数。

另一种特殊情况是，剪切，特征向量恰好在基向量方向上。这样的结果就是，你会丢失一个特征值，重根对应的特征向量会分布在基向量方向上。

还有一种特殊情况，就是空间整体的拉伸，你把特征值带进去以后，左边的矩阵会变成0矩阵，那么任意向量就都是特征向量了。

最后来说一下对角矩阵，对角矩阵的几何意义是把对应方向上的基向量放大k倍，所以n个对角矩阵相乘其实就是放大$k^n$倍。

除去那些堆特殊情况，大部分情况其实是n阶矩阵有n个特征值，那么如果用这n个特征向量作为新的基底，就是所谓的“特征基”。

用这个基底有个好处，就是复杂的线性变换可以被看做是单纯的基向量放大，所有向量仅仅是伸缩，没有旋转。

那如何用现有基底，去表示特征基下的伸缩变换呢？回顾上一节的基变换，我们先把特征基变成现有基底，然后应用伸缩，再变回特征基。

至于基变换矩阵怎么求，就是把特征基对应特征值排列起来构成矩阵，这也是我们线代里的基本做法。

为什么说这个矩阵就是基变换矩阵呢？有了这个矩阵，每个在特征基空间内的基，比如（1,0,0），经过特征矩阵变换后，就可以得到ij空间内的特征向量坐标，符合基变换的特征，所以我们这么构造是合理的。

其实这就是相似对角化，而相似对角化的条件，其实就等价于你有n个特征基。

抽象向量空间

通过基变换你可以发现，线性代数中的各种运算，其实和基坐标没有什么关系，无论你选什么基底，他们的运算都具有线性性质，我们那些规则也都适用：

线性性质：

1. 可加性：先加在变换=先变换再加
2. 成比例：先乘再变换=先变换再乘

我们前面描述的，二维情况下网格线密度均匀，那只是一种特例，真正的线性性质应该是上面这两条。

实际上，无论是向量，还是函数，还是什么过程，比如求导，微分，只要你是某种转换，而且具有线性性质，那么就可以给它找一组基，写成向量的形式，就可以应用线代的公式和特性。

以多项式举例，选择x的不同幂为基底，则构成了一个向量空间，每个基都是一个向量，只不过我们写成一个函数。

那么给一个多项式，就可以用向量坐标表示出来其在向量空间的位置了。

求导运算是线性变换，所以可以用矩阵表示。

在数学中，除了求导，还有更多的东西是线性变换，凡是线性变换，都可以写成基，矩阵，向量，并且应用线代计算法则。

发明线代的数学家，为了把这种规则推广到各个领域，就需要建立其他领域到线代领域的桥梁，即线性空间的判定。

向量是什么形式并不重要，只要你构造的向量空间只要满足8条公理，就证明这个写法是线性的，可以应用所有线代法则。

之所以我们讲的那么难，就是为了普适，但是普适的代价就是抽象，所以如果真的想学好，其实应该先从具象入手，然后推广到抽象，只是这样就费时间了，所以很矛盾，但是我仍然建议两者互为补充。

文章来源地址https://www.toymoban.com/news/detail-667904.html

到了这里，关于线性代数的本质笔记（3B1B课程）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！