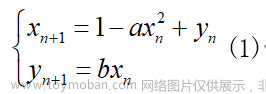目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览




2.算法运行软件版本
matlab2022a
3.部分核心程序
.....................................................................................
lows = 28;
[t1,XX] = ode45(@func_lorenz2,[0 100],[0 1 1.05]);%use the function of ode45 to solve the function
RR1 = XX;
lows = 28.05;
[t1,XX] = ode45(@func_lorenz2,[0 100],[0 1 1.05]);%use the function of ode45 to solve the function
RR2 = XX;
lows = 27.95;
[t1,XX] = ode45(@func_lorenz2,[0 100],[0 1 1.05]);%use the function of ode45 to solve the function
RR3 = XX;
L = min([length(RR1),length(RR2),length(RR3)]);
%先针对p值变大的情况来计算rate
D1 = [RR1(1:L,1) - RR2(1:L,1) , RR1(1:L,2) - RR2(1:L,2) , RR1(1:L,3) - RR2(1:L,3)];
%计算rate
D1d= [diff(RR1(1:L,1) - RR2(1:L,1)) , diff(RR1(1:L,2) - RR2(1:L,2)) , diff(RR1(1:L,3) - RR2(1:L,3))];
%再针对p值变小的情况来计算rate
D2 = [RR1(1:L,1) - RR3(1:L,1) , RR1(1:L,2) - RR3(1:L,2) , RR1(1:L,3) - RR3(1:L,3)];
%计算rate
D2d= [diff(RR1(1:L,1) - RR3(1:L,1)) , diff(RR1(1:L,2) - RR3(1:L,2)) , diff(RR1(1:L,3) - RR3(1:L,3))];
figure;
subplot(211);
plot(D1d(:,1),'m-');hold on
plot(D1d(:,2),'r-');hold on
plot(D1d(:,3),'b-');hold off
title('28.1,[0,1,1.05]');
legend('X','Y','Z');
grid on;
subplot(212);
plot(D2d(:,1),'m-');hold on
plot(D2d(:,2),'r-');hold on
plot(D2d(:,3),'b-');hold off
title('27.9,[0,1,1.05]');
legend('X','Y','Z');
grid on;
%上面是相近的P值来计算最后的rate,下面考虑改变初始值,来计算rate
%上面是相近的P值来计算最后的rate,下面考虑改变初始值,来计算rate
global XX;
global lows;
lows = 28;
[t1,XX] = ode45(@func_lorenz2,[0 100],[0 1 1.05]);%use the function of ode45 to solve the function
RR1 = XX;
[t1,XX] = ode45(@func_lorenz2,[0 100],[0 1 1.06]);%use the function of ode45 to solve the function
RR2 = XX;
[t1,XX] = ode45(@func_lorenz2,[0 100],[0 1 1.04]);%use the function of ode45 to solve the function
RR3 = XX;
L = min([length(RR1),length(RR2),length(RR3)]);
%先针对p值变大的情况来计算rate
D1 = [RR1(1:L,1) - RR2(1:L,1) , RR1(1:L,2) - RR2(1:L,2) , RR1(1:L,3) - RR2(1:L,3)];
%计算rate
D1d= [diff(RR1(1:L,1) - RR2(1:L,1)) , diff(RR1(1:L,2) - RR2(1:L,2)) , diff(RR1(1:L,3) - RR2(1:L,3))];
%再针对p值变小的情况来计算rate
D2 = [RR1(1:L,1) - RR3(1:L,1) , RR1(1:L,2) - RR3(1:L,2) , RR1(1:L,3) - RR3(1:L,3)];
%计算rate
D2d= [diff(RR1(1:L,1) - RR3(1:L,1)) , diff(RR1(1:L,2) - RR3(1:L,2)) , diff(RR1(1:L,3) - RR3(1:L,3))];
figure;
subplot(211);
plot(D1d(:,1),'m-');hold on
plot(D1d(:,2),'r-');hold on
plot(D1d(:,3),'b-');hold off
title('28,[0,1,1.06]');
legend('X','Y','Z');
grid on;
subplot(212);
plot(D2d(:,1),'m-');hold on
plot(D2d(:,2),'r-');hold on
plot(D2d(:,3),'b-');hold off
title('28,[0,1,1.04]');
legend('X','Y','Z');
grid on;
07_002m4.算法理论概述
洛伦兹混沌系统是一种非线性动力系统,最初由爱德华·洛伦兹(Edward Lorenz)于1963年引入,它的简单方程组引发了混沌理论的开创性研究。该系统是混沌现象的典型范例,展示了复杂、不可预测的行为,即使在简单的数学方程下也可以观察到这种行为。
原理:
洛伦兹混沌系统由三个耦合的一阶常微分方程组组成,这三个方程描述了三个状态变量(或者说是维度)之间的关系。这些状态变量表示系统在空间中的位置,从而形成一个三维相空间,该相空间中的轨迹表现出异常的复杂性和混沌特性。
洛伦兹方程组描述如下:

其中,x、y 和 z 是状态变量,t是时间,而 \sigmaσ、\rhoρ 和 \betaβ 则是系统的参数。这些参数的取值会影响洛伦兹系统的动态行为。
系统特点:
- 敏感依赖于初始条件: 洛伦兹系统展现出敏感依赖于初始条件的特点,即微小的初始条件变化可能导致长时间内的轨迹发生巨大的分离。
- 奇异吸引子: 洛伦兹系统的相空间中,轨迹围绕着一个被称为“奇异吸引子”的复杂结构。这个吸引子是一个分形结构,展现了无规则且不可重复的形态。
- 周期性和混沌性共存: 洛伦兹系统在参数空间内可以存在周期性行为和混沌行为,这种现象被称为“周期倍增路线到混沌”。
混沌的产生原理: 洛伦兹混沌系统的混沌行为来源于非线性项的存在。当参数取值在一定范围内,非线性项的影响会导致相空间中的轨迹错综复杂地交织在一起,这使得系统的演化变得高度不可预测。
洛伦兹混沌系统是混沌现象的经典范例,它揭示了非线性系统的复杂行为和对初始条件的敏感性。通过简单的数学方程,洛伦兹系统展现出了无法预测的、高度不稳定的轨迹,这一发现在混沌理论的发展中具有重要地位,深刻影响了许多领域,包括天气预测、物理学、生物学等。
5.算法完整程序工程
OOOOO
OOO文章来源:https://www.toymoban.com/news/detail-667968.html
O文章来源地址https://www.toymoban.com/news/detail-667968.html
到了这里,关于基于matlab的lorenz混沌系统仿真与分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!