目录
01背包
问题描述:
简单描述就是:
解析:
递推公式:
dp数组的初始化:
遍历顺序:
图解:
实现代码:
dp数组初始化:
遍历:
优化:
原理:
递推公式:
遍历顺序:
实现代码:
初始化:
遍历:
完全背包
问题描述:
解析:
实现代码:
01背包
问题描述:
01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2至Wn,与之相对应的价值为P1,P2至Pn。01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品,每种物品有且只有一个,并且有权值和体积两个属性。在01背包问题中,因为每种物品只有一个,对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中,则不需要处理。如果选择将其放入背包中,由于不清楚之前放入的物品占据了多大的空间,需要枚举将这个物品放入背包后可能占据背包空间的所有情况。(来源:百度百科)
简单描述就是:
有N件物品和一个容量为M的背包。第 i 件物品的体积(也可以是重量等)是w[ i ],价值是v[ i ]。求解将哪些物品装入背包可使价值总和最大。
解析:
递推公式:
如果没接触过背包问题的话,应该首先会想到的是暴力写法,也就是回溯算法,把所有的情况都找出来,然后通过不断的比较和更新求出最大价值,显然这种方法的需要的时间是很长的,时间复杂度是2的n次方。
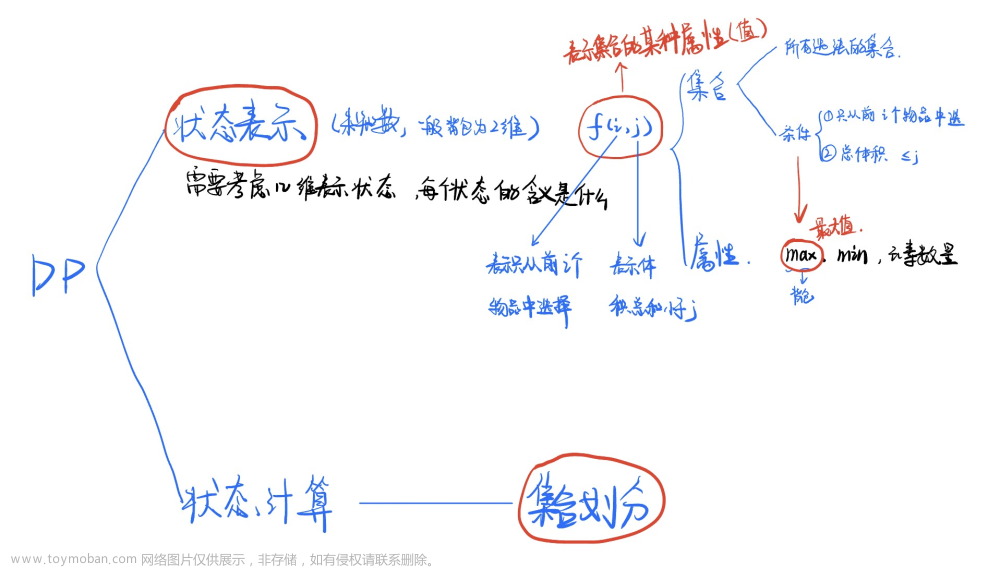
所以我们就要用动态规划,最重要的就是理解dp数组的含义,若是dp[ i ][ j ]数组不理解,后面的就更不可能理解了,dp[ i ][ j ]数组的含义就是在0 ~ i的物品中选取放入 j 容量的背包得到的最大价值。注意这里选取不是全都放进去的意思,是选择其中的任意几个放进去,一个物品是有两种状态的,已放入和未放入,就是对于前 i 个物品进行放入或未放入的选择后得到的最大价值。
现在我们对于前 i 个物品进行选择求出最大价值,一个物品有两个状态,写出递推公式:
i 不放入:dp[ i ][ j ] = dp[ i - 1 ][ j ]
i 确定放入:dp[ i ][ j ] = dp[ i - 1 ][ j - w[ i ] ] + v[ i ]
求最大:max(dp[ i - 1 ][ j ], dp[ i - 1 ][ j - w[ i ] ] + v[ i ])
不放入的递推公式好理解,就是已经确定第 i 件不放入了,那我们的最大价值就等于在前 i - 1的中选取放入 j 容量背包的最大价值。
确定放入的递推公式不好理解,因为我们这里已经确定第 i 件放入,那就说明 i 一定会放入,我们要把背包留出第 i 件的空间,所有我们就对于前 i - 1 件选取放入 j - w[ i ] 的容量中,这里减去的 w[ i ] 就是为第 i 件留出的空间,然后加上第 i 件的价值,就求出了确定放入的最大价值。
然后我们在不放入和放入之中获得他们的最大值就得到了dp[ i ][ j ],下面给出完整递推公式:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);dp数组的初始化:
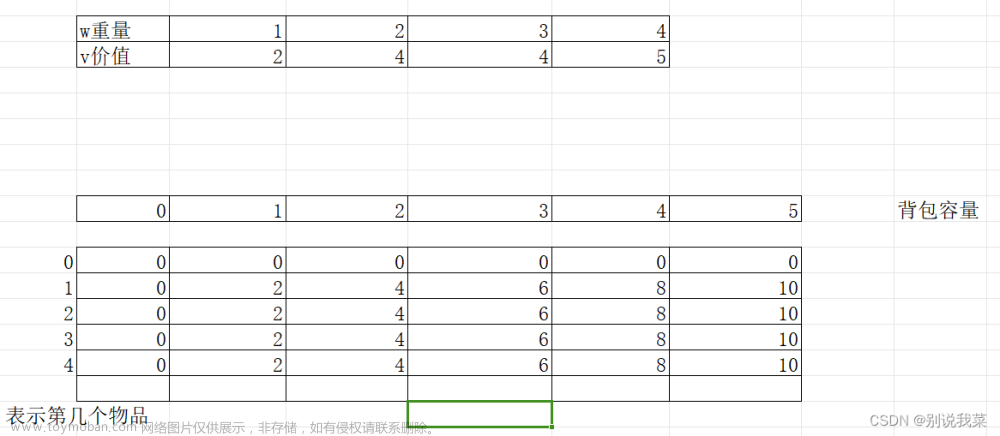
通过递推公式,我们可以发现dp[ i ][ j ]在二维数组中就是由其上面dp[ i - 1 ][ j ]和左上角dp[ i - 1 ][ j - w[ i ] ]的值求得,所以我们初始化dp数组第一行和第一列就可以。第一列背包空间为0,全部初始化为 0 ,第一行根据第 0 个物品的体积和背包大小比较来初始化即可。
遍历顺序:
其实先遍历背包或物品都是可以的,无非是一个以行遍历,一个以列遍历,通过模拟发现都是可以求出对应值的,一般先便利物品,方便理解。
图解:
给出初始化和代码执行流程的模拟,配合图来理解会更加深刻。

实现代码:
这里只给出主要代码,根据具体问题自行添加其他代码即可。
dp数组初始化:
// 二维数组,n 物品个数
vector<vector<int>> dp(n, vector<int>(bagw + 1, 0));
// 初始化
for (int j = w[0]; j <= bagw; j++)
{
dp[0][j] = v[0];
}
遍历:
// n 物品个数 ,m 背包大小
// 遍历物品
for (int i = 1; i < n; i++)
{
//遍历背包
for (int j = 0; j <= m; j++)
{
if (j < w[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}优化:
原理:
其实就是把二维数组变为一维数组,我们在二维遍历时,会发现在其求的值仅仅是用了上一层的数,而用不到其他的数字,所以我们就可以只维护一层数组,不断的更新本层的数来达到降维的作用。所以递推的公式和遍历的顺序就要发生改变。
递推公式:
i 不放入:dp[ j ] = dp[ j ]
i 确定放入:dp[ j ] = dp[ j - w[ i ] ] + v[ i ]
求最大:max(dp[ j ], dp[ j - w[ i ] ] + v[ i ])
遍历顺序:
首先,优化后,我们只能先遍历物品,而不能先背包,毕竟我们模拟的是二维中先遍历背包的一层数组。
其次,在遍历内层背包时,我们只能倒序遍历,从大向小,从后向前,因为我们在二维中递推公式用的是左上角和上面的数求得,若从前向后遍历,根据递推公式,我们不断的更新了左侧的数,会使后面的数得到的是更新后的数,而不是原本上一层的数,而倒序就可以避免这个问题。
简单来说就是二维数组情况下,使用 i - 1 行的已知最大价值来推断,是左上角和上面的数据,但是换成一维数组的话,左上角的数据就是左边的数据,因此,只能从右边开始遍历背包的容量,如果从左边开始遍历的话,就会导致重复计算。
实现代码:
初始化:
// 初始化
vector<int> dp(n + 1, 0);遍历:
两种方法一样,第一种和二维对应方便理解,而第二种比较简洁,因为一维用的是用一个数组,我们不去改变数的值就表示把自己赋值给自己的操作了。
// n 物品个数 ,m 背包大小
// 遍历物品
for (int i = 1; i <= n; i++)
{
for (int j = m; j >= 0; j--)
{
if (j >= w[i]) dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
else dp[j] = dp[j];
}
}// n 物品个数 ,m 背包大小
// 遍历物品
for (int i = 0; i < n; i++)
{
// 遍历背包
for (int j = m; j >= w[i]; j--)
{
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
完全背包
问题描述:
完全背包就是 01 背包的物品可以用多次。文章来源:https://www.toymoban.com/news/detail-668208.html
解析:
写 01 背包代码的时候说了物品从前向后遍历会导致物品多次计算。而多重背包就是要多次取同一个物品,正好就对上了,所以我们的代码就很明确了。文章来源地址https://www.toymoban.com/news/detail-668208.html
实现代码:
// n 物品个数 ,m 背包大小
// 遍历物品
for (int i = 0; i < n; i++)
{
// 遍历背包
for (int j = w[i]; j <= m; j++)
{
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
到了这里,关于动态规划:0-1背包、完全背包问题 | 详细原理解释 | 代码及优化(C++)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!