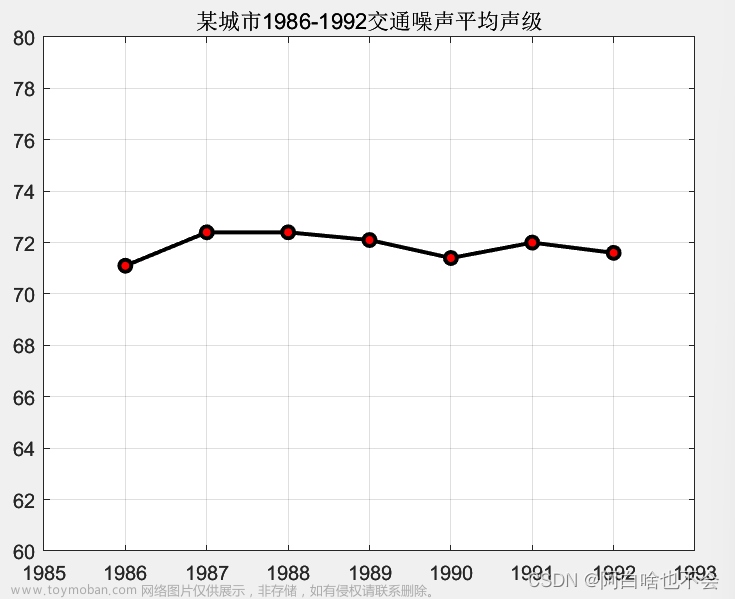
数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成

生成效果

数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成,MCMC,马尔科夫蒙特卡洛模拟,数据生成

基本描述

1.MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成；
2.马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo)，简称MCMC，MCMC算法的核心思想是我们已知一个概率密度函数，需要从这个概率分布中采样，来分析这个分布的一些统计特性。

模型描述

马尔科夫蒙特卡洛模拟（Markov Monte Carlo simulation）是一种基于马尔科夫链的随机模拟方法，用于生成服从某个特定分布的数据样本。下面是使用马尔科夫蒙特卡洛模拟生成数据的一般过程：
定义状态空间：确定数据的可能取值范围，可以是一个离散的状态空间或者一个连续的状态空间。
构建转移矩阵：根据问题的特点，确定状态之间的转移概率。转移矩阵描述了从一个状态转移到另一个状态的概率。
初始化状态：从状态空间中选择一个初始状态。
进行模拟：根据转移矩阵和当前状态，按照一定的概率规则转移到下一个状态。重复这个过程多次，直到达到所需的样本数量。
生成样本：记录每个状态的取值，得到生成的数据样本。

程序设计

完整程序和数据获取方式：私信博主回复MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成。


burn_in = 1000;      % Number of burn-in iterations
proposal_std = 0.9;  % Standard deviation of proposal distribution
% Initialize the chain
current_state = mean(original_data); % Start from the mean of the original data
% Preallocate array for storing generated samples
synthetic_data = zeros(1, num_samples);
% Metropolis-Hastings algorithm
for t = 1:num_samples + burn_in
% Propose a new state from a Gaussian distribution
proposed_state = current_state + proposal_std * randn();
% Calculate acceptance ratio
current_likelihood = normpdf(current_state, target_mean, target_std);
proposed_likelihood = normpdf(proposed_state, target_mean, target_std);
acceptance_ratio = min(1, proposed_likelihood / current_likelihood);
% Accept or reject the proposed state
if rand() < acceptance_ratio
current_state = proposed_state;

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229文章来源地址https://www.toymoban.com/news/detail-668243.html

到了这里，关于数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！